2024-2025学年四川省天立集团高二（上）期中数学试卷（含答案）

这是一份2024-2025学年四川省天立集团高二（上）期中数学试卷（含答案），共9页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
1.已知直线l1：2x+y−2=0，l2：ax+4y+1=0，若l1//l2，则a的值为( )
A. 8B. 2C. −12D. −2
2.若a+b=(−2,−1,2)，a−b=(4,−3,−2)，则a⋅b等于( )
A. −5B. −1C. 5D. 7
3.一组数据按从小到大的顺序排列为2，3，4，x，7，8(其中x≠7)，若该组数据的中位数是极差的56，则该组数据的60%分位数是( )
A. 4B. 4.5C. 5D. 6
4.已知圆C：(x−3)2+(y−3)2=72，若直线x+y−m=0垂直于圆C的一条直径，且经过这条直径的一个三等分点，则m=( )
A. 2或10B. 4或8C. 4或6D. 2或4
5.椭圆x225+y216=1的左、右焦点分别为F1、F2，则椭圆上满足PF1⊥PF2的点P( )
A. 有2个B. 有4个C. 不一定存在D. 一定不存在
6.P为⊙C：x2+y2−2x−2y=0上一点，Q为直线l：x−y−4=0上一点，则线段PQ长度的最小值( )
A. 2B. 2 33C. 2 63D. 2 2
7.若半径为r的小球可以在棱长均为8的四棱锥内部自由转动，则r的最大值为( )
A. 3+1B. 2( 3+1)C. 2( 6− 2)D. 2( 6−1)
8.我国著名数学家华罗庚曾说“数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休.”事实上，很多代数问题可以都转化为几何问题加以解决，列如，与 (x−a)2+(y−b)2相关的代数问题，可以转化为点(x,y)与点(a,b)之间的距离的几何问题.已知点M(x1,y1)在直线l1：y=x+2，点N(x2,y2)在直线l2：y=x上，且MN⊥l1，结合上述观点， x12+(y1−4)2+ (x2−5)2+y22的最小值为( )
A. 7 22B. 11 22C. 41− 2D. 5
二、多选题：本题共3小题，共18分。在每小题给出的选项中，有多项符合题目要求。
9.下列命题正确的是( )
A. 若事件A，B，C两两互斥，则P(A∪B∪C)=P(A)+P(B)+P(C)成立
B. 若事件A，B，C两两独立，则P(ABC)=P(A)P(B)P(C)成立
C. 若事件A，B相互独立，则A−与B−也相互独立
D. 若P(A)>0，P(B)>0，则事件A，B相互独立与A，B互斥不能同时成立
10.设直线系M：xcsθ+(y−2)sinθ=1(0≤θ≤2π)，则下面四个命题正确的是( )
A. 点(0,2)到M中的所有直线的距离恒为定值
B. 存在定点P不在M中的任意一条直线上
C. 对于任意整数n(n≥3)，存在正n边形，其所有边均在M中的直线上
D. M中的直线所能围成的三角形面积都相等
11.如图，正方体ABCD−A′B′C′D′的棱长为4，M是侧面ADD′A′上的一个动点(含边界)，点P在棱CC′上，且|PC′|=1，则下列结论正确的有( )
A. 沿正方体的表面从点A到点P的最短距离为 73
B. 保持PM与BD′垂直时，点M的运动轨迹长度为3 2
C. 若保持|PM|=2 5，则点M的运动轨迹长度4π3
D. 平面AD′P截正方体ABCD−A′B′C′D′所得截面为等腰梯形
三、填空题：本题共3小题，每小题5分，共15分。
12.已知空间的一组基底为{a,b,c}，m=a+3b−c，n=xa−2yb+2c，且满足m//n，则xy= ______．
13.已知某三棱台的高为2 5，上、下底面分别为边长为4 3和6 3的正三角形，若该三棱台的各顶点都在球O的球面上，则球O的表面积为______．
14.已知实数a，b满足a2+b2=2a−2b，则3−ba+1的最大值为______．
四、解答题：本题共5小题，共148分。解答应写出文字说明，证明过程或演算步骤。
15.(本小题12分)
如图，已知三棱柱ABC−A1B1C1中，AC⊥BC，AA1⊥平面ABC，CC1=2AC=2BC=4，M为AB边上的动点．
(1)当AM=BM时，求证：CM⊥平面ABB1A1；
(2)求三棱锥C−A1B1M的体积．
16.(本小题100分)
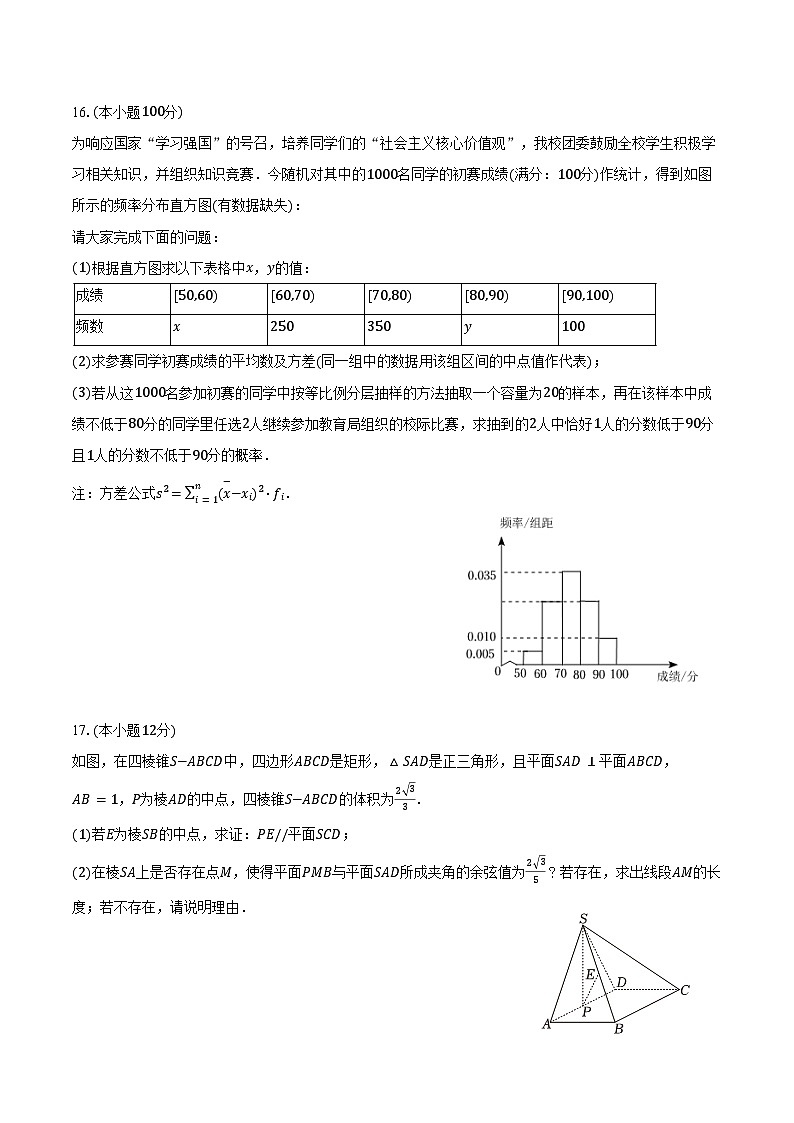
为响应国家“学习强国”的号召，培养同学们的“社会主义核心价值观”，我校团委鼓励全校学生积极学习相关知识，并组织知识竞赛．今随机对其中的1000名同学的初赛成绩(满分：100分)作统计，得到如图所示的频率分布直方图(有数据缺失)：
请大家完成下面的问题：
(1)根据直方图求以下表格中x，y的值：
(2)求参赛同学初赛成绩的平均数及方差(同一组中的数据用该组区间的中点值作代表)；
(3)若从这1000名参加初赛的同学中按等比例分层抽样的方法抽取一个容量为20的样本，再在该样本中成绩不低于80分的同学里任选2人继续参加教育局组织的校际比赛，求抽到的2人中恰好1人的分数低于90分且1人的分数不低于90分的概率．
注：方差公式s2=i=1n(x−−xi)2⋅fi．
17.(本小题12分)
如图，在四棱锥S−ABCD中，四边形ABCD是矩形，△SAD是正三角形，且平面SAD⊥平面ABCD，AB=1，P为棱AD的中点，四棱锥S−ABCD的体积为2 33．
(1)若E为棱SB的中点，求证：PE//平面SCD；
(2)在棱SA上是否存在点M，使得平面PMB与平面SAD所成夹角的余弦值为2 35？若存在，求出线段AM的长度；若不存在，请说明理由．
18.(本小题12分)
蝴蝶定理因其美妙的构图，像是一只翩翩起舞的蝴蝶，一代代数学名家蜂拥而证，正所谓花若芬芳蜂蝶自来.如图，已知圆M的方程为x2+(y−b)2=r2，直线x=my与圆M交于C(x1,y1)，D(x2,y2)，直线x=ny与圆M交于E(x3,y3)，F(x4,y4).原点O在圆M内.设CF交x轴于点P，ED交x轴于点Q．
(1)当b=0，r= 5，m=−12，n=2时，分别求线段OP和OQ的长度；
(2)①求证：y1+y2y1y2=y3+y4y3y4．
②猜想|OP|和|OQ|的大小关系，并证明．
19.(本小题12分)
已知直线l：ax+by+c=0和点P(x0,y0)，点P到直线l的有向距离d(P,l)用如下方法规定：若b≠0，d(P,l)=|b||ax0+by0+c|b a2+b2，若b=0，d(P,l)=ax0+ca．
(1)已知直线l1：3x−4y+12=0，直线l2：2x+3=0，求原点O到直线l1，l2的有向距离d(O,l1)，d(O,l2)；
(2)已知点A(2,1)和点B(3,−1)，是否存在通过点A的直线l3，使得d(B,l3)=2？如果存在，求出所有这样的直线l3，如果不存在，说明理由；
(3)设直线l4：xcsα+2ysinα−2=0，问是否存在实数t>0，使得对任意的参数α都有：点F1(−t,0)，F2(t,0)到l4的有向距离d(F1,l4)，d(F2,l4)满足d(F1,l4)⋅d(F2,l4)=1？如果满足，求出所有满足条件的实数t；如果不存在，请说明理由．
参考答案
1.A
2.A
3.D
4.A
5.D
6.A
7.C
8.D
9.ACD
10.ABC
11.BCD
12.−6
13.144π
14.7
15.解：(1)证明：∵AA1⊥平面ABC，又CM⊂平面ABC，
∴AA1⊥CM，
∵AC=BC，AM=BM，
∴CM⊥AB，又AA1⊥CM，且AA1∩AB=A，
∴CM⊥平面ABB1A1；
(2)∵CC1=2AC=2BC=4，AC⊥BC，
∴AB= AC2+BC2=2 2，
又由(1)知CM⊥平面ABB1A1，
∴点C到平面A1B1M距离为CM=AB2= 2，
∵三棱柱ABC−A1B1C1中，AA1⊥平面ABC，
∴四边形ABB1A1为矩形，
∴当M点在AB上运动时，△A1B1M的面积是定值，
又AA1=CC1=4，A1B1=AB=2 2，
∴S△A1B1M=12A1B1⋅A1A=12×2 2×4=4 2，
∴VC−A1B1M=13×4 2× 2=83．
16.解：(1)由直方图可知成绩在[50,60)的频率为0.005×10=0.05，
所以成绩在[50,60)的频数x=1000×0.05=50，
则成绩在[50,60)的频数y=1000−50−250−350−100=250；
(2)设[60,70)分组的频率/组距为a，则a=2501000×110=0.025，
平均数x−=11000(50×55+250×65+75×350+85×250+95×100)=76，
S2=(76−55)2×0.05+(76−65)2×0.25+(76−75)2×0.35+(76−85)2×0.25+(76−95)2×0.1=109；
(3)从这1000名参加初赛的同学中按等比例分层抽样的方法抽取一个容量为20的样本，
则抽样比为201000=150，
成绩在[80,90)内的有250人，故抽取5人，
成绩在[90,100)的有100人，故抽取2人，
所以从这7人中任取两人，恰好1人的分数低于90分且1人的分数不低于90分的概率P=C51C21C72=1021．
17.证明：(1)取SC的中点F，连接EF，FD，
如图所示：

由于点E、F分别为SB、SC的中点，
所以EF/​/BC，EF=12BC，
由于底面四边形ABCD为矩形，P为棱AD的中点，
所以PD/​/BC，PD=12BC，
所以EF/​/PD，EF=PD，
故四边形PDFE为平行四边形，所以PE//FD，
由于FD⊂平面SCD，PE⊈平面SCD，
所以PE/​/平面SCD．
解：(2)假设在棱SA上存在点M满足题意，
在等边三角形SAD中，点P为AD的中点，所以SP⊥AD，
由于平面SAD⊥平面ABCD，
SP⊂平面SAD，
所以SP⊥平面ABCD，
则SP为四棱锥S−ABCD的高，
设AD=m，SP= 32m，S矩形ABCD=m，
V四棱锥S−ABCD=13S矩形ABCD⋅SP=13m× 32m=2 33，解得m=2；
以点P为原点，PA，AB，PS的方向为x轴，y轴和z轴建立空间直角坐标系，
如图所示：

则P(0,0,0)，A(1,0,0)，B(1,1,0)，S(0,0, 3)，
所以PA=(1,0,0)，PB=(1,1,0)，AS=(−1,0, 3)，
设AM=λAS=(−λ,0, 3λ)，(0≤λ≤1)，
所以PM=PA+AM=(1−λ,0, 3λ)，
设平面PMB的法向量为n1=(x,y,z)，
故n1⋅PM=(1−λ)x+ 3λz=0 n1⋅PB=x+y=0，解得n1=( 3λ,− 3λ,λ−1)，
易知平面SAD的法向量为|n2|=(0,1,0)，
所以|cs|=|n1⋅n2||n1||n2|=|− 3λ| 7λ2−2λ+1=2 35，
由于0≤λ≤1，所以λ=23，
故存在点M，且AM=43满足题意．
18.解：(1)当b=0，r= 5，m=−12，n=2时，
圆M：x2+y2=5，
直线CD：x=−12y，由x2+y2=5x=−12y⇒x=−1y=2或x=1y=−2，故C(−1,2)，D(1,−2)；
直线EF：x=2y，由x2+y2=5x=2y⇒x=−2y=−1或x=2y=1，故E(2,1)，F(−2,−1)．
所以直线CF：y+12+1=x+2−1+2，令y=0，得x=−53，即P(−53,0)；
直线ED：y−1−2−1=x−21−2，令y=0，得x=53，即Q(53,0)．
所以|OP|=|OQ|=53．
(2)①证明：由题意：b20，即t= 3，
当sinα≠0时，直线l4：xcsα+2ysinα−2=0，
得d(F1,l4)=|2sinα||−tcsα−2|(2sinα) cs2α+4sin2α,d(F2,l4)=|2sinα||tcsα−2|(2sinα) cs2α+4sin2a，
由d(F1,l4)⋅d(F2,l4)=|(tcsα−2)(−tcsα−2)|cs2α+4sin2α=1，
即|4−t2cs2α|=cs2α+4sin2α=4−3cs2α，4−t2cs2α=4−3cs2α或4−t2cs2α=3cs2α−4，解得t2=3或(t2+3)cs2α=8，
由题意对任意的参数α都有d(F1,l4)⋅d(F2,l4)=1恒成立，所以t= 3，
综上所述，存在实数t>0满足题目条件，即t= 3． 成绩
[50,60)
[60,70)
[70,80)
[80,90)
[90,100)
频数
x
250
350
y
100