第07讲 复数的概念-【寒假提升课】2025年高一数学寒假提升试题（人教A版2019）

这是一份第07讲 复数的概念-【寒假提升课】2025年高一数学寒假提升试题（人教A版2019），文件包含第07讲复数的概念原卷版docx、第07讲复数的概念解析版docx等2份试卷配套教学资源，其中试卷共35页， 欢迎下载使用。

知识点1 实数系
（1）实数系的分类
(2)实数的性质
①实数对四则运算是封闭的,即两个实数进行四则运算的结果仍是实数；
②加法与乘法满足交换律、结合律,乘法对加法满足分配律；
③实数和数轴上的点可以建立一一对应关系.
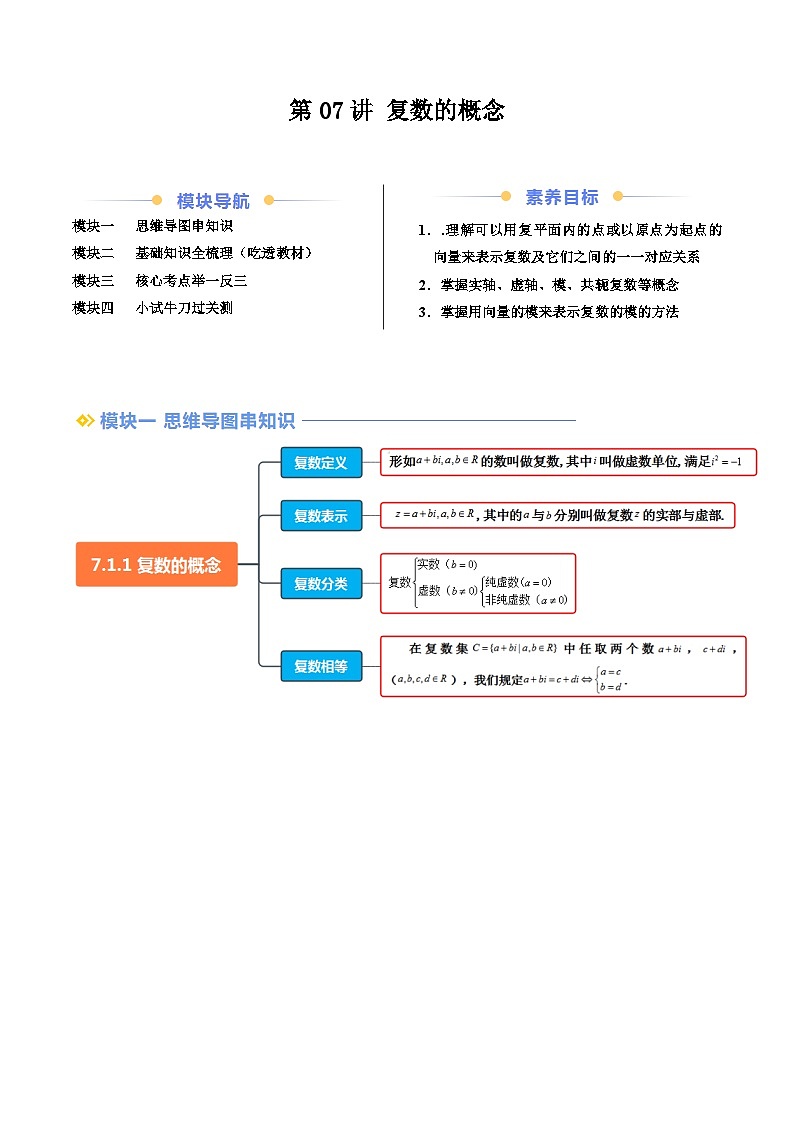
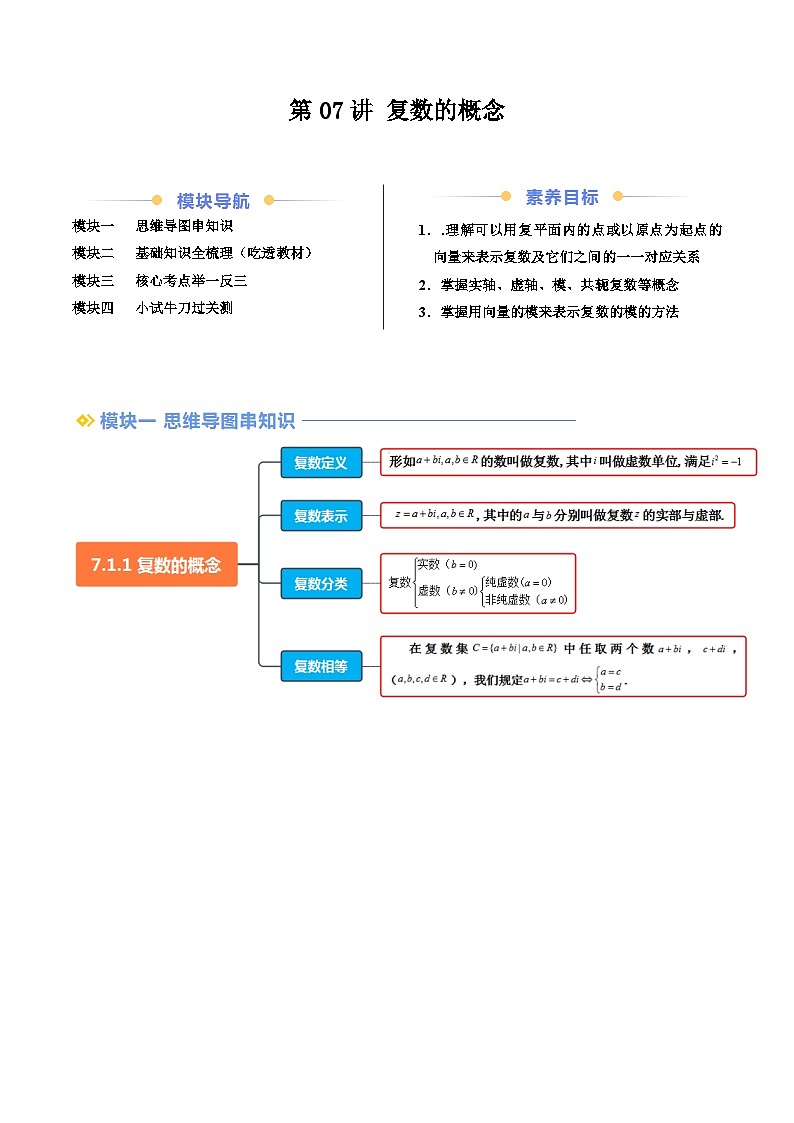
知识点2 复数的概念
（1）复数的引入
为了解决这样的方程在实数系中无解的问题,设想引入一个新数,使得是方程的解,即使得,并且可与实数进行四则运算,且原有的加法与乘法的运算律仍成立.
所以实数系经过扩充后得到的新数集是.
（2）复数的概念
我们把形如的数叫做复数,其中叫做虚数单位,满足.全体复数所构成的集合叫做复数集.
复数的表示:复数通常用字母表示,即,其中的与分别叫做复数的实部与虚部.
（3）复数相等
在复数集中任取两个数，，（），我们规定.
知识点3 复数的分类
对于复数(),当且仅当时,它是实数；当且仅当时,它是实数0；当时,它叫做虚数；当且时,它叫做纯虚数.这样,复数()可以分类如下:
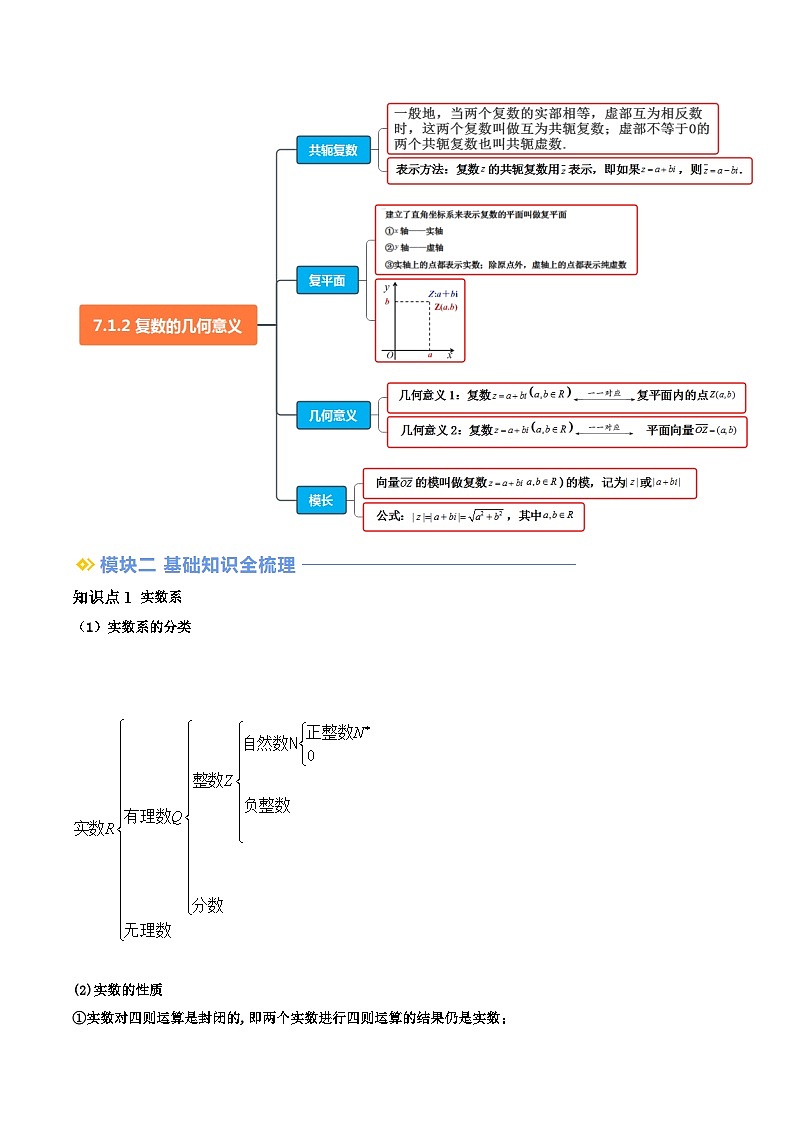
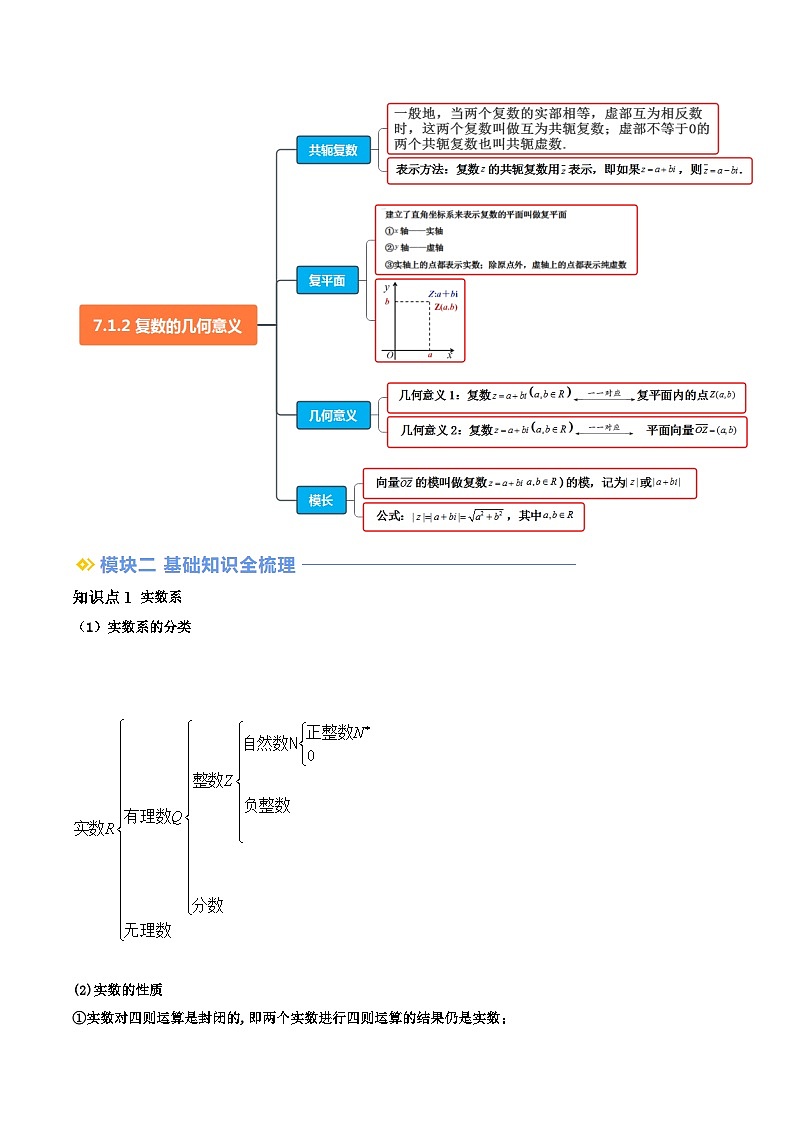
知识点4 复数的几何意义
（1）复数的几何意义——与点对应
复数的几何意义1：复数复平面内的点
（2）复数的几何意义——与向量对应
复数的几何意义2：复数 平面向量
知识点5 复数的模
向量的模叫做复数)的模，记为或
公式：，其中
复数模的几何意义：复数在复平面上对应的点到原点的距离；
特别的，时，复数是一个实数，它的模就等于(的绝对值).
知识点6 共轭复数
（1）定义
一般地，当两个复数的实部相等，虚部互为相反数时，这两个复数叫做互为共轭复数；虚部不等于0的两个共轭复数也叫共轭虚数.
（2）表示方法
表示方法：复数的共轭复数用表示，即如果，则.
考点一：虚单位及其性质
例1．（23-24高一下·全国·课堂例题）计算：① ；②若，则 .
【答案】 -1
【知识点】根据相等条件求参数、虚数单位i及其性质
【分析】①根据规定可得，②设，根据复数相等解方程即可
【详解】根据规定知；
设，
得，或，
所以
故答案为：-1；
【变式1-1】（23-24高一下·山东枣庄·期中） ．
【答案】
【知识点】虚数单位i及其性质
【分析】根据虚数单位的周期性求解.
【详解】,
故答案为：
【变式1-2】（23-24高一下·河北张家口·阶段练习） .
【答案】0
【知识点】虚数单位i及其性质
【分析】利用虚数单位的性质进行计算即可.
【详解】，
故答案为：0.
【变式1-3】（24-25高一上·上海·课堂例题）的平方根为 .
【答案】
【知识点】虚数单位i及其性质
【分析】利用平方根的定义计算即可
【详解】的平方根为，
故答案为：.
考点二：复数的基本概念
例2.（2024高一·全国·专题练习）给出下列四个命题：
①两个复数不能比较大小；
②若实数a与ai对应，则实数集与纯虚数集一一对应；
③纯虚数集相对复数集的补集是虚数集；
④以2为实部的复数有无数个．
其中真命题是 .（填写序号）
【答案】④
【知识点】复数的基本概念
【分析】根据复数的概念一一分析即可.
【详解】①中当这两个复数都是实数时，可以比较大小，故①为假命题；
②若，则ai不是纯虚数，故②为假命题；
③纯虚数集相对复数集的补集不是虚数集，因为复数中还包含实数，则③为假命题；
④对于复数，a有无数个取值，故④为真命题．
故答案为：④.
【变式2-1】（23-24高一下·全国·课后作业）判断题
（1）判断：实数集在复数集中的补集是虚数集.( )
（2）判断：满足的数x只有i.( )
（3）判断：形如的数不一定是纯虚数.( )
（4）判断：两个复数不相等的一个充分条件是它们的虚部不相等.( )
（5）判断：复数由实数、虚数、纯虚数构成.( )
【答案】 正确 错误 正确 正确 错误
【知识点】虚数单位i及其性质、复数的基本概念、求复数的实部与虚部、复数的分类及辨析
【分析】对于（1）（5）：根据复数的相关概念分析判断；对于（2）：根据虚数单位的性质以及复数的乘法分析判断；对于（3）：根据纯虚数的概念分析判断；对于（4）：根据复数相等分析判断.
【详解】对于（1）（5）：因为复数集由实数集、虚数集构成，
即复数分为实数、虚数两个部分，故（5）错误，
即实数集在复数集中的补集是虚数集，故（1）正确；
对于（2）：因为，所以满足的数x有，故（2）错误；
对于（3）：例如，可知为实数，故（3）正确；
对于（4）：因为复数相等的充要条件为：实部相等且虚部相等，
若两个复数的虚部不相等，则这两个复数不相等，
所以个复数不相等的一个充分条件是它们的虚部不相等，故（4）正确；
故答案为：正确；错误；正确；正确；错误.
【变式2-2】（24-25高一上·上海·课前预习）.( )
【答案】错误
【知识点】复数的基本概念
【分析】由复数不能比较大小即可判断.
【详解】因为复数不能比较大小，所以是错误的.
故答案为：错误.
【变式2-3】（24-25高一上·上海·课堂例题）若复数，则、一定都是实数.( )
【答案】正确
【知识点】复数的基本概念
【分析】根据复数的概念即可判断.
【详解】两个实数可以比较大小，但是两个复数，如果不全是实数，它们之间就不能比较大小，只能说相等或不相等.
故判断为：正确.
考点三：复数的实部与虚部
例3.（23-24高一下·全国·课堂例题）分别写出下列各复数的实部与虚部．
(1)；
(2)；
(3)；
(4)；
(5)；
(6)；
(7)；
(8)；
(9)；
(10)；
(11)；
(12)．
【答案】(1)实部为，虚部为
(2)实部为，虚部为
(3)实部为，虚部为
(4)实部为，虚部为
(5)实部为，虚部为
(6)实部为，虚部为
(7)实部为，虚部为
(8)实部为，虚部为
(9)实部为，虚部为
(10)实部为，虚部为
(11)实部为，虚部为
(12)实部为，虚部为
【知识点】求复数的实部与虚部
【分析】根据复数的实部和虚部的概念进行求解.
【详解】（1）的实部为，虚部为
（2）的实部为，虚部为
（3）的实部为，虚部为
（4）实部为，虚部为
（5）的实部为，虚部为
（6）的实部为，虚部为
（7）的实部为，虚部为
（8）的实部为，虚部为
（9）的实部为，虚部为
（10）的实部为，虚部为
（11）的实部为，虚部为
（12）的实部为，虚部为
【变式3-1】（2024高一下·全国·专题练习）复数，则（ ）
A．的实部为B．的虚部为
C．的虚部为D．的虚部为1
【答案】B
【知识点】求复数的实部与虚部
【分析】利用复数的虚部与实部的定义求解.
【详解】复数的实部为，虚部为，
故选：B.
【变式3-2】（23-24高三上·北京·阶段练习）已知复数，则复数的实部为 .
【答案】/
【知识点】特殊角的三角函数值、求复数的实部与虚部
【分析】利用诱导公式及特殊角的三角函数值将复数化简，再判断其实部即可.
【详解】解：
所以复数的实部为；
故答案为：
【变式3-3】（23-24高一·全国·课后作业）的实部等于3，虚部等于4i( )
【答案】错误
【知识点】求复数的实部与虚部
【分析】利用复数的概念即可求解.
【详解】的虚部是4.
故答案为;错误.
考点四：复数相等
例4.（23-24高一下·新疆克孜勒苏·期中）已知为虚数单位，，为实数，若，则（ ）
A．1B．C．5D．
【答案】C
【知识点】复数的相等
【分析】根据复数相等的充要条件可得，即可求解.
【详解】由可得，所以5，
故选：C
【变式4-1】（23-24高一下·湖南·期末）已知x，，则“”是“”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
【答案】A
【知识点】复数的相等、判断命题的充分不必要条件
【分析】利用复数相等的概念，以及条件的变化，再用是否推出思想来判断充分不必要条件.
【详解】当时，显然成立，所以是的充分条件；
当时，，
则是的不必要条件；
故选：A.
【变式4-2】（23-24高一下·广西南宁·期中）若实数，满足，则（ ）
A．B．3C．D．1
【答案】B
【知识点】复数的相等
【分析】根据复数相等的充要条件求出，的值，即可得解.
【详解】因为实数，满足，
所以，则.
故选：B
【变式4-3】（24-25高一上·全国·课后作业）设，，求x，y的值．
【答案】
【知识点】复数的相等
【分析】根据相等复数的条件建立方程组，解之即可求解.
【详解】由题意知，，
由复数相等的定义，得，解得，
所以.
考点五：复数分类
例5.（23-24高二下·吉林辽源）已知复数.
（1）取什么值时，为实数；
（2）取什么值时，为纯虚数.
【答案】（1）（2）
【知识点】复数的分类及辨析、已知复数的类型求参数
【分析】(1) 直接由虚部为0求解m值;(2) 由实部为0且虚部不为0求解m值.
【详解】（1）复数，
若为实数，则，即
（2）若为纯虚数，则，
解得
【点睛】本题主要考查了复数的相关概念，考查了运算能力，属于容易题.
【变式5-1】（多选）（23-24高一下·江苏泰州·期中）对于复数，则下列结论中错误的是（ ）
A．若，则为纯虚数B．若，则
C．若，则为实数D．若，则不是复数
【答案】ABD
【知识点】求复数的实部与虚部、复数的分类及辨析
【分析】A.由判断；B.由复数的实部和虚部判断；C.复数的分类判断；D.由复数的分类判断.
【详解】A.当时，为实数，故错误；
B.若，则，故错误；
C.若，则为实数，故正确；
D.若，则是实数，故错误；
故选：ABD
【变式5-2】（24-25高一上·上海·随堂练习）下列各数中，哪些是实数？哪些是虚数？哪些是纯虚数？
，，，，，.
【答案】答案见解析
【知识点】复数的基本概念、复数的分类及辨析
【分析】根据复数的分类及复数运算分类即可.
【详解】，，是实数；
，，是虚数；
是纯虚数.
【变式5-3】（23-24高一下·全国·课堂例题）指出下列各数中，哪些是实数，哪些是虚数，哪些是纯虚数，为什么？.
【答案】实数为；虚数为；
纯虚数为
【知识点】复数的分类及辨析
【分析】根据复数为实数、虚数和纯虚数的条件，判断出实数、虚数和纯虚数.
【详解】实数为；
虚数为；
纯虚数为.
【变式5-4】（23-24高二下·四川成都·期中）实数m取什么数值时，复数分别是：
(1)实数？
(2)虚数？
(3)纯虚数？
【答案】(1)或
(2)且
(3)
【知识点】复数的分类及辨析、已知复数的类型求参数
【分析】（1）复数为实数，则虚部为零，即可得出答案.
（2）复数为虚数，则虚部为不为零，即可得出答案.
（3）复数为纯虚数，则实部为零，虚部为不为零，即可得出答案.
【详解】（1）当，即或时，复数z是实数；
（2）当，即且时，复数z是虚数；
（3）当，即时，复数z是纯虚数．
【变式5-5】（23-24高一下·安徽池州·阶段练习）已知复数.
(1)若复数是虚数，求实数的值；
(2)若复数是纯虚数，求实数的值.
【答案】(1)；
(2)1.
【知识点】复数的分类及辨析、已知复数的类型求参数
【分析】（1）根据虚数的概念求解即可；
（2）根据纯虚数的概念由虚部不为0，实部为0建立关系式求解即可.
【详解】（1）因为是虚数，
所以，解得，
（2）因为是纯虚数，
所以，解得.
考点六：复数的坐标表示
例6.（23-24高一下·山东青岛·期中）在复平面内，复数对应的点为，复数对应的点为，则对应的复数为（ ）
A．B．C．D．
【答案】B
【知识点】复数的坐标表示
【分析】利用向量减法法则得到，求出对应的复数.
【详解】由题意得，故对应的复数为.
故选：B
【变式6-1】（23-24高一下·山西太原·期中）在复平面内，复数对应的点的坐标是（ ）
A．B．C．D．
【答案】B
【知识点】复数的坐标表示
【分析】求出复数的实部、虚部可得答案.
【详解】在复平面内，复数对应的点的坐标是.
故选：B.
【变式6-2】（23-24高一下·湖南株洲·期中）复数在复平面直角坐标系中对应的点的坐标为（ ）
A．B．C．D．
【答案】B
【知识点】复数的坐标表示
【分析】根据复数的几何意义直接得出结果.
【详解】由可得其在复平面直角坐标系中对应的点的坐标为.
故选：B
【变式6-3】（24-25高一上·上海·课堂例题）已知，，，，O为复平面的原点，试写出、、，所表示的复数；
【答案】表示的复数为；表示的复数为；表示的复数为；表示的复数为.
【知识点】复数的坐标表示
【分析】由复数集与复平面内的向量所成的集合一一对应的关系直接求解.
【详解】,所以表示的复数为；
同理可得：表示的复数为；表示的复数为；表示的复数为.
考点七：复数的点对应的象限，坐标轴
例7.（23-24高一下·全国·单元测试）若复数所对应的点在第二象限，则的取值范围为 .
【答案】，或.
【知识点】在各象限内点对应复数的特征
【分析】
根据复数所对应的点在第二象限，则得到实部小于零，虚部大于零，解不等式得出结果.
【详解】
因为复数所对应的点在第二象限，
，且，
解得：或.
故答案为：或.
【变式7-1】（23-24高一下·浙江·阶段练习）若复数对应的点在第四象限，则m的值为（ ）
A．B．0C．1D．
【答案】B
【知识点】在各象限内点对应复数的特征、根据复数对应坐标的特点求参数
【分析】由复数表示的点在第四象限，可得实部为正且虚部为负即得.
【详解】由可得，又m为整数，所以.
故选：B.
【变式7-2】（23-24高二下·青海·期末）复数对应的点在第三象限内，则实数m的取值范围是（ ）
A．B．C．D．无解
【答案】C
【知识点】在各象限内点对应复数的特征
【分析】根据复数对应的点在第三象限，让实部虚部均小于0，计算得解.
【详解】解：化简可得：复数，
因为其对应的点在第三象限内，所以，解得．
故选：C.
【变式7-3】（多选）（23-24高一下·浙江湖州·阶段练习）若，则复数在复平面内对应的点可能在（ ）．
A．第一象限B．第二象限C．第三象限D．第四象限
【答案】CD
【知识点】已知角或角的范围确定三角函数式的符号、判断复数对应的点所在的象限、在各象限内点对应复数的特征
【分析】分与两种情况下得到余弦和正弦值的正负，得到答案.
【详解】当时，，故复数在复平面内对应的点在第三象限，
当时，，故复数在复平面内对应的点在第四象限.
故选：CD
考点八：复数的模
例8.（24-25高三上·四川成都·期中）（ ）
A．2B．C．5D．
【答案】D
【知识点】求复数的模
【分析】根据复数模长公式求出答案.
【详解】.
故选：D
【变式8-1】（23-24高二下·云南·期末）已知i为虚数单位，复数，则（ ）
A．1B．3C．5D．7
【答案】C
【知识点】求复数的模
【分析】根据复数的模公式计算即可.
【详解】由，则.
故选：C.
【变式8-2】（24-25高三上·上海·期中）记是虚数单位，设复数且，则复数的虚部为 .
【答案】
【知识点】求复数的实部与虚部、由复数模求参数
【分析】根据条件，利用复数模长的计算公式，即可求解.
【详解】因为，，则，得到，
又，所以，则复数的虚部为，
故答案为：.
【变式8-3】（23-24高一·上海·课堂例题）已知，其中．求的值．
【答案】
【知识点】由复数模求参数
【分析】由已知利用复数模的计算公式列方程求解.
【详解】由，
得，
即，解得.
考点九：根据复数对应的坐标特点求参数
例9.（23-24高一·上海·课堂例题）求实数m的值或取值范围，使得复数在复平面上所对应的点分别位于
(1)实轴上；
(2)虚轴上；
(3)第四象限．
【答案】(1)或
(2)或
(3)
【知识点】根据复数对应坐标的特点求参数
【分析】（1）根据题意可得，运算求解即可；
（2）由求m，代入验证，即可得结果；
（3）由求出m的范围即可.
【详解】（1）由题意可得：，解得或.
（2）由题设，，可得或，
当时，对应点在虚轴上；
当时，对应点在虚轴上；
综上，或.
（3）由题设，可得.
【变式9-1】（2024·四川成都·模拟预测）在复平面内，复数对应的点位于第二象限，则实数a的取值范围为（ ）．
A．B．C．D．
【答案】A
【知识点】根据复数对应坐标的特点求参数
【分析】利用复数的几何意义得出对应不等式即可得结果.
【详解】复数，其对应的点在第二象限，
则，解得．
故选：A
【变式9-2】（23-24高一下·江苏苏州·期中）复数平面内表示复数的点分别满足下列条件：
(1)位于第四象限；
(2)位于第一象限或第三象限；
(3)位于直线上．求实数的取值范围．
【答案】(1)或
(2)或或
(3)
【知识点】根据复数对应坐标的特点求参数、在各象限内点对应复数的特征
【分析】（1）结合复数的几何意义与第四象限的点的特点计算即可得；
（2）结合复数的几何意义与第一象限或第三象限的点的特点计算即可得；
（3）由题意可得，计算即可得.
【详解】（1）由题意，复数在复平面内对应的点为．
当点位于第四象限时，则，即，
故或；
（2）当点位于第一象限或第三象限时，
则，
即，
故或或．
（3）当点位于直线上，则，解得．
【变式9-3】（23-24高一下·上海·期末）当实数为何值时，复数为：
(1)实数；
(2)纯虚数；
(3)对应点在第二象限？
【答案】(1)或；
(2)；
(3)．
【知识点】已知复数的类型求参数、根据复数对应坐标的特点求参数
【分析】（1）结合实数的概念，即可求解；
（2）结合纯虚数的概念，即可求解；
（3）结合复数的几何意义，即可求解．
【详解】（1）复数为实数，则，
所以或.
（2）复数为纯虚数，则，
所以.
（3）复数对应点在第二象限，则，解得，
所以实数的取值范围是.
一、单选题
1．（23-24高二下·云南·期末）已知i为虚数单位，则复数在复平面内对应的点位于（ ）
A．第一象限B．第二象限
C．第三象限D．第四象限
【答案】A
【知识点】判断复数对应的点所在的象限
【分析】根据复数的几何意义求解即可.
【详解】复数在复平面内对应的点为，位于第一象限.
故选：A.
2．（23-24高一下·四川遂宁·阶段练习）复数，下列说法不正确的是（ ）
A．的实部为2B．的虚部为
C．D．
【答案】B
【知识点】求复数的实部与虚部、求复数的模、共轭复数的概念及计算
【分析】根据复数的实部、虚部、共轭复数、模等知识确定正确答案
【详解】因为，所以实部为2，虚部为3，，.
故选：B
3．（23-24高二下·四川达州·期中）已知复数，则复数在复平面内所对应的点Z位于第（ ）象限
A．一B．二C．三D．四
【答案】D
【知识点】复数的坐标表示、判断复数对应的点所在的象限
【分析】由复数的几何意义得复数对应的点的坐标，可求所在象限.
【详解】复数在复平面内所对应的点，位于第四象限.
故选：D.
4．（23-24高一下·北京丰台·期末）设复数，则（ ）
A．1B．C．2D．4
【答案】B
【知识点】求复数的模
【分析】利用复数模的定义计算即得.
【详解】复数，则.
故选：B
5．（24-25高二上·广西南宁·阶段练习）设，则在复平面内对应点位于（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【答案】A
【知识点】共轭复数的概念及计算、判断复数对应的点所在的象限
【分析】由共轭复数，及复数几何意义可得答案.
【详解】因，则，其在复平面内对应的点为，在第一象限.
故选：A
6．（2024高三·全国·专题练习）在复平面内，O为坐标原点，复数4i对应的向量为，将绕点O按逆时针方向旋转后，再将模变为原来的倍，得到向量，则对应的复数的实部是（ ）
A．6B．C．D．
【答案】B
【知识点】求复数的实部与虚部、复数的向量表示
【分析】根据复数的向量表示形式，结合复数的几何意义、复数实部定义进行求解即可.
【详解】因为复数4i对应的向量为，
所以 ，
绕点O逆时针方向旋转后变为，
再将模变为原来的倍，得，对应的复数的实部是，
故选：B
7．（24-25高三上·广东·阶段练习）在复平面内，复数Z绕原点逆时针旋转得，则复数Z的虚部为（ ）
A．B．C．D．
【答案】C
【知识点】求复数的实部与虚部
【分析】利用复数的几何意义求解即可
【详解】对应的点的坐标为顺时针旋转后坐标为对应的虚数为虚部为
故选：C.
8．（2024高二下·云南·学业考试）已知为虚数单位，则复数在复平面内对应的点位于（ ）
A．第一象限B．第二象限
C．第三象限D．第四象限
【答案】C
【知识点】判断复数对应的点所在的象限
【分析】由复数的几何意义求解．
【详解】复数在复平面内对应的点为，它在第三象限，
故选：C
二、多选题
9．（24-25高三上·广东肇庆·阶段练习）已知复数，，则下列结论正确的是（ ）
A．若为纯虚数，则
B．若在复平面内对应的点位于第二象限，则
C．若，则
D．若，则
【答案】BC
【知识点】根据复数对应坐标的特点求参数、共轭复数的概念及计算、求复数的模、已知复数的类型求参数
【分析】对于A，若为纯虚数，则的实部为0，虚部不为0，列出方程求解即可；对于B，若在复平面内对应的点位于第二象限，则实部小于0且虚部大于0，列出不等式求解即可；对于C，若，求出，进而求其共轭复数；对于D，若，求出，咋求模即可.
【详解】对于A，若为纯虚数，即且，则，故A错误；
对于B，若在复平面内对应的点位于第二象限，则解得，即，故B正确；
对于C，若，则，则，故C正确；
对于D，若，则，故D 错误.
故选：BC.
10．（23-24高一下·河南商丘·期中）已知复数，则下列命题正确的是（ ）
A．若为纯虚数，则
B．若为实数，则
C．若在复平面内对应的点在直线上，则
D．在复平面内对应的点可能在第三象限
【答案】AB
【知识点】判断复数对应的点所在的象限、已知复数的类型求参数
【分析】根据复数的分类，即可列出方程或不等式，进而判断A,B;根据复数的几何意义，即可列出方程或不等式，进而可以判断C,D.
【详解】对于A，若为纯虚数，则，解得，A正确；
对于B，若为实数，则，所以，此时，B正确；
对于C，在复平面内对应的点为，
所以，即，解得或，C错误；
对于D，若在复平面内对应的点在第三象限，则无解，
所以在复平面内对应的点不可能在第三象限，D错误.
故选：AB.
三、填空题
11．（2024·甘肃白银·一模）复数的实部与虚部之和为 .
【答案】5
【知识点】求复数的模、求复数的实部与虚部
【分析】根据复数模长可得，即可根据虚部和实部定义求解.
【详解】由题意得，所以复数的实部与虚部之和为5.
故答案为：5
12．（2024·福建泉州·模拟预测）已知幂函数的图象过点，则复数（其中i为虚数单位）的模的大小= ．
【答案】
【知识点】求复数的模、求幂函数的解析式、求幂函数的值
【分析】设出，代入，求出解析式，计算出，求出，计算出模长.
【详解】设幂函数，因为函数图象过点，
所以，解得，所以，
所以，
，
.
故答案为：．
四、解答题
13．（23-24高一·上海·课堂例题）当复数z满足下列条件时，分别指出z在复平面上所对应的点Z的位置：
(1)z是正实数；
(2)z是负实数；
(3)z是实部小于零、虚部大于零的虚数；
(4)z是虚部小于零的纯虚数．
【答案】(1)，此时对应的点在实轴的正半轴上
(2)，此时对应的点在实轴的负半轴上
(3)，此时对应的点在第二象限
(4)，此时对应的点在虚轴的负半轴上
【知识点】判断复数对应的点所在的象限、求复数的实部与虚部
【分析】根据复数的分类、几何意义求出实部、虚部满足的条件可得答案.
【详解】（1）设，
若是正实数，则，
此时对应的点在实轴的正半轴上；
（2）设，
若是负实数，则，
此时对应的点在实轴的负半轴上；
（3）设，
若是实部小于零、虚部大于零的虚数，
则，此时对应的点在第二象限；
（4）设，
若是虚部小于零的纯虚数，
则，此时对应的点在虚轴的负半轴上.
14．（23-24高一下·甘肃临夏·期末）在复平面内，A，B，C三点对应的复数分别为1，4＋4i．－2＋4i．
(1)求向量对应的复数；
(2)求的面积．
【答案】(1)
(2)12
【知识点】复数的向量表示、坐标计算向量的模
【分析】（1）由复数的几何意义求解即可；
（2）计算向量的模长，判断出为等腰三角形，求解其面积即可.
【详解】（1）对应的复数为．
对应的复数为．
对应的复数为；
（2）因为，，，所以AB=AC，
所以为等腰三角形．
所以．
15．（23-24高一下·海南省直辖县级单位·阶段练习）复数，其中.
(1)若为实数，求a的值；
(2)若为纯虚数，求a的值；
(3)若在复平面内表示的点位于第四象限，求a的取值范围．
【答案】(1)或
(2)
(3)
【知识点】复数的分类及辨析、已知复数的类型求参数、在各象限内点对应复数的特征、根据复数对应坐标的特点求参数
【分析】（1）若为实数，可知虚部为0，列式求解即可；
（2）若为纯虚数，可知虚部不为0，实部为0，列式求解即可；
（3）由题意可知虚部小于0，实部大于0，列式求解即可.
【详解】（1）若为实数，则，解得或．
（2）若为纯虚数，则，解得．
（3）若复数在复平面内对应的点位于第四象限，
则，解得．
即a的取值范围为
16．（23-24高一下·内蒙古通辽·期中）已知复数，求满足下列条件的实数m的值或取值范围.
(1)复数z与复数相等；
(2)复数z与复数互为共轭复数；
(3)复数z在复平面内对应的点在实轴上方.
【答案】(1)
(2)
(3)
【知识点】复数的相等、共轭复数的概念及计算、根据复数对应坐标的特点求参数
【分析】（1）（2）（3）根据复数相等的充要条件,共轭复数，几何意义求解即可.
【详解】（1）根据复数相等的充要条件，得，解得.
（2）根据共轭复数的定义，得，解得.
（3）由题意，知，解得或，
故实数m的取值范围为.
模块一 思维导图串知识
模块二 基础知识全梳理（吃透教材）
模块三 核心考点举一反三
模块四 小试牛刀过关测
1．.理解可以用复平面内的点或以原点为起点的向量来表示复数及它们之间的一一对应关系
2．掌握实轴、虚轴、模、共轭复数等概念
3．掌握用向量的模来表示复数的模的方法