第09讲 基本立体图形-【寒假提升课】2025年高一数学寒假提升试题（人教A版2019）

这是一份第09讲 基本立体图形-【寒假提升课】2025年高一数学寒假提升试题（人教A版2019），文件包含第09讲基本立体图形原卷版docx、第09讲基本立体图形解析版docx等2份试卷配套教学资源，其中试卷共52页， 欢迎下载使用。

知识点 1 空间几何体的相关概念
（1）空间几何体
如果只考虑物体的形状和大小，而不考虑其它因素，那么这些由物体抽象出来的空间图形就叫做空间几何体.
（2）多面体
由若干平面多边形围成的几何体叫做多面体,围成多面体的各个多边形叫做多面体的面；
相邻两个面的公共边叫做多面体的棱；棱与棱的公共点叫做多面体的顶点.
（3）旋转体
由一个平面图形绕它所在的平面内的一条定直线旋转所形成的封闭几何体叫做旋转体.
知识点2 棱柱
（1）棱柱的定义
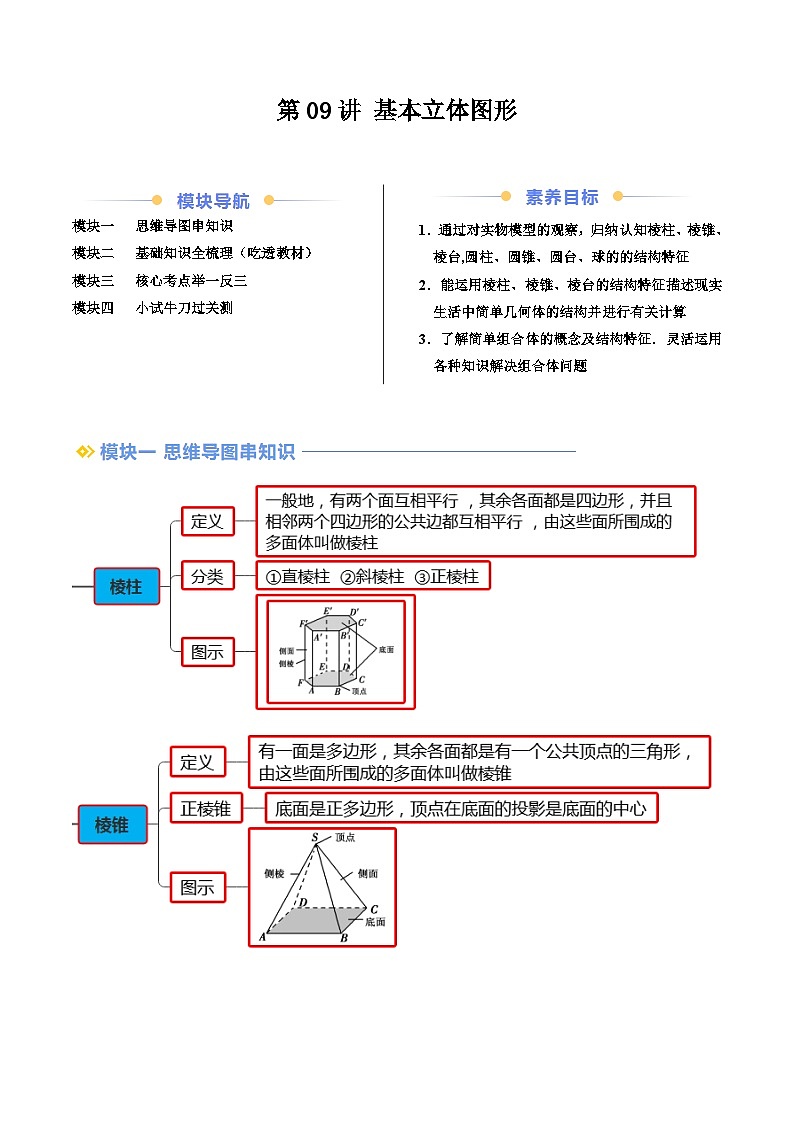
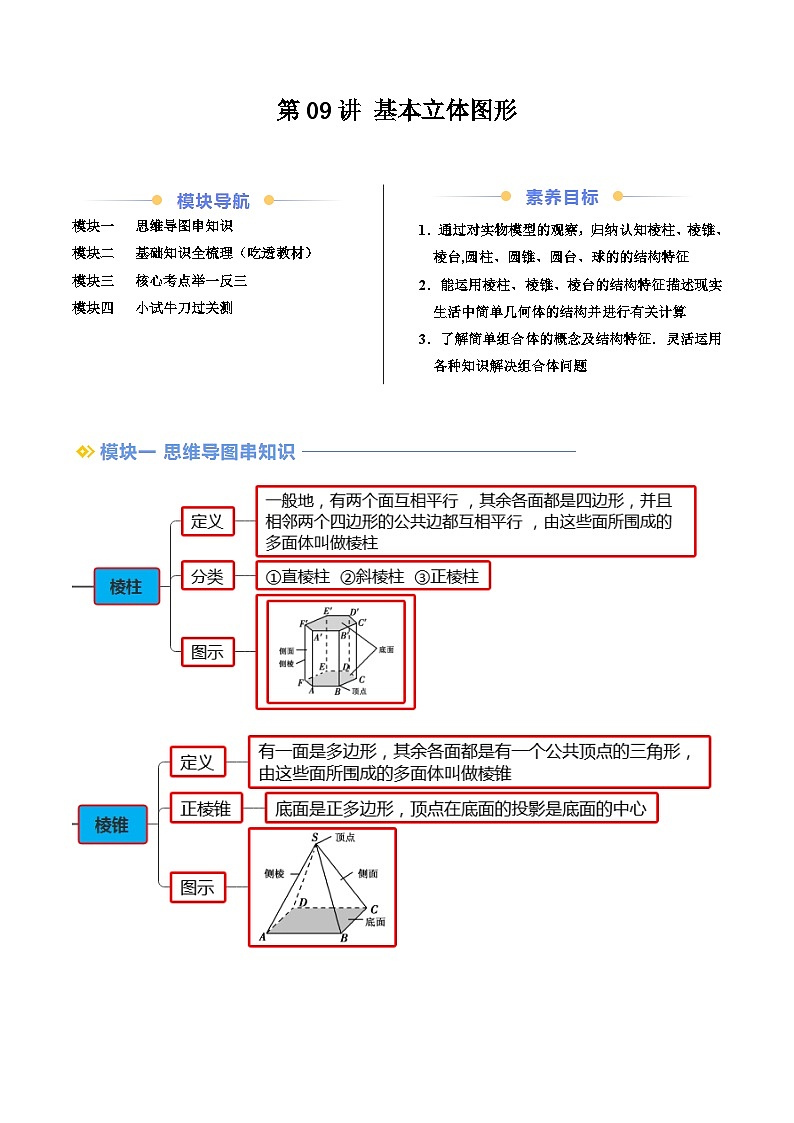
定义：一般地，有两个面互相平行 ，其余各面都是四边形，并且相邻两个四边形的公共边都互相平行 ，由这些面所围成的多面体叫做棱柱
底面(底)：两个互相平行的面
侧面：其余各面
侧棱：相邻侧面的公共边
顶点：侧面与底面的公共顶点
（2）棱柱的图形
（3）棱柱的分类及表示
①按棱柱底面边数分类:
②按棱柱侧棱与底面位置关系分类:
③直棱柱：侧棱垂直于底面的棱柱
斜棱柱：侧棱不垂直于底面的棱柱
正棱柱：底面是正多边形的直棱柱
平行六面体：底面是平行四边形的四棱柱
表示法：用各顶点字母表示棱柱，如图棱柱
知识点3 棱锥
（1）棱锥的定义
定义：有一面是多边形，其余各面都是有一个公共顶点的三角形，由这些面所围成的多面体叫做棱锥
底面：多边形面
侧面：有公共顶点的各三角形面
侧棱：相邻侧面的公共边
顶点：各侧面的公共顶点
（2）棱锥的图形
（3）棱锥的分类及表示
按照棱锥的底面多边形的边数，棱锥可分为： 三棱锥、四棱锥、五棱锥……
特别地，三棱锥又叫四面体，底面是正多边形，且顶点与底面中心的连线垂直于底面的棱锥叫做正棱锥
表示法：棱锥也用顶点和底面各顶点字母表示，如图棱锥
知识点4 棱台
（1）棱台的定义
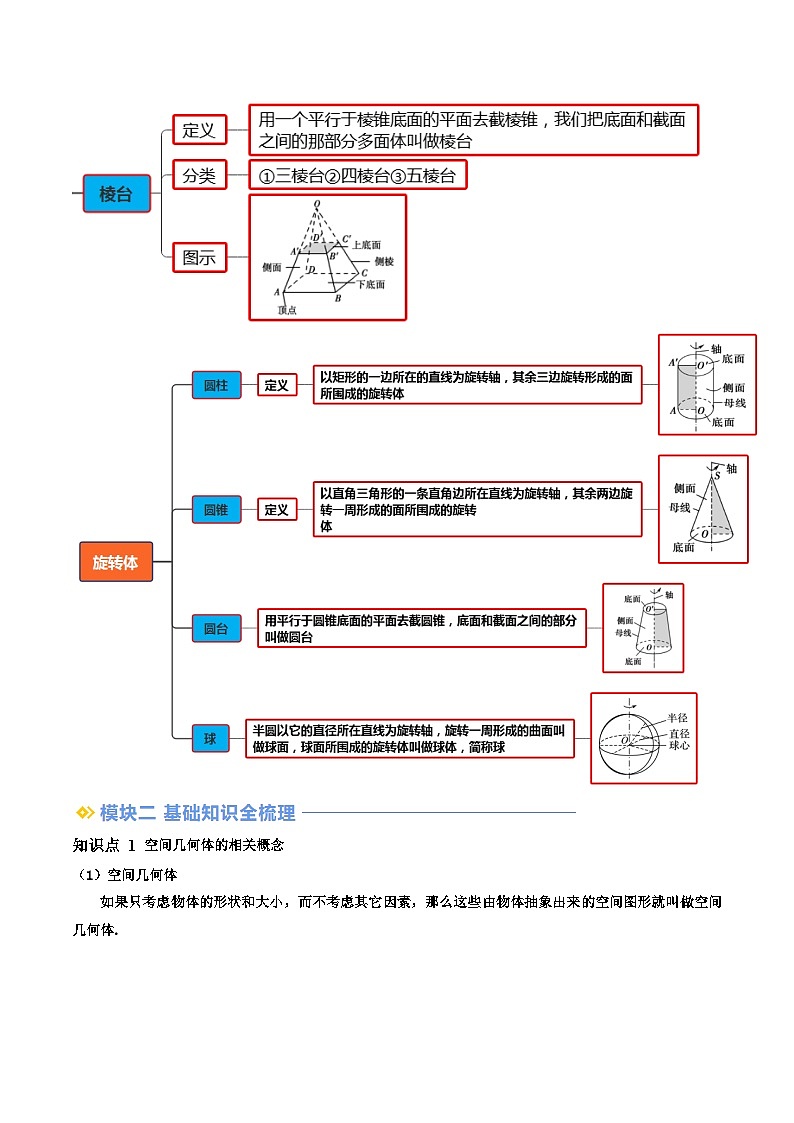
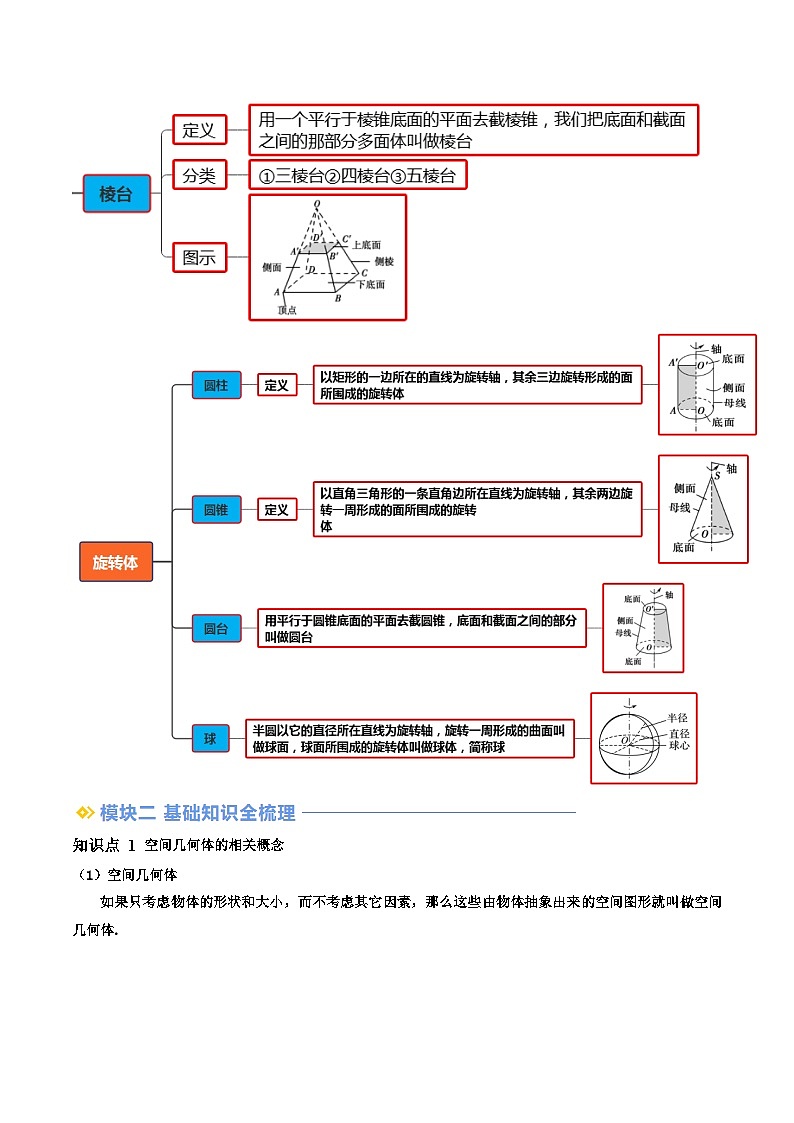
定义：用一个平行于棱锥底面的平面去截棱锥，我们把底面和截面之间的那部分多面体叫做棱台
上底面：原棱锥的截面
下底面：原棱锥的底面
侧面：除上下底面以外的面
侧棱：相邻侧面的公共边
顶点：侧面与上(下)底面的公共顶点
（2）棱台的图形
（3）棱台的分类及表示
由三棱锥、四棱锥、五棱锥……截得的棱台分别叫做三棱台、四棱台、五棱台……
用各顶点字母表示棱柱，如棱台
知识点5 圆柱
（1）圆柱的定义
以矩形的一边所在的直线为旋转轴，其余三边旋转形成的面所围成的旋转体
圆柱的轴：旋转轴
圆柱的底面：垂直于轴的边旋转而成的圆面
圆柱的侧面：平行于轴的边旋转而成的曲面
圆柱侧面的母线：无论旋转到什么位置，平行于轴的边
（2）圆柱的图形
（3）圆柱的表示
圆柱用表示它的轴的字母表示，如图，圆柱
知识点6 圆锥
（1）圆锥的定义
以直角三角形的一条直角边所在直线为旋转轴，其余两边旋转一周形成的面所围成的旋转体
轴：旋转轴叫做圆锥的轴
底面：垂直于轴的边旋转而成的圆面
侧面：直角三角形的斜边旋转而成的曲面
母线：无论旋转到什么位置，不垂直于轴的边
锥体：棱锥和圆锥统称为锥体
（2）圆锥的图形
（3）圆锥的表示
用表示它的轴的字母表示，如图，圆锥
知识点7 圆台
（1）圆台的定义
用平行于圆锥底面的平面去截圆锥，底面和截面之间的部分叫做圆台
轴：圆锥的轴
底面：圆锥的底面和截面
侧面：圆锥的侧面在底面与截面之间的部分
母线：圆锥的母线在底面与截面之间的部分
台体：棱台和圆台统称为台体
（2）圆台的图形
（3）圆台的表示
用表示它的轴的字母表示，如图，圆台
知识点8 球的结构特征
（1）定义：半圆以它的直径所在直线为旋转轴，旋转一周形成的曲面叫做球面，球面所围成的旋转体叫做
球体，简称球
（2）相关概念：
球心：半圆的圆心
半径：连接球心和球面上任意一点的线段
直径：连接球面上两点并经过球心的线段
考点一：棱柱的结构特征
例1．（24-25高二·上海·随堂练习）下列说法中正确的是（ ）．
A．棱柱的面中，至少有两个面互相平行
B．棱柱中两个互相平行的平面一定是棱柱的底面
C．棱柱中一条侧棱就是棱柱的高
D．棱柱的侧面一定是平行四边形，但它的底面一定不是平行四边形
【变式1-1】（2024高一下·全国·专题练习）下列命题中正确的是（ ）
A．有两个面互相平行，其余各面都是四边形的几何体叫棱柱
B．棱柱中互相平行的两个面叫棱柱的底面
C．棱柱的侧面都是平行四边形，而底面不是平行四边形
D．棱柱的侧棱都相等，侧面是平行四边形
【变式1-2】（2024高一下·全国·专题练习）下列说法正确的是（ ）
A．棱柱中相邻两个面的公共边叫做侧棱
B．棱柱中至少有两个面的形状完全相同
C．棱柱中两个互相平行的面一定是棱柱的底面
D．有两个面互相平行，其余各面都是平行四边形的几何体一定是棱柱
【变式1-3】（多选）（23-24高一下·山东青岛·期中）下列有关平行六面体的命题正确的是（ ）
A．平行六面体中相对的两个面是全等的平行四边形
B．平行六面体的八个顶点在同一球面上
C．平行六面体的四个侧面不可能都是矩形
D．平行六面体任何两个相对的面都可以作为它的底面
考点二：棱锥，棱台的结构特征
例2.（多选）（23-24高二上·海南海口·开学考试）棱台具备的特点有（ ）
A．两底面相似B．侧面都是梯形
C．侧棱都相等D．侧棱延长后都交于一点
【变式2-1】（2024高一下·全国·专题练习）下列说法中正确的是（ ）
A．各侧棱都相等的棱锥为正棱锥
B．各侧面都是面积相等的等腰三角形的棱锥为正棱锥
C．各侧面都是全等的等腰三角形的棱锥为正棱锥
D．底面是正多边形且各侧面是全等三角形的棱锥为正棱锥
【变式2-2】（23-24高三上·江苏南通·期末）从正方体的八个顶点中选择四个顶点构成空间四面体，则该四面体不可能（ ）
A．每个面都是等边三角形
B．每个面都是直角三角形
C．有一个面是等边三角形，另外三个面都是直角三角形
D．有两个面是等边三角形，另外两个面是直角三角形
【变式2-3】（23-24高一下·安徽·阶段练习）下列叙述正确的是（ ）
A．用一个平面去截棱锥，棱锥底面和截面之间的部分是棱台
B．两个面平行且相似，其余各面都是梯形的多面体是棱台
C．有两个面互相平行，其余四个面都是等腰梯形的六面体是棱台
D．棱台的侧棱延长后必交于一点
考点三：圆柱的结构特征
例3.（23-24高一下·浙江台州）将正方形绕其一条边所在的直线旋转一周，所得的几何体是（ ）
A．圆柱B．圆台C．圆锥D．棱柱
【变式3-1】（23-24高二·全国·课后作业）一个长方形的两边长分别为和，将其绕一边进行旋转，能得到不同的圆柱的种数为（ ）
A．B．C．D．
【变式3-2】（23-24高一下·黑龙江鸡西）圆柱侧面的母线有 条.
【变式3-3】（2024高一·全国·专题练习）圆柱的轴截面有 个，它们 (填“全等”或“相似”)，圆柱的母线有 条，它们与圆柱的高 ．
考点四：棱柱展开图中最短距离问题
例4（23-24高一下·陕西西安·阶段练习）如图，棱长为2的正方体中，点在线段上运动，则的最小值为 .
【变式4-1】（23-24高一下·江苏苏州·阶段练习）如图，已知正三棱柱的底面边长为，高为，一质点自点出发，沿着三棱柱的侧面绕行一周到达点的最短路线的长为 .

【变式4-2】（23-24高三下·贵州·阶段练习）已知棱长为的正方体中，为棱上一动点，则的最小值为 .
【变式4-3】（2024·江西九江·一模）如图，在正三棱柱中，，为的中点，为线段上的点.则的最小值为

考点五：棱锥展开图中最短距离问题
例5.（2024高三·全国·专题练习）如图，是正三棱锥且侧棱长为，两侧棱的夹角为分别是上的动点，则三角形的周长的最小值为（ ）

A．B．C．D．
【变式5-1】（23-24高一下·河北石家庄·期中）如图，在正四棱锥中，，．从A拉一条细绳绕过侧棱PB到达C点，则细绳的最短长度为 ．
【变式5-2】（23-24高一下·山东滨州·阶段练习）如图，正三棱锥中，，侧棱长为4，过点C的平面与侧棱AB，AD相交于，则的周长的最小值为 ．
考点六：圆柱展开图中最短距离问题
例6.（24-25高二上·贵州遵义·阶段练习）如图所示，有一个圆柱，在圆柱下底面的点A处有一只蚂蚁，它要爬行到上底面的点B处.当圆柱的高等于8cm，底面半径为3cm时，蚂蚁沿圆柱表面爬行的最短路程是（ ）
A．12 cmB． cm
C．18 cmD．cm
【变式6-1】（23-24高一下·河南南阳·期末）如图，某圆柱的一个轴截面是边长为2的正方形ABCD，点E在下底面圆周上，且，点F在母线AB上，点G是线段AC的靠近点A的四等分点，则的最小值为（ ）

A．B．3C．4D．
【变式6-2】（24-25高二上·上海·期中）如图，一圆柱体的底面周长为，高为，是底面的直径.一只昆虫从点出发，沿着圆柱的侧面爬行到点，则昆虫爬行的最短距离是 .
考点七：圆锥展开图中最短距离问题
例7.（24-25高三上·广东·开学考试）圆锥顶点，底面半径为1，母线的中点为，一只蚂蚁从底面圆周上的点绕圆锥侧面一周到达的最短路线中，其中下坡路的长是（ ）
A．0B．C．D．
【变式7-1】（2024高三·全国·专题练习）圆锥的底面半径为，母线长，一只蚂蚁自底面圆周上一点沿圆锥表面爬到过母线的轴截面上另一条母线的中点，问这只蚂蚁爬行的最短距离为 .
【变式7-2】（2024高一下·浙江·专题练习）如图，圆锥的母线长是3，底面半径是1，是底面圆周上一点，从点出发绕侧面一周，再回到点的最短的路线长是 .
考点八：截面问题
例8.（2024高三·全国·专题练习）如图，正方体的棱长为分别为棱的中点.请在正方体的表面完整作出过点的截面，并写出作图过程；（不用证明）
【变式8-1】（24-25高二上·广西柳州·期中）如图，正方体的棱长为2，E，F分别为的中点，则平面AEF截正方体所得的截面面积为 .
【变式8-2】（23-24高二下·上海）已知正四面体棱长为2，所有与它四个顶点距离相等的平面截这个四面体所得的截面之和为 ．
【变式8-3】（223-24高二下·河北石家庄）若圆柱的底面半径为2，轴截面的对角线长为5，则这个圆柱侧面展开图的对角线长为 .
【变式8-4】（24-25高二上·上海·期中）已知圆锥底面半径为，高为1，则过圆锥的母线的截面面积的最大值为 ．
考点九：球的有关计算
例9.（23-24高二·上海·课堂例题）若平面截球O所得圆的半径为1，球的表面积是，则球心O到平面的距离为 ．
【变式9-1】（23-24高二上·河北唐山·开学考试）已知圆柱的高为2，它的两个底面的圆周在直径为4的同一个球的球面上，则该圆柱的体积为（ ）
A．B．C．D．
【变式9-2】（2024·山西·三模）某公司在庆典活动中，设计了一款纪念品如图所示，其底座是顶部有凹槽的圆台，上面放置一个水晶玻璃球，圆台上底圆周的所有点都在凹槽面上四槽面上的所有点都在球面上圆台的上、下底面半径分别为2cm，4cm，母线长为cm，球的顶端到底座下底面的距离为8cm，则水晶球的半径为（ ）
A．cmB．cmC．cmD．cm
【变式9-3】（24-25高二上·上海·期中）若球的半径为5，圆为该球的一个小圆且面积为，则线段的长度是 .
一、单选题
1．（2024高二上·黑龙江佳木斯·学业考试）一个直角三角形绕它的一条直角边所在直线旋转形成的曲面所围成的几何体是（ ）
A．球体B．圆柱C．圆台D．圆锥
2．（2024高三·全国·专题练习）下面关于空间几何体叙述正确的是（ ）
A．底面是正多边形的棱锥是正棱锥
B．有两个面互相平行，其余各面都是梯形的多面体是棱台
C．正四棱柱都是长方体
D．直角三角形以其直角边所在直线为轴旋转一周形成的几何体是圆柱
3．（24-25高二上·北京·阶段练习）下列四个命题中正确的是（ ）
A．正三棱锥的每个面都是正三角形
B．所有棱长都相等的四棱柱是正方体
C．以矩形的一边所在直线为旋转轴，其余三边旋转一周形成的面所围成的旋转体叫做圆柱
D．以直角三角形的一边所在直线为旋转轴，其余两边旋转一周形成的面所围成的旋转体叫做圆锥
4．（24-25高一下·全国·课前预习）如图所示的组合体，则由下列所示的哪个三角形绕直线l旋转一周可以得到（ ）
A．B．C．D．
5．（23-24高一下·北京大兴·期中）在三棱台中，截去三棱锥，则剩余部分是（ ）
A．三棱锥B．三棱台
C．四棱锥D．组合体
6．（24-25高一下·全国·课后作业）图①②中的图形折叠后的图形分别是（ ）

A．圆锥、棱柱B．圆锥、棱锥C．球、棱锥D．圆锥、圆柱
7．（24-25高二上·安徽合肥·期中）如图，在长方体中，，若点在平面上运动，则的最小值为（ ）
A．B．C．D．
8．（23-24高一下·吉林·期中）如图，在正四棱锥中，是棱上的动点，一只蚂蚁从A点出发，经过E点，爬到C点，则这只蚂蚁爬行的路程的最小值是（ ）
A．B．C．D．
二、多选题
9．（2025高三·全国·专题练习）（多选）下列说法正确的是（ ）
A．以直角三角形的一条边所在的直线为轴，其余两边旋转形成的曲面围成的几何体是圆锥
B．以等腰三角形底边上的中线所在的直线为轴，将三角形旋转形成的曲面围成的几何体是圆锥
C．经过圆锥任意两条母线的截面是等腰三角形
D．圆锥侧面的母线长有可能大于圆锥底面圆的直径
10．（23-24高一下·河北邢台·期中）用一个平面去截一个几何体，截面是四边形，则这个几何体可能是（ ）
A．圆锥B．圆柱C．三棱柱D．三棱锥
三、填空题
11．（24-25高二上·上海·阶段练习）如图，棱长为1的正方体中，为线段的中点，、分别为线段和棱上任意一点，则的最小值为 .
12．（2024高三·全国·专题练习）正方体的棱长为3，E，F是棱，上的中点，平面截正方体所得截面的周长为
13．（24-25高三上·河北承德·期中）将扇形纸壳OCD剪掉扇形OAB后得到扇环，，，如图1，用扇环制成一个圆台的侧面，如图2，则该圆台的高为 .
14．（24-25高二上·上海浦东新·期中）如图，正方体的棱长是，是上的动点，、是上、下两底面上的动点，是中点，，则的最小值是 .
15．（24-25高二上·天津武清·期中）如图，正方体的棱长为2，若，分别是线段，的中点，则线段的长为 ．
模块一 思维导图串知识
模块二 基础知识全梳理（吃透教材）
模块三 核心考点举一反三
模块四 小试牛刀过关测
1．通过对实物模型的观察，归纳认知棱柱、棱锥、棱台,圆柱、圆锥、圆台、球的的结构特征
2．能运用棱柱、棱锥、棱台的结构特征描述现实生活中简单几何体的结构并进行有关计算
3．了解简单组合体的概念及结构特征．灵活运用各种知识解决组合体问题