第04讲 函数的极值与导数-【寒假提升课】2025年高二数学寒假提升试题（人教A版2019）

这是一份第04讲 函数的极值与导数-【寒假提升课】2025年高二数学寒假提升试题（人教A版2019），文件包含第04讲函数的极值与导数思维导图+2知识点+四大考点+过关检测原卷版docx、第04讲函数的极值与导数思维导图+2知识点+四大考点+过关检测解析版docx等2份试卷配套教学资源，其中试卷共37页， 欢迎下载使用。

一、函数的极值
（1）函数的极小值
如果对附近的所有点都有，而且在点附近的左侧，右侧，则称是函数的一个极小值，记作．
（2）函数的极大值
函数在点附近有定义，如果对附近的所有点都有，而且在点附近的左侧，右侧，则称是函数的一个极大值，记作．
（3）极小值点、极大值点统称为极值点，极小值和极大值统称为极值．
二、求函数极值的步骤
①先确定函数的定义域；
②求导数；
③求方程的解；
④检验在方程的根的左右两侧的符号，如果在根的左侧附近为正，在右侧附近为负，那么函数在这个根处取得极大值；如果在根的左侧附近为负，在右侧附近为正，那么函数在这个根处取得极小值．
【注意】
（1）可导函数的极值点．必须是导数为0的点，但导数为0的点不一定是极值点．
即“点x0是可导函数f(x)的极值点”是“f′(x0)＝0”的充分不必要条件．
不可导的点可能是极值点也可能不是极值点．
例如：①导数为0的点是极值点：y＝x2，y′|x＝0＝0，x＝0是极值点．
②导数为0的点不是极值点：y＝x3，y′|x＝0＝0，x＝0不是极值点．
③不可导的点是极值点：y＝|sinx|，x＝0不可导，但x＝0是极值点．
（2）函数的极值只是一个局部性的概念，是仅对某一点及左、右两侧区域而言的．在函数的整个定义区间内可能有多个极大值或极小值，且极大值不一定比极小值大，如图，
点x1、x3是极大值点，x2、x4是极小值点，且在点x1处的极大值小于在点上x4处的极小值．
（3）极值点是自变量的值，极值指的是函数值．
（4）函数的极值点一定出现在区间的内部，区间的端点不能成为极值点．
（5）若f(x)在(a，b)内有极值，那么f(x)在(a，b)内绝对不会是单调函数，即在区间上的单调函数没有极值．
【考点一：函数图像与极值（点）的联系】
一、单选题
1．（23-24高二下·重庆九龙坡·期中）已知函数的导函数f'x的大致图象如图所示，则下列结论一定正确的是（ ）
A．B．
C．D．
2．（23-24高二下·浙江·期中）函数的图象如图所示，则下列结论成立的是（ ）
A．B．
C．D．
二、多选题
3．（23-24高二下·新疆乌鲁木齐·期中）已知函数的导函数的图象如图所示，则下列选项中正确的是（ ）
A．函数在处取得极大值B．函数在处取得极值
C．在区间-2,3上单调递减D．的图象在处的切线斜率小于零
4．（23-24高二下·河北唐山·期中）观察图象，下列结论错误的有（ ）
A．若图中为图象，则在处取极小值
B．若图中为图象，则两个极值点
C．若图中为图象，则在0,2上单调递增
D．若图中为图象，则的解集为
【考点二：不含参数的函数求极值（点）】
一、单选题
1．（23-24高二下·江西吉安·期末）函数满足，则的极大值点为（ ）
A．4B．8C．10D．12
2．（22-23高二下·广西柳州·阶段练习）若函数的极值点为（ ）
A．B．C．D．
3．（24-25高二上·全国·课后作业）函数的极大值与极小值之和为（ ）
A．B．C．D．
4．（23-24高二下·江西新余·期末）若函数，则的极大值点的个数为（ ）
A．1B．2C．3D．4
二、填空题
5．（23-24高二下·广东佛山·阶段练习）已知函数，则的极小值点为 .
6．（23-24高三上·江苏·阶段练习）函数的极大值是 ．
【考点三：含参数的函数求极值（点）】
一、解答题
1．（23-24高二下·四川内江·期中）已知函数，
(1)讨论函数的极值点情况；
(2)若，证明.
2．（23-24高二下·云南昆明·期末）已知函数．
(1)当时，求过点的切线方程；
(2)若有极值且恒成立，求的取值范围．
3．（23-24高二下·安徽亳州·期末）已知函数，其中为自然对数的底数．
(1)求的极值；
(2)若有两个零点，求的取值范围．
4．（2024·山东济南·一模）已知函数.
(1)当时，求的单调区间；
(2)讨论极值点的个数.
5．（22-23高二下·陕西咸阳·阶段练习）已知函数．
(1)当时，求曲线在点处的切线方程；
(2)讨论函数的极值点个数．
6．（24-25高二上·全国·课后作业）已知函数．
(1)当时，求函数的单调区间；
(2)若均不为零，讨论函数的极值．
【考点四：已知函数的极值（点）求参数】
一、单选题
1．（2024·辽宁·模拟预测）已知函数在处有极大值，则（ ）
A．1B．2C．3D．4
2．（23-24高二下·山东临沂·期中）已知函数，当时，有极大值．则（ ）
A．2B．1C．0D．
3．（23-24高二上·江苏南通·阶段练习）已知函数在处取得极小值10，则的值为（ ）
A．2或B．或C．D．
二、填空题
4．（24-25高二下·全国·课后作业）写出“使得函数在区间上有唯一极值点”的整数的一个值 ．
5．（23-24高二下·福建龙岩·期中）函数既有极大值，又有极小值，则整数a的最大值为 ．
6．（23-24高二下·福建龙岩·阶段练习）若函数在区间无零点但有2个极值点，则实数的取值范围是 ．
一、单选题
1．（23-24高二下·甘肃天水·阶段练习）已知函数的导函数f'x的图象如图，则下列叙述正确的是（ ）
A．函数在上单调递减
B．函数在处取得极小值
C．函数在处取得极值
D．函数只有一个极值点
2．（23-24高二下·山东淄博·阶段练习）若函数在内无极值，则实数的取值范围是（ ）
A．B．
C．D．
3．（23-24高二下·河南周口·阶段练习）已知函数的极值为，则实数（ ）
A．B．C．D．
4．（23-24高二下·北京大兴·期中）已知函数有两个极值点，则实数的取值范围是（ ）
A．B．
C．D．
二、多选题
5．（23-24高三上·广东江门·开学考试）已知函数，且满足，则（ ）
A．函数在处有极大值
B．函数在区间上是增函数
C．函数在有极大值
D．函数在区间和上是增函数
6．（23-24高二下·四川凉山·期中）若函数有两个极值，则（ ）
A．B．
C．D．
7．（23-24高二下·广东·阶段练习）如图，已知直线与曲线y=fx相切于两点，函数，则关于函数有关极值的结论错误的是（ ）
A．有极小值没有极大值B．有极大值没有极小值
C．至少有两个极小值和一个极大值D．只有一个极小值和两个极大值
8．（23-24高二下·四川凉山·期中）已知函数，则下列说法正确的有（ ）
A．若是上的增函数，则
B．当时，函数有两个极值
C．当时，函数有两零点
D．当时，在点处的切线与只有唯一个公共点
三、填空题
9．（23-24高二下·河北石家庄·期末）函数在处有极值10，则实数 ．
10．（23-24高二下·重庆·阶段练习）已知函数有极值，则a的取值范围是 .
四、解答题
11．（23-24高二下·甘肃兰州·期中）已知曲线：.
(1)求在点处的切线方程；
(2)求的极值.
12．（24-25高二上·全国·课后作业）已知函数．
(1)当时，求函数的极值；
(2)讨论的单调性．
13．（23-24高二下·北京朝阳·期中）已知函数
(1)求曲线在处的切线方程；
(2)设函数，求的单调区间；
(3)指出极值点的个数，并说明理由.
14．（23-24高二下·辽宁沈阳·阶段练习）已知函数．
(1)在定义域内单调递减，求的范围；
(2)讨论函数在定义域内的极值点的个数；
(3)若函数在处取得极值，恒成立，求实数的取值范围．
15．（23-24高二下·河南洛阳·期中）给定函数.
(1)判断函数的单调性，并求出函数的极值;
(2)证明:当时，.
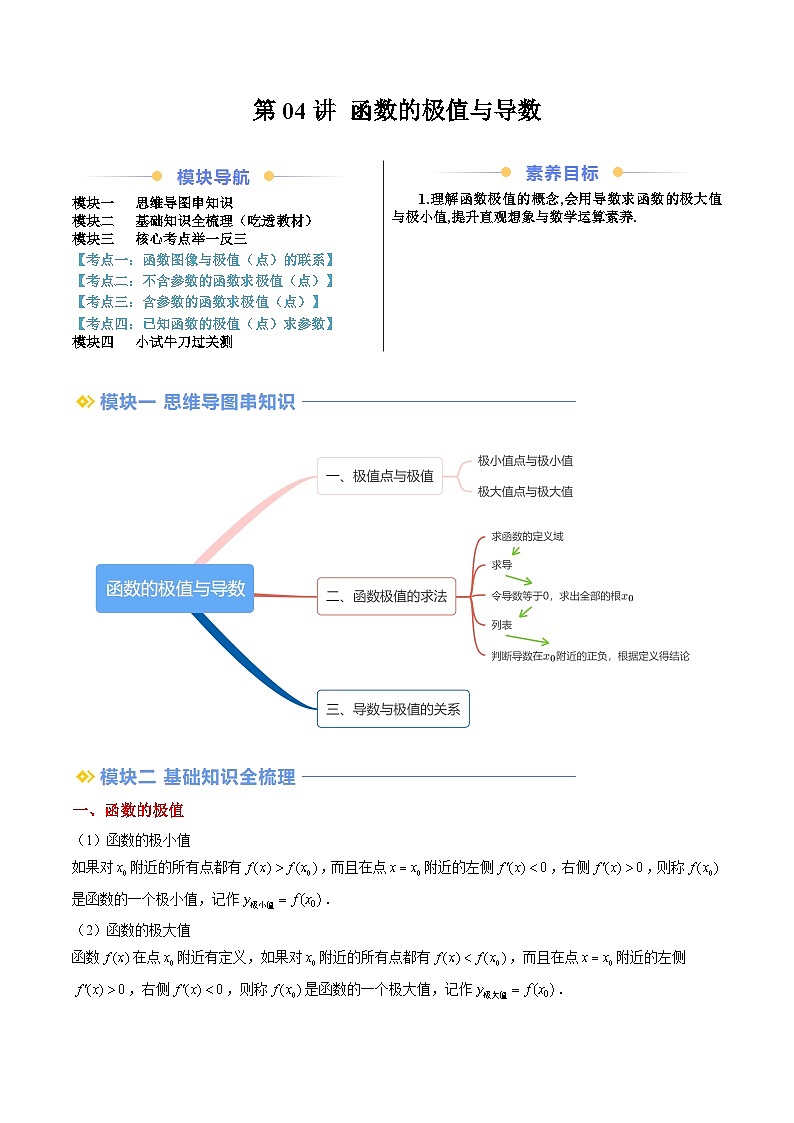
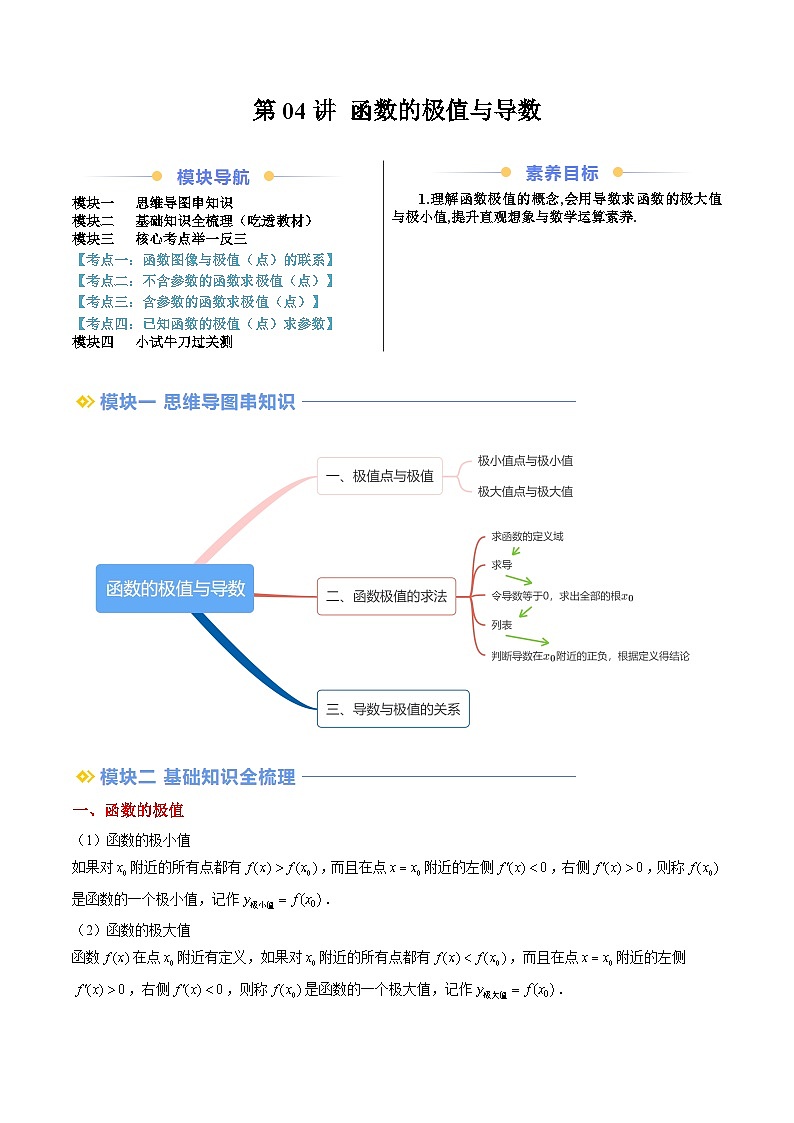
模块一 思维导图串知识
模块二 基础知识全梳理（吃透教材）
模块三 核心考点举一反三
【考点一：函数图像与极值（点）的联系】
【考点二：不含参数的函数求极值（点）】
【考点三：含参数的函数求极值（点）】
【考点四：已知函数的极值（点）求参数】
模块四 小试牛刀过关测
1.理解函数极值的概念,会用导数求函数的极大值与极小值,提升直观想象与数学运算素养.