初中数学新湘教版七年级上册第2章 代数式复习教学课件2024秋

这是一份初中数学新湘教版七年级上册第2章 代数式复习教学课件2024秋，共28页。
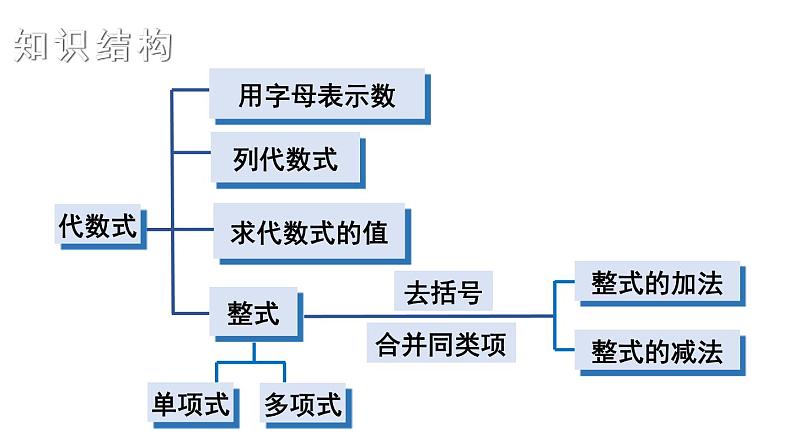
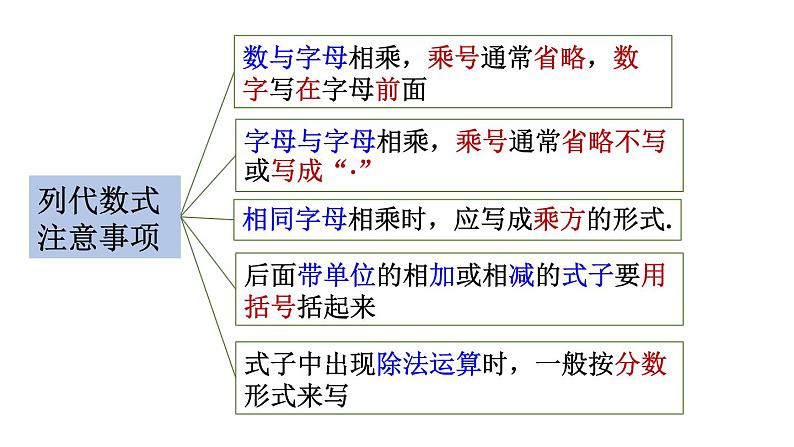
湘教版·七年级上册章末复习知识结构用字母表示数列代数式整式整式的加法代数式求代数式的值单项式多项式整式的减法思考回顾1.什么叫作代数式？列代数式时，一般怎样规范书写？数与表示数的字母用运算符号连接而成的式子叫作代数式.单独一个字母或一个数也是代数式.列代数式注意事项1用代数式填空:(1) 正方形的边长为a，那么它的周长是_______，面积是 _______;(2）某地区去年的人均收入为b万元，今后一段时期每年 将以9%的增长率增加，则经过三年增长，该地区人 均收入为___________万元．4aa2(1+9%)3b2.列代数式：(1) x 的立方减去 y 的4倍；(2) a 的相反数与 b(b不为0)的倒数的和；(3) a 减去 b 的差的平方，再加上a与b的和的平方.x2-4y (a-b)2+(a+b)22. 举例说明如何求代数式的值？代数式372.6+4.07b代入数值时，应该把省略的乘号还原.代入负数时，根据实际情况添上括号.乘方运算代入分数时，也必须添上括号.计算时必须按照代数式指定的运算顺序进行计算.注意事项：  3.什么叫作单项式、多项式？单独一个数或字母是单项式吗？单项式的次数、多项式的次数分别是如何确定的？(1)单项式: ①定义:____________________________的代数式叫做单项式. ②系数:单项式中的_______叫做这个单项式的系数. ③次数:单项式中，所有字母的指数______叫做这个 单项式的次数. ④单独的一个数或字母是单项式.的和数字由数与字母及其幂的乘积组成(2)多项式: ①定义:几个单项式的__________叫做多项式. ②多项式的项:多项式里，每个__________叫做多项式 的项(包含前面符号). 常数项:不含______的项叫做常数项（包含前面符号)； ③多项式的次数:多项式中，次数最高的项的________， 叫作这个多项式的次数.和单项式字母次数(1) 单项式23x2y的系数是 _____，次数是_____.(2) 多项式x3y2-2x2y+5xy2-6的次数是_____，项有____________________，常数项是______，是____次____项式，并按字母____的____幂排序.835x3y2,-2x2y,5xy2, -6 -6 五四降x4.什么叫作同类项？怎样合并同类项？ 把所含字母相同并且相同字母的指数也相同的单项式称为同类项. 一般地，在多项式中，要把同类项的系数相加合并成一项，这叫作合并同类项.同类项的特征：两相同所含______相同. 相同字母的______分别相同.两无关两者缺一不可与__________无关. 与__________无关.字母系数大小字母顺序所有的常数项都是同类项指数“合并同类项”的方法:一找，找出多项式中的同类项，不同类的同类项用 不同的标记标出;二移，利用加法的交换律，将不同类的同类项集 中到一起;三合，将同一括号内的同类项相加即可.系数相加，字母和字母的指数不变.1、下列各组是不是同类项：（1）4abc 与 4ab （2）–5 m2 n3 与 2n3 m2（3）–0.3 x2 y 与 y x2不是是是2、合并下列同类项：（1）3xy – 4 xy – xy = （ ） （2）– a – a – 2a=（ ） （3）0.8ab3 – a3 b+0.2ab3 =（ ）–2xy–4aab3–a3b5.举例说明如何进行整式的加减运算.去括号法则: 括号前是“+”，可以直接去掉括号，原括号里各项符号都不变; 括号前是“- ”，去掉括号和它前面的“-”时，原括号里各项符号均要改变.思考：括号前面有系数怎么办？-7(a+b)2(x+y)分析：1.用括号前面的数乘以括号内的每一项； 2.再根据去括号法则去括号.-7(a+b)= -(7a+7b)=-7a-7b2(x+y)=2x+2y计算2x2-3x+1与-3x2+ 5x-7的和.分析:把多项式看作一个整体，并用括号括起来.(见多必括)(2x2-3x+1) +(-3x2+ 5x-7)解：= 2x2-3x+1-3x2+ 5x-7= (2-3)x2+(-3+5)x+(1-7)= -x2+2 x -6 .······去括号······合并同类项（2）5a2 －[a2+(5 a2 －2a) －2(a2 －3a)]（1） 3(xy2－x2y) －2(xy+xy2)+3x2y；1.计算= 3xy2－3x2y －2xy － 2xy2+3x2y= xy2 － 2xy= 5a2 －a2 － 5a2 +2a+2a2 －6a= a2 － 4a课堂练习1.(1) 在下列单项式中，与2x2y是同类项的是( )A.x3y2 B. 3xy2 C. -x2y D. 2xy (2) 若 2x3yn 与-xmy2是同类项，则 m+n=______.C5(3) 计算:a+(5a-3b)-(a-2b)解：a+(5a-3b)-(a-2b)= a+5a-3b-a+2b= 5a-b其中 x = – 1 ，y = 2 .2.解 6xy – [3x2–2（x2–2xy）+1] = 6xy–3x2+2x2–4xy–1 = –x2+ 2xy –1当 x = – 1 ，y = 2时，原式= –（–1）2+2×（–1 ）×2–1= –6解 A+5B =（x+2y）+5（3x–5y）= x+2y+15x–25y= 16x–23y4.(1)若a+b=7 ，ab=10，求(5ab+4a+7b)+(6a-3ab)-(4ab-3b)的值；(2)若a2＋2ab=-2，ab-b2=-4，求2a2+5ab-b2的值.解：(1) (5ab+4a+7b)+(6a-3ab)-(4ab-3b)= 5ab+4a+7b+6a-3ab-4ab+3b= -2ab+10a+10b= -2ab+10(a+b)= -2×10+10×7= 504.(1)若a+b=7 ，ab=10，求(5ab+4a+7b)+(6a-3ab)-(4ab-3b)的值；(2)若a2＋2ab=-2，ab-b2=-4，求2a2+5ab-b2的值. (2) 2a2+5ab-b2= 2(a2+2ab) + (ab-b2)= 2×(-2) + (-4)= -4-4= -8课后作业1.从课后习题中选取；2.完成练习册本课时的习题.