江苏省无锡市新城中学2024-2025学年七（上）数学第17周阶段性训练模拟练习【含答案】

这是一份江苏省无锡市新城中学2024-2025学年七（上）数学第17周阶段性训练模拟练习【含答案】，共20页。试卷主要包含了下列说法等内容，欢迎下载使用。
1．如图，点D是线段AC上一点，点C是线段AB的中点，则下列等式不成立的是（ ）
A．AD+BD＝ABB．BD﹣CD＝CBC．AB＝2ACD．
2．下列说法：①两点之间线段最短；②同角的余角相等；③相等的角是对顶角；④直线外一点与直线上各点连接的所有线段中，垂线段最短．其中正确的有（ ）
A．1个B．2个C．3个D．4个
3．“铃铃铃”上课铃声响了，小明一看时间是下午2点30分，如果一节课是45分钟，那么下课时刻分针和时针的夹角大小是（ ）
A．15°B．7.5°C．5°D．0°
4．在如图所示的三阶幻方中，填写了一些数、式子和汉字（其中每个式子或汉字都表示一个数），若每一横行，每一竖列，以及每条对角线上的3个数之和都相等，则“坚持不懈”这四个字表示的数之和为（ ）
A．18B．19C．21D．22
5．如图，点B，O，D在同一直线上，∠AOC＝90°，若∠1＝23°，则∠2的度数为（ ）
A．113°B．107°C．67°D．157°
6．我国古代数学著作《孙子算经》中有如下问题：“今有三人共车，二车空；二人共车，九人步，问人与车各几何？”其意思是：“每车坐3人，空出来2车；每车坐2人，9人没车坐．问人数与车数各为多少？”设车为x辆，根据题意，可列出方程（ ）
A．3x﹣2＝2x+9B．3（x﹣2）＝2x+9
C．+2＝﹣9D．＝
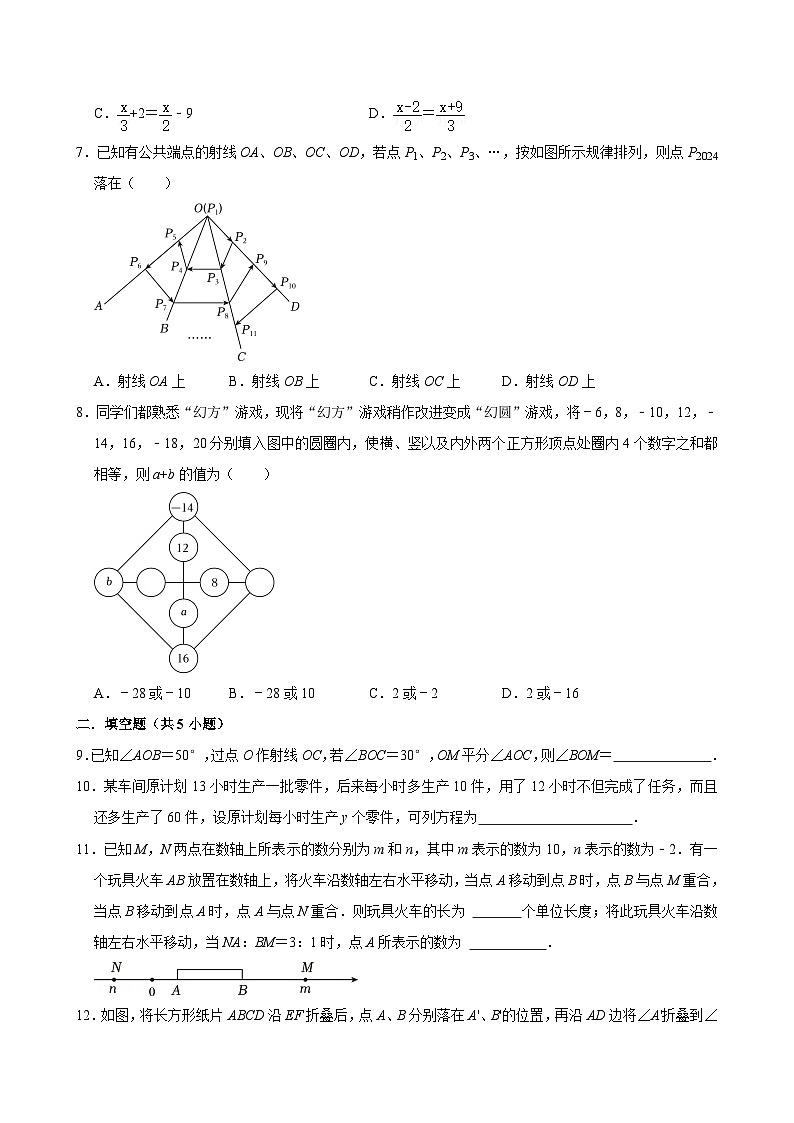
7．已知有公共端点的射线OA、OB、OC、OD，若点P1、P2、P3、…，按如图所示规律排列，则点P2024落在（ ）
A．射线OA上B．射线OB上C．射线OC上D．射线OD上
8．同学们都熟悉“幻方”游戏，现将“幻方”游戏稍作改进变成“幻圆”游戏，将﹣6，8，﹣10，12，﹣14，16，﹣18，20分别填入图中的圆圈内，使横、竖以及内外两个正方形顶点处圈内4个数字之和都相等，则a+b的值为（ ）
A．﹣28或﹣10B．﹣28或10C．2或﹣2D．2或﹣16
二．填空题（共5小题）
9．已知∠AOB＝50°，过点O作射线OC，若∠BOC＝30°，OM平分∠AOC，则∠BOM＝ ．
10．某车间原计划13小时生产一批零件，后来每小时多生产10件，用了12小时不但完成了任务，而且还多生产了60件，设原计划每小时生产y个零件，可列方程为 ．
11．已知M，N两点在数轴上所表示的数分别为m和n，其中m表示的数为10，n表示的数为﹣2．有一个玩具火车AB放置在数轴上，将火车沿数轴左右水平移动，当点A移动到点B时，点B与点M重合，当点B移动到点A时，点A与点N重合．则玩具火车的长为 个单位长度；将此玩具火车沿数轴左右水平移动，当NA：BM＝3：1时，点A所表示的数为 ．
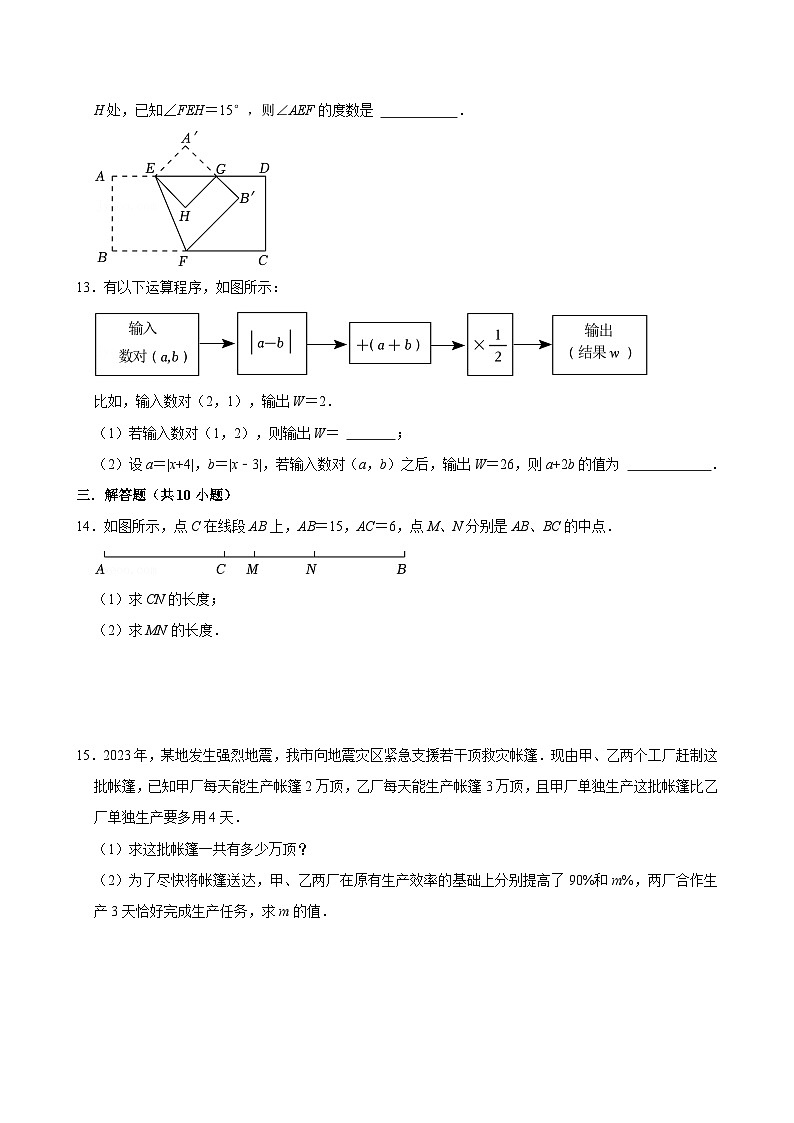
12．如图，将长方形纸片ABCD沿EF折叠后，点A、B分别落在A'、B'的位置，再沿AD边将∠A'折叠到∠H处，已知∠FEH＝15°，则∠AEF的度数是 ．
13．有以下运算程序，如图所示：
比如，输入数对（2，1），输出W＝2．
（1）若输入数对（1，2），则输出W＝ ；
（2）设a＝|x+4|，b＝|x﹣3|，若输入数对（a，b）之后，输出W＝26，则a+2b的值为 ．
三．解答题（共10小题）
14．如图所示，点C在线段AB上，AB＝15，AC＝6，点M、N分别是AB、BC的中点．
（1）求CN的长度；
（2）求MN的长度．
15．2023年，某地发生强烈地震，我市向地震灾区紧急支援若干顶救灾帐篷．现由甲、乙两个工厂赶制这批帐篷，已知甲厂每天能生产帐篷2万顶，乙厂每天能生产帐篷3万顶，且甲厂单独生产这批帐篷比乙厂单独生产要多用4天．
（1）求这批帐篷一共有多少万顶？
（2）为了尽快将帐篷送达，甲、乙两厂在原有生产效率的基础上分别提高了90%和m%，两厂合作生产3天恰好完成生产任务，求m的值．
16．在正方体的八个顶点处各写一个数，使每个顶点处的数等于与这个顶点连接的三条棱上另外三个顶点处的数之和．例如，图（1）中，与点A连接的三条棱上的另外三个顶点处，分别写有1、2、3，那么点A处的数等于1+2+3＝6．请根据这个规则，解答图（2）中的问题：
（1）①若点A、C、E处分别写2、﹣5、0，则点F处的数等于 ；
②若点A、B、C处分别写3、4、7，则点D处的数等于 ．
（2）若点A、C、D处分别写2024、1、23，求E点处的数等于多少？
（3）顶点D、F处的数之间具有什么数量关系？请直接写出答案．
17．定义：从∠α（90°＜α＜180°）的顶点出发，在角的内部作一条射线，若该射线将∠α分得的两个角中有一个角与∠α互为补角，则称该射线为∠α的“好线”．
如图，点O在直线AB上，OC、OD在直线AB上方，且OC⊥OD，射线OE是∠AOD的“好线”．
（1）若∠BOD＝26°，且OE在∠COD内部，则∠COE＝ °；
（2）若OE恰好平分∠AOC，请求出∠BOD的度数；
（3）若OF是∠AOE的平分线，OG是∠BOC的平分线，请画出图形，探究∠EOF与∠DOG的数量关系，并说明理由．
18．已知：如图，∠AOB是直角，∠AOC＝40°，ON是∠AOC的平分线，OM是∠BOC的平分线．
（1）求∠MON的大小；
（2）当锐角∠AOC的大小发生改变时，∠MON的大小是否发生改变？为什么？
19．对联是中华传统文化的瑰宝，对联装裱后，如图所示，上、下空白处分别称为天头和地头，左、右空白处统称为边．一般情况下，天头长与地头长的比是6：4，左、右边的宽相等，均为天头长与地头长的和的．某人要装裱一副对联，对联的长为96cm，宽为26cm．若要求装裱后的长是装裱后的宽的4倍，求边的宽和天头长．（书法作品内容出自王维的诗作《送别》）
20．【问题情境】《制作无盖的长方体纸盒》是苏科版七上的课题学习，某综合实践小组在学习了这一课后，开展了“长方体纸盒的制作”实践活动．
【问题解决】（1）如图所示图形中，是无盖正方体的表面展开图的是 ；（填序号）
（2）综合实践小组利用边长为a（cm）的正方形纸板制作出两种不同方案的长方体盒子（图1为无盖的长方体纸盒，图2为有盖的长方体纸盒）．
①图1方式制作一个无盖的长方体盒子的方法：先在纸板四角剪去四个同样大小边长为b（cm）的小正方形，再沿虚线折合起来．则长方体纸盒的底面周长为 cm；
②图2方式制作一个有盖的长方体纸盒的方法：先在纸板四角剪去两个同样大小边长为b（cm）的小正方形和两个同样大小的小长方形，再沿虚线折合起来．如果a＝30cm，b＝5cm．则该长方体纸盒的体积为 cm3；
【问题进阶】
（3）若一个无盖长方体的长、宽、高分别为6、4、3，它缺一个长为6，宽为4的长方形底面，将它的表面沿某些棱剪开，展开成一个平面图形，则该长方体表面展开图的最大外围周长为 ；通过比较长方体表面展开图取得最大外围周长和最小外围周长的两个图形，你发现了什么规律？你发现的规律是 ．
21．已知A，B，C，D四点在同一直线上，点D在线段AB上．
（1）如图，若线段AB＝24，点C是线段AB的中点，，求线段CD的长度；
（2）若线段AB＝21a，点C是线段AB上一点，且满足 AC＝2BC，AD：BD＝3：4，求线段CD的长度（用含a的式子表示）．
22．某零售店用3800元购进甲、乙两种商品，其中乙商品的件数是甲商品件数的2倍多15件．已知甲商品进价为25元/件，标价为50元/件；乙商品进价为60元/件，标价为100元/件．
（1）求甲乙两种商品各购进多少件？
（2）若甲种商品按标价的9折出售，乙种商品按标价的8.5折出售，且在运输过程中甲商品有10%不慎损坏，不能进行销售，请问这批商品全部售出后，该零售店共获利多少元？
23．如图，∠AOB＝120°，射线OC在平面内．
（1）若射线OC在∠AOB的内部，且OC垂直OB，OM平分∠COA，则∠MOB的度数为 ；
（2）若∠AOC与∠BOC互补，求∠BOC的大小；
（3）若射线OC绕点O从射线OA的反向延长线的位置出发，以每秒1°的速度顺时针旋转；同时射线OA以每秒5°的速度绕点O逆时针旋转，各自旋转180°后停止转动，请直接写出使得射线OA，OB，OC中某一条射线是另两条射线所夹角的角平分线的时间 ．
参考答案与试题解析
一．选择题（共8小题）
1．【解答】解：∵点C是线段AB的中点，
∴AB＝2AC，故选项C符合题意；
∵D是不是线段AC的中点，
∴AD＝CD≠AC，
∴BD﹣AD＝BD﹣CD＝CB，故选项B符合题意；
由图形知AD+BD＝AB，故选项A符合题意；
∵D是不是线段AC的中点，
∴AD≠AC，故选项D不合题意．
故选：D．
2．【解答】解：①两点之间线段最短，正确；
②同角的余角相等，正确；
③相等的角不一定是对顶角，错误；
④直线外一点与直线上各点连接的所有线段中，垂线段最短，正确．
故选：C．
3．【解答】解：由题意得：下课时的时间为：下午3点15分，
∴下课时刻分针和时针的夹角＝15×0.5°＝7.5°，
故选：B．
4．【解答】解：根据题意得，2x+2﹣18＝﹣10+0，
解得x＝3，
∴持表示的数是﹣18+0﹣（﹣10）＝﹣8，
∴每一横行，每一竖列，以及每条对角线上的3个数之和2x+2+0+（﹣8）＝2×3+2﹣8＝0，
∴坚表示的数是0﹣（﹣8）﹣（﹣10）＝0+8+10＝18，不表示的数是0﹣0﹣（x﹣5）＝﹣（3﹣5）＝2，懈表示的数是0﹣（﹣8）﹣（﹣2）＝8+2＝10，
∴“坚持不懈”这四个字表示的数之和为18+（﹣8）+2+10＝22，
故选：D．
5．【解答】解：∵∠AOC＝90°，∠1＝23°，
∴∠BOC＝90°﹣∠1＝67°．
∴∠2＝180°﹣∠BOC＝113°．
故选：A．
6．【解答】解：设车为x辆，
依题意，得：3（x﹣2）＝2x+9．
故选：B．
7．【解答】解：由图可得，
P1到P5顺时针，P5到P9逆时针，每8个点为一周期循环，
∵（2024﹣1）÷8＝252…7，
∴点P2024落在射线OC上，
故选：C．
8．【解答】解：∵﹣6+8﹣10+12﹣14+16﹣18+20＝8，
∴横、竖、外圈、内圈的4个数之和为4，
∴﹣14+12+16+a＝4，
∴a＝﹣10，
∵12+8+a+c＝4，b+16﹣14+d＝4，
∴c＝﹣6，b+d＝2，
∴b＝﹣18或b＝20，
当b＝﹣18时，d＝20，此时a+b＝﹣10﹣18＝﹣28，
当b＝20时，d＝﹣18，此时a+b＝﹣10+20＝10．
∴a+b的值为﹣28或10．
故选：B．
二．填空题（共5小题）
9．【解答】解：①OC在∠AOB内部时，
∵∠AOB＝50°，∠BOC＝30°，
∴∠AOC＝20°，
∵OM平分∠AOC，
∴∠COM＝10°，
∴∠BOM＝∠COM+∠BOC＝10°+30°＝40°．
②OC在∠AOB外部时，
∵∠AOB＝50°，∠BOC＝30°，
∴∠AOC＝80°，
∵OM平分∠AOC，
∴∠COM＝40°，
∠BOM＝∠COM﹣∠BOC＝40°﹣30°＝10°．
故答案为：40°或10°．
10．【解答】解：设原计划每小时生产y个零件，则实际每小时生产（y+10）个零件．
根据等量关系列方程得：12（y+10）＝13y+60．
故答案为：12（y+10）＝13y+60．
11．【解答】解：由题意可知，MN＝3AB．
∵MN＝m﹣n＝10﹣（﹣2）＝12，
∴AB＝MN＝4．
故答案为：4．
设点A所表示的数为a，则点B表示的数为（a+4），
∴NA＝|a﹣（﹣2）|＝|a+2|，BM＝|a+4﹣10|＝|a﹣6|，
∴|a+2|：|a﹣6|＝3：1，即|a+2|＝3|a﹣6|．
当a＜﹣2时，﹣（a+2）＝﹣3（a﹣6），解得a＝10（不符合题意，舍去）；
当﹣2≤a＜6时，a+2＝﹣3（a﹣6），解得a＝4；
当a≥6时，a+2＝3（a﹣6），解得a＝10．
综上，点A所表示的数为4或10．
故答案为：4或10．
12．【解答】解：设∠A′EG＝x°，
由折叠得：∠A′EG＝∠HEG＝x°，
∵∠FEH＝15°，
∴∠A′EF＝∠A′EG+∠HEG+∠FEH＝（2x+15）°，
由折叠得：∠AEF＝∠A′EF＝（2x+15）°，
∵∠AEF+∠HEG+∠FEH＝180°，
∴2x+15+x+15＝180，
解得：x＝50，
∴∠AEF＝（2x+15）°＝115°，
故答案为：115°．
13．【解答】解：（1）w＝[|1﹣2|+（1+2）]×
＝[|﹣1|+3]×
＝（1+3）×
＝4×
＝2；
（2）W＝[丨|x+4|﹣|x﹣3|丨+（|x+4|+|x﹣3|）]×＝26，
∴丨|x+4|﹣|x﹣3|丨+（|x+4|+|x﹣3|）＝52，
①当x＜﹣4时，
丨|x+4|﹣|x﹣3|丨+（|x+4|+|x﹣3|）＝52，
﹣x﹣4+x﹣3﹣x﹣4+3﹣x＝52，
7﹣2x﹣1＝52，
﹣2x＝46，
x＝﹣23
x＝﹣23，a＝19，b＝26，
∴a+2b＝19+2×26＝71．
②当﹣4≤x＜3时，
丨|x+4|﹣|x﹣3|丨+（|x+4|+|x﹣3|）＝52，
x+4+x﹣3+x+4+3﹣x＝52，
x＝22（不符合条件舍去），
③当3≤x时，
丨|x+4|﹣|x﹣3|丨+（|x+4|+|x﹣3|）＝52，
x+4﹣x+3+x+4+x﹣3＝52，
x＝22，a＝26，b＝19，
∴a+2b＝26+2×19＝64．
综上分析，a+2b的值为92或64．
故答案为：71或64．
三．解答题（共10小题）
14．【解答】解：（1）∵AB＝15，AC＝6，
∴BC＝9，
∵点N是BC的中点，
∴CN＝BN＝BC＝4.5；
（2）∵点M是AB的中点，
∴BM＝AB＝7.5，
∵MN＝BM﹣BN，
∴MN＝3．
15．【解答】解：（1）2×4＝8（万顶），
8÷（3﹣2）＝8（天），
3×8＝24（万顶），
答：这批帐篷一共有24万顶．
（2）2+2×90%＝3.8（万顶），
3+3×m%＝3+3m%（万顶），
24÷3＝8（万顶），
8﹣3.8＝4.2（万顶），
∴3+3m%＝4.2，
解得m＝40，
答：m的值为40．
16．【解答】解：（1）①∵点A、C、E处分别写2、﹣5、0，
∴点F处的数＝2+（﹣5）+0＝﹣3，
故答案为：﹣3；
②∵点A、B、C处分别写3、4、7，
∴点D处的数＝4﹣3﹣7＝﹣6，
故答案为：﹣6；
（2）如图：
设点E、F、G、H处分别写的数为e，f，g，h，
由题意得：e＝h+g+f①，
h＝2024+23+e②，
g＝e+23+1③，
f＝2024+1+e④，
∴②+③+④得：h+g+f＝2×2024+2×23+1×2+2e，
∴e＝2×2024+2×23+1×2+2e，
解得：e＝﹣2048，
∴E点处的数为﹣2048；
（3）顶点D、F处的数相加和为0，
理由：如图：
设点A、B、C、D、E、F、G、H处分别写的数为a，b，c，d，e，f，g，h，
由题意得：d＝b+h+g①，
b＝a+d+c②，
h＝a+e+d③，
g＝c+d+e④，
f＝e+a+c⑤，
把②③④代入①得：d＝a+d+c+a+e+d+c+d+e，
∴d＝2a+3d+2e+2c，
∴2a+2d+2e+2c＝0，
∴a+d+e+c＝0，
∴d+f＝0，
∴顶点D、F处的数相加和为0．
17．【解答】解：（1）如图1，由于射线OE是∠AOD的“好线”，
当∠DOE+∠AOD＝180°时，
∵∠AOD+∠BOD＝180°，
∴∠DOE＝∠BOD＝26°，
∵OC⊥OD，
∴∠COD＝90°，
∴∠COE＝90°﹣26°＝64°，
故答案为：64；
（2）若OE恰好平分∠AOC，
∴∠AOE＝∠COE＝∠BOD，
∴∠BOD＝×（180°﹣90°）＝30°；
（3）∠EOF＝2∠DOG或∠EOF+∠DOG＝45°，理由如下：
如图2﹣1，由于射线OE是∠AOD的“好线”，
当∠AOE+∠AOD＝180°时，
∵∠AOD+∠BOD＝180°，
∴∠AOE＝∠BOD，
∵OF是∠AOE的平分线，
∴∠EOF＝∠AOE＝∠BOD，
∴OG是∠BOC的平分线，
∴∠BOG＝∠BOC＝×（90°+∠BOD）＝45°+∠BOD，
∴∠DOG＝∠BOG﹣∠BOD＝45°﹣∠BOD，
∴∠EOF+∠DOG＝45°，
如图2﹣2，由于射线OE是∠AOD的“好线”，
当∠AOE+∠AOD＝180°时，
∵∠AOD+∠EOD＝180°，
∴∠DOE＝∠BOD，
∴∠DOG＝∠BOC﹣∠BOD
＝（90°+∠BOD）﹣∠BOD
＝45°﹣∠BOD，
∠EOF＝∠AOE＝×（180°﹣2∠BOD）
＝90°﹣∠BOD，
∴∠EOF＝2∠DOG，
综上所述∠EOF＝2∠DOG或∠EOF+∠DOG＝45°．
18．【解答】解：（1）∵∠AOB是直角，∠AOC＝40°，
∴∠AOB+∠AOC＝90°+40°＝130°，
∵OM是∠BOC的平分线，ON是∠AOC的平分线，
∴，．
∴∠MON＝∠MOC﹣∠NOC＝65°﹣20°＝45°，
（2）当锐角∠AOC的大小发生改变时，∠MON的大小不发生改变．
∵＝，
又∠AOB是直角，不改变，
∴．
19．【解答】解：设天头长为6x cm，地头长为4x cm，则左、右边的宽为x cm，
根据题意得，96+（6x+4x）＝4×[26+（6x+4x）×2]，
解得x＝4，
答：边的宽为4cm，天头长为24cm．
20．【解答】解：（1）根据正方体的表面展开图的特征可知，①③④可以折成无盖的正方体，
故答案为：①③④；
（2）①图1所折成的盒子的底面是边长为（a﹣2b）cm的正方形，因此长方体纸盒的底面周长4×（a﹣2b）＝（4a﹣8b）cm，
故答案为：（4a﹣8b）；
②由题意可知，所作出的长方体的长为a﹣2b＝20cm，宽为＝10cm，高为5cm，
所以体积为20×10×5＝1000（cm3），
故答案为：1000；
（3）要使长方体表面展开图的外围周长最大，则剪开的棱越长越好，即没有剪开的棱越短越好，如图所示，其展开图的周长最大，
所以最大周长为58cm．
故答案为：58，没有剪开的棱越短越多，展开图的周长越大．
21．【解答】解：（1）∵线段AB＝24，点C是线段AB的中点，
∴AC＝BC＝＝12，
∵，
∴CD＝BC＝×12＝3；
（2）∵点D在线段AB上，AB＝21a，AD：BD＝3：4，
∴AD＝9a，BD＝12a，
∵AB＝21a，AC＝2BC，
∴AC＝14a，BC＝7a，
∴CD＝AC﹣AD＝14a﹣9a＝5a；
故线段CD的长度为5a．
22．【解答】解：（1）设甲商品件数为x件，
根据题意得：25x+60（2x+15）＝3800，
解得：x＝20，
2x+15＝2×20+15＝55（件），
答：甲商品购进20件，乙商品购进55件；
（2）根据题意，该零售店共获利：50×20×（1﹣10%）×0.9﹣25×20+（0.85×100﹣60）×55＝1685（元），
答：这批商品全部售出后，该零售店共获利1685元．
23．【解答】解：（1）如图1，
∵OC垂直OB，
∴∠BOC＝90°，
∴∠AOC＝∠AOB﹣∠BOC＝30°，
∵OM平分∠COA，
∴∠COM＝15°，
∴∠MOB＝∠BOC+∠COM＝105°；
故答案为：105°；
（2）如图2﹣1，当OC在OB的左侧时，设∠BOC＝α，则∠AOC＝120°+α，
由题意可知，α+120°+α＝180°，
解得α＝30°；
如图2﹣2，当OC在OB的左侧时，设∠BOC＝α，则∠AOC＝α﹣120°，
由题意可知，α+α﹣120°＝180°，
解得α＝150°；
综上，符合题意的∠BOC的度数为30°或150°；
（3）如图3﹣1，3﹣2（OA已停止），OB为∠A′OC的平分线时，
由题意可知，60°﹣1°t＝120﹣5°t，或1°t﹣60°＝60°，
解得t＝15或120；
如图3﹣3，OA′为∠BOC的平分线时，2（5°t﹣120°）＝60°﹣t，
解得t＝；
如图3﹣4，OC为∠A′OB的平分线时，5°t﹣120°＝2（60°﹣1°t），
解得t＝；
故答案为：15或120或或．，未﹣10
坚
持
不
0
x﹣5
2x+2
﹣18
懈
题号
1
2
3
4
5
6
7
8
答案
D
C
B
D
A
B
C
B