中考数学专题训练：几何探究压轴题

这是一份中考数学专题训练：几何探究压轴题，共12页。试卷主要包含了【问题提出】，如图，和的顶点重合，，，，等内容，欢迎下载使用。

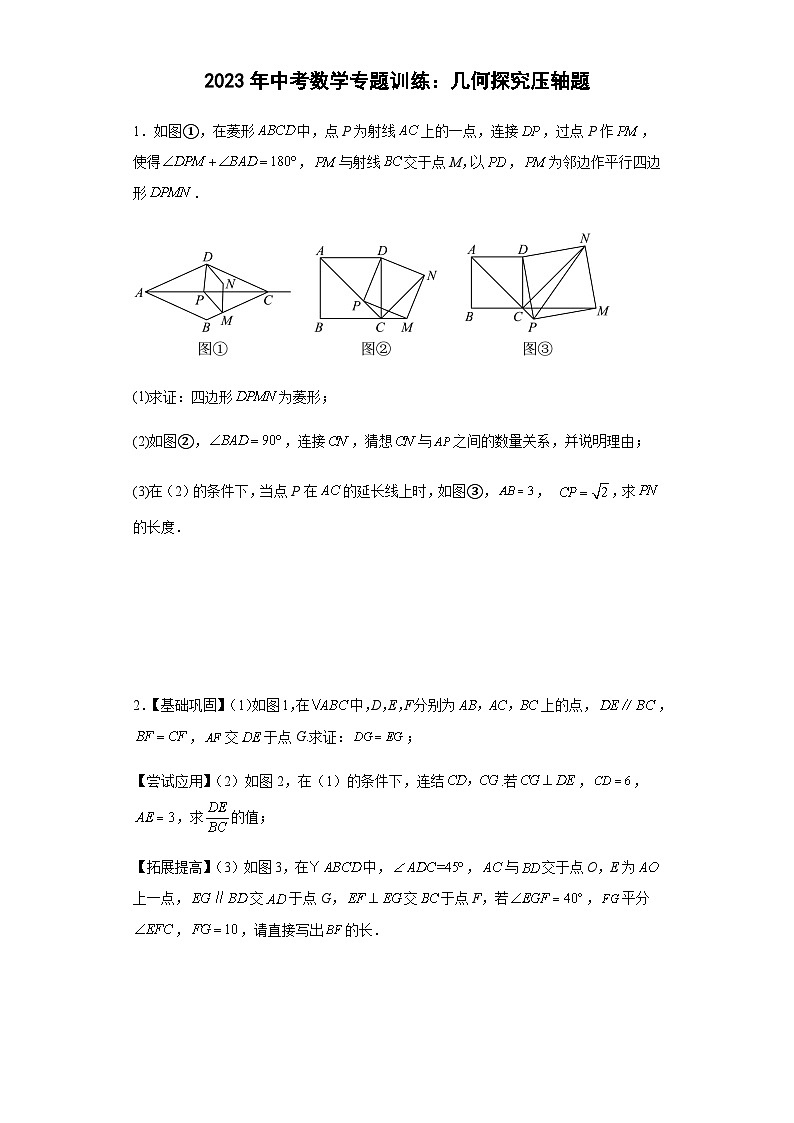
(1)求证：四边形为菱形；
(2)如图②，，连接，猜想与之间的数量关系，并说明理由；
(3)在（2）的条件下，当点P在的延长线上时，如图③，， ，求的长度．
2．【基础巩固】（1）如图1，在中，D，E，F分别为上的点，，，交于点G.求证：；
【尝试应用】（2）如图2，在（1）的条件下，连结.若，，，求的值；
【拓展提高】（3）如图3，在中，，与交于点O，E为上一点，交于点G，交于点F，若，平分，，请直接写出的长．
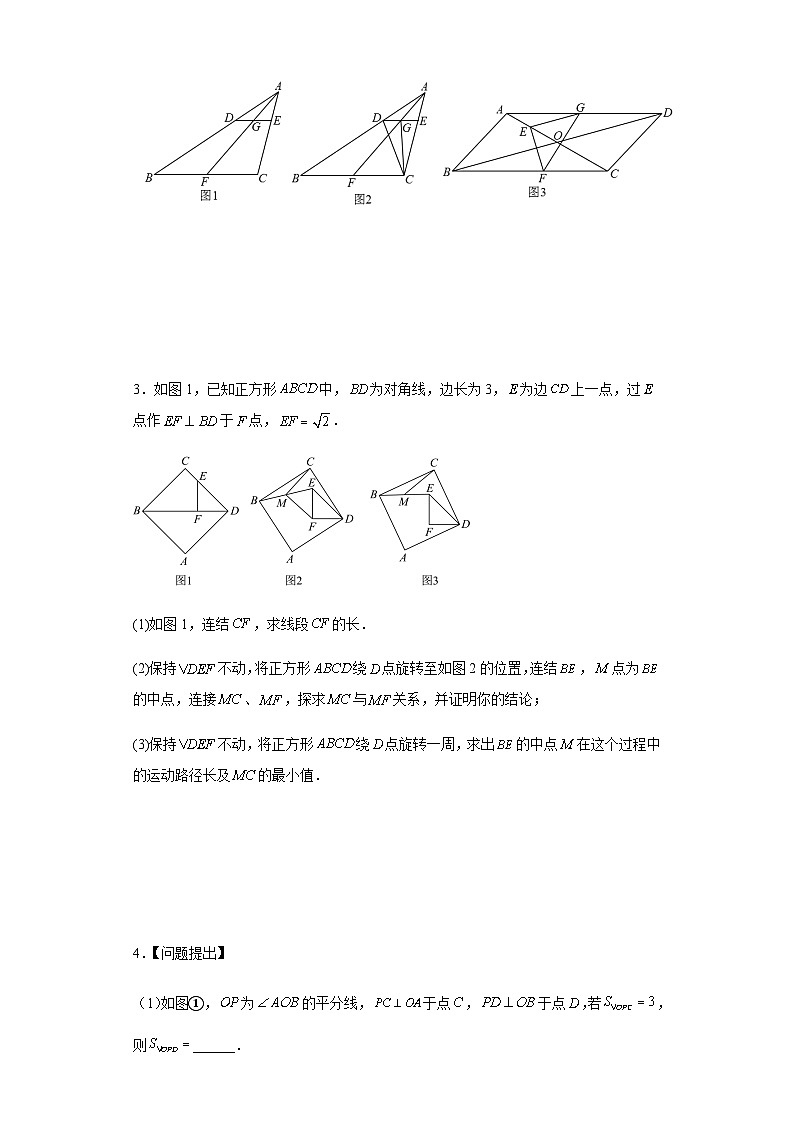
3．如图1，已知正方形中，为对角线，边长为3，为边上一点，过点作于点，．
(1)如图1，连结，求线段的长．
(2)保持不动，将正方形绕点旋转至如图2的位置，连结，点为的中点，连接、，探求与关系，并证明你的结论；
(3)保持不动，将正方形绕点旋转一周，求出的中点在这个过程中的运动路径长及的最小值．
4．【问题提出】
（1）如图①，为的平分线，于点，于点，若，则______．
【问题探究】
（2）如图②，、是两条平行的直线，且、之间的距离为12，点为直线上一点，点、为直线上两点，且点在点的左侧，若，求的最小值；
【问题解决】
（3）如图③，四边形是园林规划局欲修建的一块平行四边形园林的大致示意图，沿对角线修一条人行走道，沿的平分线（点在上）修一条园林灌溉水渠．根据规划要求，，米，且使得平行四边形的面积尽可能小，问平行四边形的面积是否存在最小值？若存在，求出其最小值，若不存在，请说明理由．
5．在和中，，，如图（1），以为边作平行四边形，以为边作平行四边形，点F，G分别是的中点，当绕点C旋转时，
(1)证明：；
(2)①求的面积（用含a，b的代数式表示）；
②直接写出的长度的最大值为（用含a，b的代数式表示）．
6．如图，在边长为6的正方形中，点P是边上一动点，连接，将沿翻折，点A的对应点为点E，连接．
(1)如图1，当时，直接写出的度数为___________；
(2)如图2，过点E作，当时，
①求的长；
②求证：；
(3)如图3，点M是边上一动点，当时，求的最小值．
7．如图1，在与中，，，交于点，，点在线段上，连接．
(1)若，求线段的长；
(2)如图2，若，点为线段的中点，连接，证明：；
(3)如图3，在（2）的条件下，将绕点旋转得，连接，点为线段的中点，连接，当长度取最小时，在线段上有一动点，连接，将线段绕点逆时针旋转60°至，连接，若，请直接写出的最小值．
8．正方形 ，点E为平面内一点，连接，将绕点B顺时针旋转得到 ，连接，．已知点M为的中点，连接．
(1)如图1，①若点E为边边上一点，补全图形；
②判断并证明线段和的数量关系．
(2)如图2，若点E是的内部一点，（1）中线段和的数量关系是否仍然成立，如果成立，请证明；如果不成立，请说明理由．
9．【操作一】如图①，将矩形沿过点D的直线折叠，使点A的对称点F落在边上，折痕为DE．则的大小为 度．
【操作二】如图①，在操作一的基础上，将矩形沿过点C的直线折叠，点B的对称点H落在边上，折痕为．求证：．
【应用】如图②，延长图①中的交边于点M．若，则EH的长为 ，点M到边的距离为 ．
【拓展】如图③，点N为【操作二】图①中的边DE上的点，连结、．若，，则的最小值为 ．
10．如图，和的顶点重合，，，，．
(1)如图1，当点，分别在，上时，得出结论： ；直线与直线的位置关系是 ；
(2)如图2，将图1中的绕点顺时针旋转一周的过程中，连接，，其所在直线相交于点．
①（1）中的结论是否仍然成立，若成立，请证明，若不成立，说明理由．
②当的长度最大时，求线段的长度．
11．如图，为的角平分线．
(1)如图，若于点，交于点，，则______．
(2)如图，若，点在上，且，，，求的长；用含、的式子表示
(3)如图，，点在的延长线上，连接，若的面积是，求的面积．
12．在中，，，过点A作的垂线，垂足为D，E为射线上一动点（不与点C重合），连接，以点A为中心，将线段逆时针旋转得到线段，连接，与直线交于点G．
(1)如图1，当点E在线段上时，
①依题意补全图形；
②求证：点G为的中点．
(2)如图2，当点E在线段的延长线上时，用等式表示之间的数量关系，并证明．
13．在中，，直线经过点C，且于D，于E．
(1)当直线绕点C旋转到图1的位置时，求证：
①；
②．
(2)当直线绕点C旋转到图2的位置时，求证：；
(3)当直线绕点C旋转到图3的位置时，试问具有怎样的等量关系？请写出这个等量关系，并加以证明．
14．如图1，我们把对角线互相垂直的四边形叫做垂美四边形．
(1)判断：在平行四边形、矩形、菱形、正方形中，一定是垂美四边形的有 ；
(2)如图2，垂美四边形两组对边、与、之间有怎样的数量关系？写出你的猜想，并给出证明；
(3)如图3，分别以的直角边和斜边为边向外作正方形和正方形，连接、、，与交于点O，已知，，求的中线的长．
15．新定义：垂直于图形的一边且等分这个图形面积的直线叫作图形的等积垂分线，等积垂分线被该图形截的线段叫做等积垂分线段．
问题探究：
(1)如图1，等边边长为3，垂直于边的等积垂分线段长度为______；
(2)如图2，在中，，，，求垂直于边的等积垂分线段长度；
(3)如图3，在四边形中，，，，求出它的等积垂分线段长．
16．如图1，在矩形中，，，E是边上的一点，连接，将矩形沿折叠，顶点D恰好落在边上的点F处，延长交的延长线于点G．
(1)求线段的长：
(2)求证：四边形为菱形；
(3)如图2，M，N分别是线段上的动点（与端点不重合），且，设，是否存在这样的点N，使是直角三角形？若存在，请求出x的值；若不存在，请说明理由．
17．如图，和均为等腰直角三角形，，，．现将绕点旋转．
(1)如图1，证明：；
(2)如图2，若A，，三点共线，，求点到直线的距离；
(3)如图3，连接，，，求证：．
18．如图，点E，F分别在正方形的边，上，且，点P在射线上（点P不与点F重合）．将线段绕点E顺时针旋转得到线段，过点E作的垂线，垂足为点H，交射线于点Q．
(1)如图1，若点E是的中点，点P在线段上，请直接写出线段，，满足的数量关系______．
(2)如图2，若点E不是的中点，点P在线段上，判断（1）中的结论是否仍然成立，若成立，请写出证明过程；若不成立，请说明理由．
(3)正方形的边长为9，，，请直接写出线段的长______．