专题04 中考数学动点问题中分类讨论、数形结合思想-中考数学三轮冲刺课件

这是一份专题04 中考数学动点问题中分类讨论、数形结合思想-中考数学三轮冲刺课件，共37页。PPT课件主要包含了分类讨论思想概述，数形结合思想概述，典型例题剖析，思想方法总结，分类讨论等内容，欢迎下载使用。
近三年河南中考数学试题相关特点
★2017年~2019年三年的数学试题第15题，第22题，第23题均用到分类讨论方法解答；★除了圆、三角函数需要数形结合解题外，2019年的河南卷第21题更是创新性地推出了反比例函数的研究性题目，充分体现了数形结合的思想，借助函数图象研究函数性质。
所谓数学分类讨论方法，就是将数学对象分成几类，分别进行讨论来解决问题的一种数学方法。有关分类讨论思想的数学问题具有明显的逻辑性、综合性、探索性，能训练人的思维条理性和概括性。
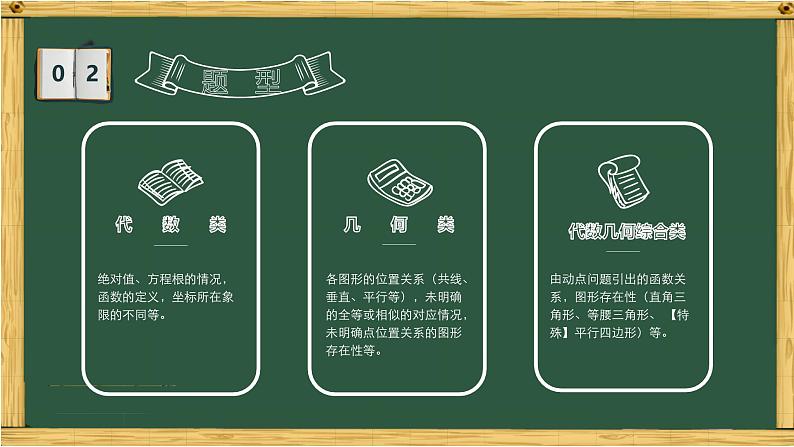
绝对值、方程根的情况，函数的定义，坐标所在象限的不同等。
分类是按照数学对象的相同点和不同点，将其区分为不同种类。正确的分类必须是周全的，既不重复，也不遗漏。分类的原则：①分类中的每部分都是相互独立的；②一次分类按一个标准；③分类讨论应逐级有序进行；④以性质、公式、定理等的使用条件为标准进行分类。
数形结合思想是初中数学解题中一种重要思想，它包括【以形助数】【以数助形】【数形互相转化】三个方面。利用数形结合思想可使很多复杂问题简单化，抽象问题具体化，它具有严谨性与直观性两大优势，是中考解题过程中一个重要途径。
【2020年河南省名校模拟】
【剖析】分成：PA=PF，PA=AF，PF=AF三种情况讨论由折叠性质及勾股定理得：AF=AD=15，EF=DE，BF=9，CF=6，（1）PA=AF，由AB⊥PF，PB=BF=9；（2）PF=AF，则PB=15-9=6；（3）AP=PF，则AP2=PB2+AB2，解得BP=3.5.
【2020年开封市名校联考】
【剖析】（1）确定点P的运动轨迹，是以E为圆心，BE长为半径的圆弧上；（2）矩形边的垂直平分线有两条，这两条直线与P点轨迹交点即为B的落点；（3）确定出落点（4个），作出折痕（F不在射线BA上的排除），利用【勾股定理】【相似三角形】【三角函数】等求解。
【2020年新乡市模拟】
【2020年商丘市一模】
【2020年洛阳市模拟】
【剖析】Rt△ABC有两条直角边，故分两种情况讨论：（1）A’D⊥AC，如图所示，（2）A’D⊥BC
【2020年河南省实验中学模拟】
【剖析】（1）待定系数法求出k值.（2）分成△ADP∽△AOB、△PDA∽△AOB两种情况，根据相似三角形的性质分别求出点P的坐标，代入反比例函数解析式，判断即可．
【剖析】（1）待定系数法求解；（2）分P在x轴上方和P在x轴下方两种情况讨论，得到方程求解；（3）分△BMN∽△AOC和△NMB∽△AOC，得到BM、MN的比例关系，进而构造一线三直角求出N点坐标及M点坐标.
（3）分△NMB∽△AOC和△BMN∽△AOC，① △NMB∽△AOC ，则MN=3BM，如图所示，BT=1，QM=3BT=3，MT=x，则QN=3x，N点坐标为（2+3x，x+3），代入抛物线解析式，求解即可（舍去不合要求的值）② △BMN∽△AOC，同理求解.
剖析（1）待定系数法求解抛物线解析式；（3）分OD为边和OD为对角线两种情况讨论
【2020年开封市一模】
剖析（1）待定系数法求解抛物线解析式；（2）分△PCE∽△OAD，和△CPE∽△OAD两种情况讨论.
【2020年商丘市模拟】
剖析（1）依题意设抛物线解析式为y＝ax（x﹣4），把B（5，5）代入求得解析式；（2）分两种情况讨论，由相似三角形的性质列出等式，即可求解．
【2020年禹州市模拟】
剖析（1）待定系数法代入求得解析式；（2）①将M、P点坐标利用位置关系转变成代数关系，即PM的长度用P点横坐标表示出来，利用函数思想求出最值；②分PM=PC和PM=CM两种情况讨论。
【2020年河南省模拟】
（1）要按照统一标准对问题中的相关条件进行分类。（2）分类讨论条件要明确，内容要完整，必须无重复，无遗漏。（3）如果分类讨论不能够一次性解决题目，就必须以题设情况条件根据不同标准逐级进行分类讨论。