





所属成套资源:中考数学三轮冲刺课件
专题08 数学思想在动点存在性问题中的综合体现-中考数学三轮冲刺课件
展开
这是一份专题08 数学思想在动点存在性问题中的综合体现-中考数学三轮冲刺课件,共24页。PPT课件主要包含了解决此类问题方式方法,函数图象题型,典例剖析,函数思想,折叠问题题型,分类讨论数形结合,存在性问题题型,其它题型,数形结合方程思想等内容,欢迎下载使用。
河南中考数学试题相关特点
★ 动点与存在性问题的考查是多方面的。比如:2017年考查了折叠与直角三角形存在性,动点与函数图象,动点与面积最值,动点与相似三角形存在性等(分值超过了23分);2018年考查了折叠与直角三角形存在性,动点与函数图象,动点与特殊平行四边形存在性,动点与平行四边形存在性及角度存在性等问题(分值超过了22分);2019年考查了折叠与落点问题,动点与菱形存在性,动点与直角三角形存在性等问题,(分值超过了20分).
充分利用已知条件,发掘出有用信息,借助分类讨论、数形结合、函数与方程的思想进行解答,而对于较为复杂问题,要善于利用转化思想,将其转化为比较容易或熟悉的问题解答。综合来说,函数与方程是解题的核心,转化思想是解题的钥匙,数形结合、分类讨论是解题的支柱,勾股定理、相似、三角函数是解题的工具。
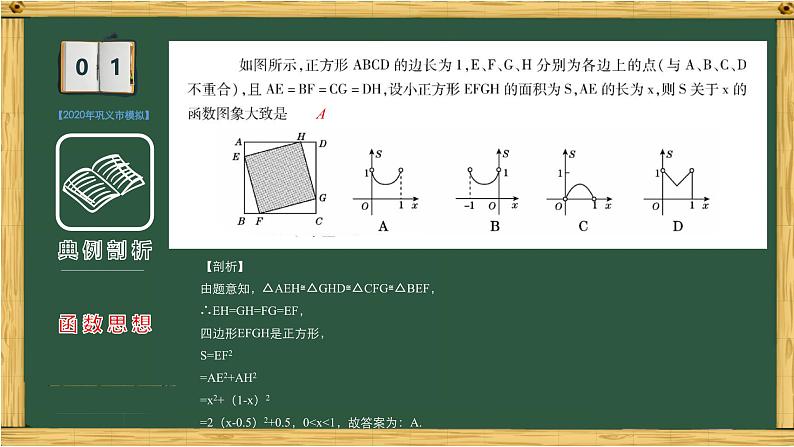
【2020年巩义市模拟】
【剖析】由题意知,△AEH≌△GHD≌△CFG≌△BEF,∴EH=GH=FG=EF,四边形EFGH是正方形,S=EF2=AE2+AH2=x2+(1-x)2=2(x-0.5)2+0.5,0
相关课件
这是一份专题05 转化思想在数学解题中的妙用-中考数学三轮冲刺课件,共38页。PPT课件主要包含了转化思想概述,转化思想适用场景,典型例题剖析,转化思想方法总结等内容,欢迎下载使用。
这是一份专题04 中考数学动点问题中分类讨论、数形结合思想-中考数学三轮冲刺课件,共37页。PPT课件主要包含了分类讨论思想概述,数形结合思想概述,典型例题剖析,思想方法总结,分类讨论等内容,欢迎下载使用。
这是一份2024河南中考数学专题复习 动点综合训练 课件,共48页。









