证明角相等-中考数学三轮冲刺课件

这是一份证明角相等-中考数学三轮冲刺课件，共15页。PPT课件主要包含了∠1+∠290º，∠2∠3，∠1+∠390º，2对顶角相等，DFEC，∠ABD∠ABC等内容，欢迎下载使用。
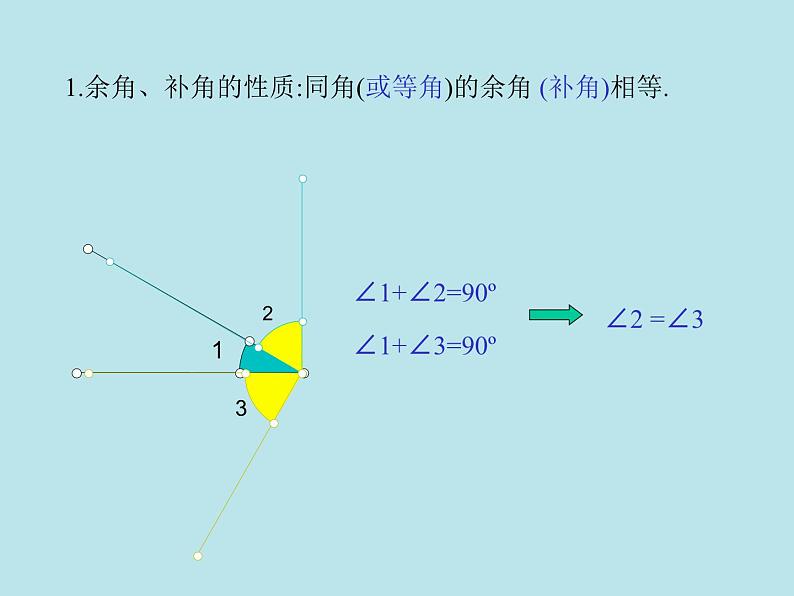
1.余角、补角的性质:同角(或等角)的余角 (补角)相等.
3.平行线的性质:两直线平行同位角(内错角)相等.
4.三角形外角定理:三角形外角等于和它 不相邻的内角之和.
5.全等三角形的性质:全等三角形对应角相等.
6.等腰三角形的性质:等边对等角;三线合一.
7.直角三角形的性质:在直角三角形中,如果一条直角边是斜 边的一半,则这条直角边所对的角是 30°.
8.角平分线的性质定理的逆定理:到一个角两边距离相等的 点在这个角的平分 线上.
9.平行四边形的性质:平行四边形的对角 相等.
10.菱形的性质:菱形的对角线互相垂直平 分,并且每一条对 角线平分一组对角.
11.等腰梯形的性质定理:等腰梯形同一底上 的两个角相等.
12.相似三角形的性质:相似三角形对应角相等.
13.圆心角定理:在同圆或等圆中, 如果两个圆心角, 两条弧,两 条弦或两条弦的弦心距中,有一组量相等,那么它们所对应 的其余各组量都分别相等
14..圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
推论:同弧或等弧所对的圆周角相等,直径所 对的圆周角是直角.
15.圆内接四边形的性质:圆内接四边形的对角互补;并且每一个外 角都等于它的内对角.
16.弦切角定理:弦切角等于所夹弧所对的圆周角
17:两个弦切角所夹的弧相等,这两个弦切角相等.
18.三角形的内心的性质:三角形的内心与角顶点的连线平分这个角.
19.正多边形的性质:正多边形的外角等于它的中心角.
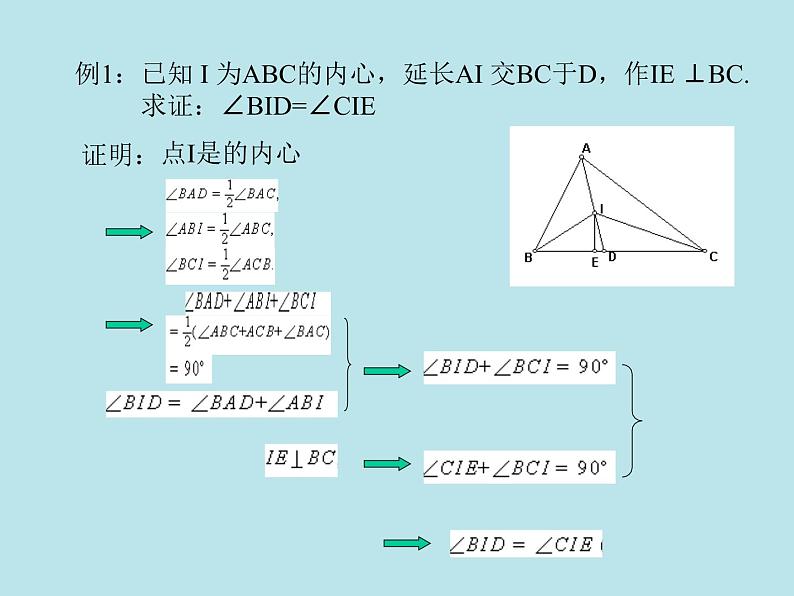
已知 I 为ABC的内心，延长AI 交BC于D，作IE ⊥BC.求证：∠BID=∠CIE
点I是的内心
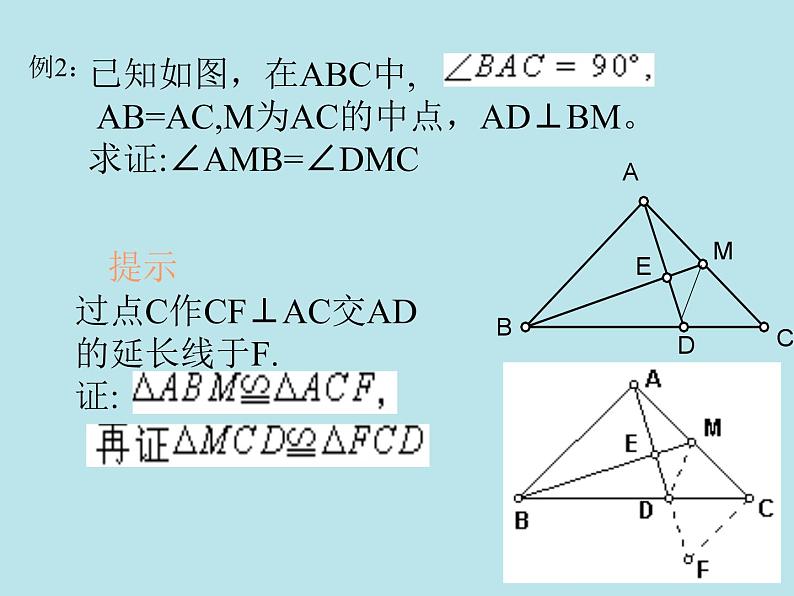
已知如图，在ABC中, AB=AC,M为AC的中点，AD⊥BM。求证:∠AMB=∠DMC
过点C作CF⊥AC交AD的延长线于F.证:
已知，如图，在四边形ABCD中，AB=DC，E、F分别为BC、AD的中点，BA、CD的延长线分别与EF的延长线交于H、G.求证：∠BHE=∠CGE
连结BD，取BD的中点M，连结FM、EM.只需证FM=EM，即可证得∠BHE=∠CGE.
AB是 ⊙O的直径，弦CD⊥AB于E，M是上任意一点。延长AM与DC的延长线交于F。求证：∠FMC=∠AMD
要证∠FMC=∠AMD 而∠FMC是圆内接四边形ABCM的外角，所以∠FMC=∠ABC
已知条件有直径与弦互相垂直，可考虑用垂径定理。
已知 ⊙O1 与 ⊙O2相交于A、B两点，⊙O1的弦BC交⊙O2于E，⊙O2的弦BD交⊙O1于F，且FD=EC。求证：∠ABD=∠ABC
连结AD、AC、AF、AE
∠AFD、∠AEC分别是圆内接四边形AFBC、ADBE的外角
∠AFD=∠ACE，∠AEC=∠ADF
例6：如图，已知BC是直径， ，AD⊥BC， 求证：（1）∠EAF=∠AFE。 （2）BE=AE=EF
例7:已知，两圆内切于M，大圆的弦AB交小圆于C、D两点。求证：∠AMC=∠BMD
1.在△ABC中，EF⊥ AB，CD⊥ AB，G在AC边上并且 ∠GDC=∠EFB，求证: ∠AGD=∠ACB
2.已知，如图，在 △ABC中，AC 2=AD · AB。求证：∠ACD=∠ABC。