广东省2024年中考数学水平提升模拟试题（含解析）

这是一份广东省2024年中考数学水平提升模拟试题（含解析），共20页。试卷主要包含了考生务必保持答题卡的整洁，化简的结果是等内容，欢迎下载使用。
2．答卷前，考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的准考证号、姓名、考场号、座位号．用2B铅笔把对应该号码的标号涂黑．
3．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用像皮檫干净后，再选涂其他答案，答案不能答在试题上．
4．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．
5．考生务必保持答题卡的整洁．考试结束时，将试卷和答题卡一并交回．
一、选择题（本大题10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑．
1．﹣2的绝对值是
A．2 B．﹣2 C． D．±2
【答案】A
【解析】正数的绝对值是它本身，负数的绝对值是它的相反数，0的绝对值是0.
【考点】绝对值
2．某网店2024年母亲节这天的营业额为221 000元，将数221 000用科学记数法表示为
A．2.21×106 B．2.21×105 C．221×103 D．0.221×106
【答案】B
【解析】a×10n形式，其中0≤|a|＜10.
【考点】科学记数法
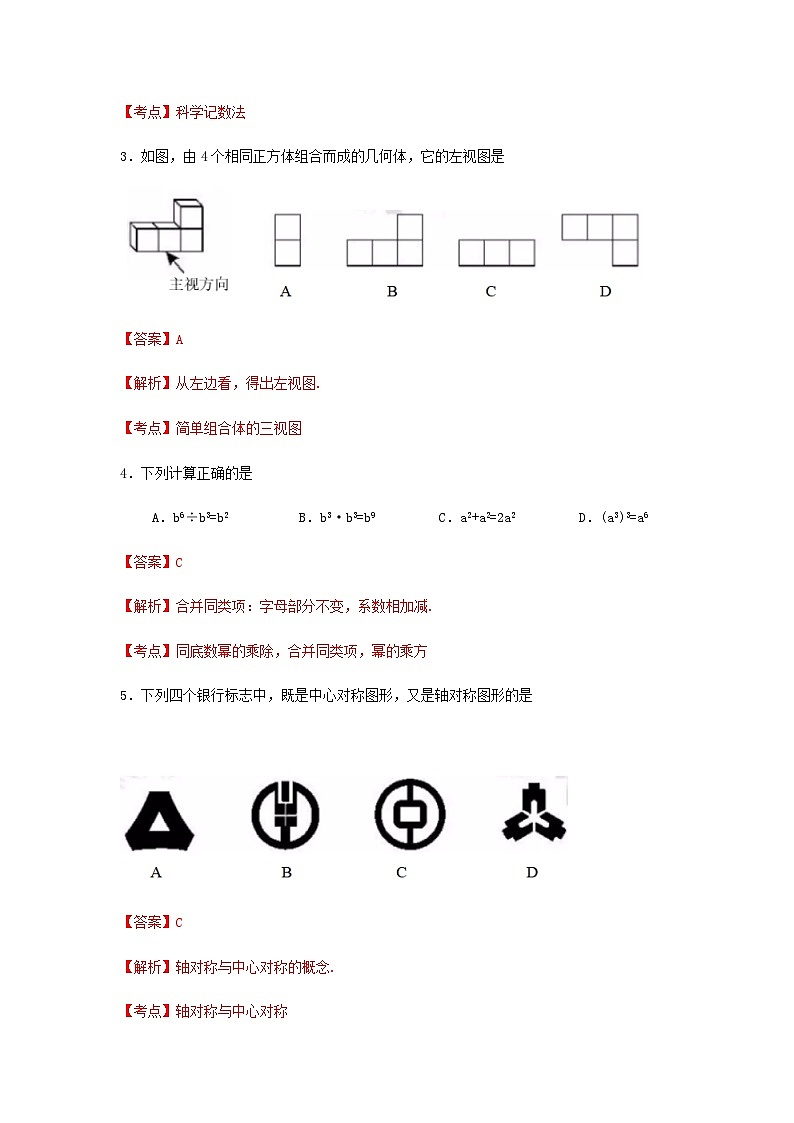
3．如图，由4个相同正方体组合而成的几何体，它的左视图是
【答案】A
【解析】从左边看，得出左视图.
【考点】简单组合体的三视图
4．下列计算正确的是
A．b6÷b3=b2 B．b3·b3=b9 C．a2+a2=2a2 D．(a3)3=a6
【答案】C
【解析】合并同类项：字母部分不变，系数相加减.
【考点】同底数幂的乘除，合并同类项，幂的乘方
5．下列四个银行标志中，既是中心对称图形，又是轴对称图形的是
【答案】C
【解析】轴对称与中心对称的概念.
【考点】轴对称与中心对称
6．数据3、3、5、8、11的中位数是
A．3 B．4 C．5 D．6
【答案】C
【解析】按顺序排列，中间的数或者中间两个数的平均数.
【考点】中位数的概念
7．实数a、b在数轴上的对应点的位置如图所示，下列式子成立的是
A．a>b B．|a|0 D．的x的取值范围；
（2）求这两个函数的表达式；
（3）点P在线段AB上，且S△AOP :S△BOP=1 : 2，求点P的坐标．
【答案】
解：（1）x＜-1或0＜x＜4
（2）∵反比例函数y=图象过点A（﹣1，4）
∴4=，解得k2=﹣4
∴反比例函数表达式为
∵反比例函数图象过点B（4，n）
∴n==﹣1，∴B（4，﹣1）
∵一次函数y=k1x+b图象过A（﹣1，4）和B（4，﹣1）
∴，解得
∴一次函数表达式为y=﹣x+3
（3）∵P在线段AB上，设P点坐标为（a，﹣a+3）
∴△AOP和△BOP的高相同
∵S△AOP :S△BOP=1 : 2
∴AP : BP=1 : 2
过点B作BC∥x轴，过点A、P分别作AM⊥BC，PN⊥BC交于点M、N
∵AM⊥BC，PN⊥BC
∴
∵MN=a+1，BN=4-a
∴，解得a=
∴-a+3=
∴点P坐标为（，）
（或用两点之间的距离公式AP=，BP=，由解得a1=，a2=-6舍去）
【考点】一次函数和反比例函数的数形结合，会比较函数之间的大小关系，会求函数的解析式，同高的三角形的面积比与底边比的关系
24．如题24-1图，在△ABC中，AB=AC，⊙O是△ABC的外接圆，过点C作∠BCD=∠ACB交⊙O于点D，连接AD交BC于点E，延长DC至点F，使CF=AC，连接AF．
（1）求证：ED=EC；
（2）求证：AF是⊙O的切线；
（3）如题24-2图，若点G是△ACD的内心，BC·BE=25，求BG的长．
【答案】
（1）证明：∵AB=AC
∴∠B==∠ACB
∵∠BCD=∠ACB
∴∠B=∠BCD
∵ eq \(\s\up7(⌒),AC)= eq \(\s\up7(⌒),AC)
∴∠B=∠D
∴∠BCD=∠D
∴ED=EC
（2）证明：
连接AO并延长交⊙O于点G，连接CG
由（1）得∠B=∠BCD
∴AB∥DF
∵AB=AC，CF=AC
∴AB=CF
∴四边形ABCF是平行四边形
∴∠CAF=∠ACB
∵AG为直径
∴∠ACG=90°，即∠G+∠GAC=90°
∵∠G=∠B，∠B=∠ACB
∴∠ACB+∠GAC=90°
∴∠CAF+∠GAC=90°即∠OAF=90°
∵点A在⊙O上
∴AF是⊙O的切线
（3）解：
连接AG
∵∠BCD=∠ACB，∠BCD=∠1
∴∠1=∠ACB
∵∠B=∠B
∴△ABE∽△CBA
∴
∵BC·BE=25
∴AB2=25
∴AB=5
∵点G是△ACD的内心
∴∠2=∠3
∵∠BGA=∠3+∠BCA=∠3+∠BCD=∠3+∠1=∠3+∠2=∠BAG
∴BG=AB=5
【考点】圆的综合应用，等弧等弦等角的转换，切线的证明，垂径定理的逆应用，内心的概念，相似三角形的应用，外角的应用，等量代换的意识
25．如题25-1图，在平面直角坐标系中，抛物线y=与x轴交于点A、B(点A在点B右侧)，点D为抛物线的顶点．点C在y轴的正半轴上，CD交x轴于点F，△CAD绕点C顺时针旋转得到△CFE，点A恰好旋转到点F，连接BE．
（1）求点A、B、D的坐标；
（2）求证：四边形BFCE是平行四边形；
（3）如题25-2图，过顶点D作DD1⊥x 轴于点D1，点P是抛物线上一动点，过点P作PM⊥ x轴，点M为垂足，使得△PAM与△DD1A相似（不含全等）．
①求出一个满足以上条件的点P的横坐标；
②直接回答这样的点P共有几个？
【答案】
（1）解：由y==得点D坐标为（﹣3，）
令y=0得x1=﹣7，x2=1
∴点A坐标为（﹣7，0），点B坐标为（1，0）
（2）证明：
过点D作DG⊥y轴交于点G，设点C坐标为（0，m）
∴∠DGC=∠FOC=90°，∠DCG=∠FCO
∴△DGC∽△FOC
∴
由题意得CA=CF，CD=CE，∠DCA=∠ECF，OA=1，DG=3，CG=m+
∵CO⊥FA
∴FO=OA=1
∴，解得m= （或先设直线CD的函数解析式为y=kx+b，用D、F两点坐标求出y=x+，再求出点C的坐标）
∴点C坐标为（0，）
∴CD=CE==6
∵tan∠CFO==
∴∠CFO=60°
∴△FCA是等边三角形
∴∠CFO=∠ECF
∴EC∥BA
∵BF=BO－FO=6
∴CE=BF
∴四边形BFCE是平行四边形
（3）解：①设点P坐标为（m，），且点P不与点A、B、D重合．若△PAM与△DD1A相似，因为都是直角三角形，则必有一个锐角相等．由（1）得AD1=4，DD1=
（A）当P在点A右侧时，m＞1
（a）当△PAM∽△DAD1，则∠PAM=∠DAD1，此时P、A、D三点共线，这种情况不存在
（b）当△PAM∽△ADD1，则∠PAM=∠ADD1，此时
∴，解得m1=（舍去），m2=1（舍去），这种不存在
（B）当P在线段AB之间时，﹣7＜m＜1
（a）当△PAM∽△DAD1，则∠PAM=∠DAD1，此时P与D重合，这种情况不存在
（b）当△PAM∽△ADD1，则∠PAM=∠ADD1，此时
∴，解得m1=，m2=1（舍去）
（C）当P在点B左侧时，m＜﹣7
（a）当△PAM∽△DAD1，则∠PAM=∠DAD1，此时
∴﹣，解得m1=﹣11，m2=1（舍去）
（b）当△PAM∽△ADD1，则∠PAM=∠ADD1，此时
∴﹣，解得m1=，m2=1（舍去）
综上所述，点P的横坐标为，﹣11，，三个任选一个进行求解即可．
②一共存在三个点P，使得△PAM与△DD1A相似．
【考点】二次函数的综合应用，旋转的性质，相似三角形的的应用，等边三角形的性质，平行四边形的证明，平面直角坐标的灵活应用，动点问题，分类讨论思想