新高考数学一轮复习考点分类讲与练第52讲 空间几何体的表面积与体积（2份，原卷版+解析版）

这是一份新高考数学一轮复习考点分类讲与练第52讲 空间几何体的表面积与体积（2份，原卷版+解析版），文件包含新高考数学一轮复习考点分类讲与练第52讲空间几何体的表面积与体积原卷版doc、新高考数学一轮复习考点分类讲与练第52讲空间几何体的表面积与体积解析版doc等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。
知识梳理
1. 空间几何体
(1)多面体
①棱柱：有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体叫棱柱．侧棱与底面垂直的棱柱叫做直棱柱．底面为正多边形的直棱柱叫做正棱柱．
②棱锥：有一个面是多边形，其余各面都是有一个公共顶点的三角形，由这些所围成的几何体叫棱锥．如果棱锥的底面是正多边形，且它的顶点在过底面中心且与底面垂直的直线上，则这个棱锥叫做正棱锥．
③棱台：用一个平行于棱锥底面的平面去截棱锥．底面与截面之间的部分，叫棱台．棱台的各侧棱延长后交于一点．
(2)旋转体
①旋转面：一条平面曲线绕它所在平面内的一条定直线旋转所形成的曲面．
②旋转体：封闭的旋转面围成的几何体．
③圆柱：以矩形的一边所在的直线为旋转轴，其余三边旋转一周形成的曲面所围成的几何体叫圆柱．不垂直于轴的边旋转而成的曲面叫做圆柱的侧面，无论旋转到什么位置，这条边都叫做母线．
④圆锥：以直角三角形的一条直角边所在直线为旋转轴，其余两边旋转形成的曲面所围成的几何体叫做圆锥．
⑤圆台：以直角梯形中垂直于底边的腰所在的直线为旋转轴，将直角梯形旋转一周而形成的曲面所围成的几何体叫做圆台．(或用一个平行于圆锥底面的平面去截圆锥．底面与截面之间的部分，叫做圆台．)圆台的母线延长后交于一点．
⑥球：以半圆的直径所在的直线为旋转轴，半圆面旋转一周所形成的旋转体叫做球体，简称球．经过球面上两点的大圆劣弧的长叫做球面距离．
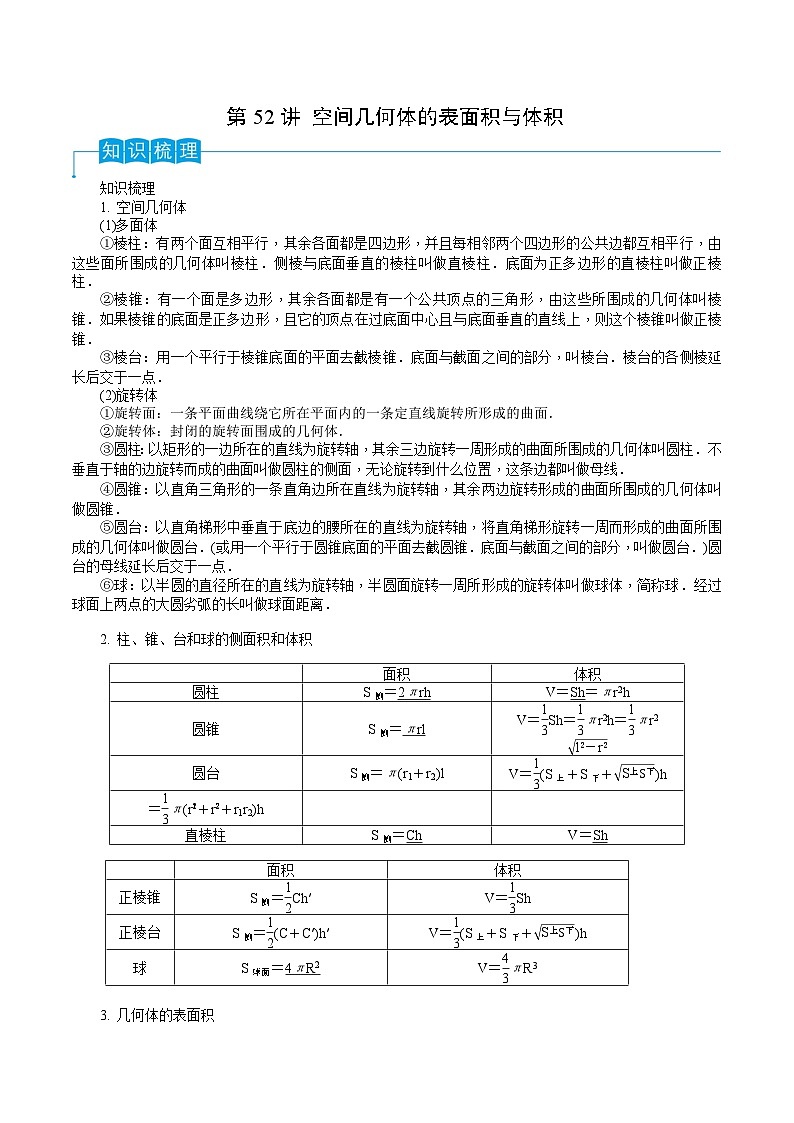
2. 柱、锥、台和球的侧面积和体积
3. 几何体的表面积
(1)棱柱、棱锥、棱台的表面积就是各面面积之和．
(2)圆柱、圆锥、圆台的侧面展开图分别是矩形、扇形、扇环；它们的表面积等于侧面积与底面面积之和．
1、【2022年新高考1卷】南水北调工程缓解了北方一些地区水资源短缺问题，其中一部分水蓄入某水库.已知该水库水位为海拔时，相应水面的面积为；水位为海拔时，相应水面的面积为，将该水库在这两个水位间的形状看作一个棱台，则该水库水位从海拔上升到时，增加的水量约为（）（ ）
A．B．C．D．
【答案】C
【解析】依题意可知棱台的高为(m)，所以增加的水量即为棱台的体积．
棱台上底面积，下底面积，
∴
．
故选：C．
2、【2022年新高考1卷】已知正四棱锥的侧棱长为l，其各顶点都在同一球面上.若该球的体积为，且，则该正四棱锥体积的取值范围是（ ）
A．B．C．D．
【答案】C
【解析】
∵ 球的体积为，所以球的半径,
设正四棱锥的底面边长为，高为，
则，,
所以，
所以正四棱锥的体积，
所以，
当时，，当时，，
所以当时，正四棱锥的体积取最大值，最大值为，
又时，，时，,
所以正四棱锥的体积的最小值为，
所以该正四棱锥体积的取值范围是.
故选：C.
3、【2022年新高考2卷】已知正三棱台的高为1，上、下底面边长分别为和，其顶点都在同一球面上，则该球的表面积为（ ）
A．B．C．D．
【答案】A
【解析】设正三棱台上下底面所在圆面的半径，所以，即，设球心到上下底面的距离分别为，球的半径为，所以，，故或，即或，解得符合题意，所以球的表面积为．
故选：A．
4、【2021年甲卷理科】2020年12月8日，中国和尼泊尔联合公布珠穆朗玛峰最新高程为8848.86（单位：m），三角高程测量法是珠峰高程测量方法之一．如图是三角高程测量法的一个示意图，现有A，B，C三点，且A，B，C在同一水平面上的投影满足，．由C点测得B点的仰角为，与的差为100；由B点测得A点的仰角为，则A，C两点到水平面的高度差约为（）（ ）
A．346B．373C．446D．473
【答案】B
【解析】
【分析】
通过做辅助线，将已知所求量转化到一个三角形中，借助正弦定理，求得，进而得到答案．
【详解】
过作，过作，
故，
由题，易知为等腰直角三角形，所以．
所以．
因为，所以
在中，由正弦定理得：
，
而，
所以
所以．
故选：B．
5、【2021年甲卷理科】已如A，B，C是半径为1的球O的球面上的三个点，且，则三棱锥的体积为（ ）
A．B．C．D．
【答案】A
【解析】
，为等腰直角三角形，，
则外接圆的半径为，又球的半径为1，
设到平面的距离为，
则，
所以.
故选：A.
6、【2021年新高考2卷】正四棱台的上､下底面的边长分别为2，4，侧棱长为2，则其体积为（ ）
A．B．C．D．
【答案】D
【解析】作出图形，连接该正四棱台上下底面的中心，如图，
因为该四棱台上下底面边长分别为2，4，侧棱长为2，
所以该棱台的高，
下底面面积，上底面面积，
所以该棱台的体积.
故选：D.
7、【2020年新课标1卷理科】埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥，以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为（ ）
A．B．C．D．
【答案】C
【解析】如图，设，则，
由题意，即，化简得，
解得（负值舍去）.
故选：C.
8、【2020年新课标1卷理科】已知为球的球面上的三个点，⊙为的外接圆，若⊙的面积为，，则球的表面积为（ ）
A．B．C．D．
【答案】A
【解析】设圆半径为，球的半径为，依题意，
得，为等边三角形，
由正弦定理可得，
，根据球的截面性质平面，
，
球的表面积.
故选：A
1、已知圆锥的表面积等于12π cm2，其侧面展开图是一个半圆，则底面圆的半径为( )

A. 1 cm B. 2 cm C. 3 cm D. eq \f(3,2) cm
【答案】B
【解析】 S表＝πr2＋πrl＝πr2＋πr·2r＝3πr2＝12π，
∴r2＝4，∴r＝2. 故选B.
2、 正四棱锥底面正方形的边长为4，高与斜高的夹角为30°，则该四棱锥的侧面积( )

A. 32 B. 48 C. 64 D. eq \f(32,3)
【答案】 A
【解析】 如图，正四棱锥的高PO，斜高PE，底面边心距OE组成直角三角形POE. 因为OE＝2cm，∠OPE＝30°，所以斜高PE＝eq \f(OE,sin30°)＝4，所以S正棱锥侧＝eq \f(1,2)×4×4×4＝32.故选A.
3、已知圆柱的上、下底面的中心分别为O1，O2，过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为( )
A．12eq \r(2)π B．12π
C．8eq \r(2)π D．10π
【答案】 B
【解析】 设圆柱的轴截面的边长为x，则由x2＝8，得x＝2eq \r(2)，∴S圆柱表＝2S底＋S侧＝2×π×(eq \r(2))2＋2π×eq \r(2)×2eq \r(2)＝12π.
4、（深圳市高级中学集团期末试题）已知圆锥的表面积为3π，它的侧面展开图是一个半圆，则此圆锥的体积为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】求出圆锥的底面半径和圆锥的母线长与高，再计算圆锥的体积．
【详解】解：设圆锥的底面半径为r，圆锥的母线长为l，
由，得，
又，
所以，解得；
所以圆锥的高为，
所以圆锥的体积为．
故选：C．
考向一 空间几何体的的表面积
例1、1．一个正三棱台的上、下底面边长分别是3 cm和6 cm，高是eq \f(3,2) cm．
则三棱台的斜高为 ；三棱台的侧面积为 ；表面积为 ．
2．已知圆柱的底面半径为1，母线长与底面的直径相等，则该圆柱的表面积为________．
3．正六棱柱的底面边长为4，高为6，则它的外接球(正六棱柱的顶点都在此球面上)的表面积为________．
【答案】：1．eq \r(3) cm；eq \f(27\r(3),2) cm2；eq \f(99\r(3),4) cm2 2．6π 3．100π
【解析】：1．设O1、O分别为正三棱台ABC—A1B1C1的上、下底面正三角形的中心，如图所示，则O1O＝eq \f(3,2)，过O1作O1D1⊥B1C1，OD⊥BC，则D1D为三棱台的斜高；
过D1作D1E⊥AD于E，则D1E＝O1O＝eq \f(3,2)，
因O1D1＝eq \f(\r(3),6)×3＝eq \f(\r(3),2)，OD＝eq \f(\r(3),6)×6＝eq \r(3)，则DE＝OD－O1D1＝eq \r(3)－eq \f(\r(3),2)＝eq \f(\r(3),2)．
在Rt△D1DE中，D1D＝eq \r(D1E2＋ED2)＝ ＝eq \r(3)(cm)．
故三棱台斜高为eq \r(3) cm．
设c、c′分别为上、下底的周长，h′为斜高，
S侧＝eq \f(1,2)(c＋c′)h′＝eq \f(1,2)(3×3＋3×6)×eq \r(3)＝eq \f(27\r(3),2) (cm2)，
S表＝S侧＋S上＋S下＝eq \f(27\r(3),2)＋eq \f(\r(3),4)×32＋eq \f(\r(3),4)×62＝eq \f(99\r(3),4) (cm2)．
故三棱台的侧面积为eq \f(27\r(3),2) cm2，表面积为eq \f(99\r(3),4) cm2．
2．该圆柱的侧面积为2π×1×2＝4π，一个底面圆的面积是π，所以该圆柱的表面积为4π＋2π＝6π．
3．依题意，该正六棱柱的外接球的球心应是上、下底面中心连线的中点，因此其半径等于5，其表面积等于4π×25＝100π．
变式1、（1）（江苏省南通市西亭高级中学2019-2020学年高三下学期学情调研）若圆柱的底面直径和高都与球的直径相等圆柱、球的表面积分别记为、则有
（2）（江苏省南通市海安高级中学2019-2020学年高三下学期阶段考试）现有一个橡皮泥制作的圆锥，底面半径为1，高为4.若将它制作成一个总体积不变的球，则该球的表面积为_______.
【答案】（1）（2）
【解析】（1）设球的直径为2R，则
（2）由题意知,圆锥的体积为.设球的半径为
则,解得.所以表面积为.
故答案为:.
变式2、（1）（2022年江苏省淮安市高三模拟试卷）一个圆柱的侧面展开图是一个正方形，则这个圆柱的表面积与侧面积的比值是（ ）
A. B. C. D.
【答案】B
【解析】
【详解】设圆柱的底面半径为，圆柱的高为，
圆柱的侧面展开图是一个正方形，
，
圆柱的侧面积为，
圆柱的两个底面积为，圆柱的表面积为，
圆柱的表面积与侧面积的比为：，
故选：．
（2）（2023·广东·统考一模）已知一个圆锥和圆柱的底面半径和高分别相等，若圆锥的轴截面是等边三角形，则这个圆锥和圆柱的侧面积之比为（ ）
A．B．C．D．
【答案】C
【解析】设圆锥和圆柱的底面半径为，
因为圆锥的轴截面是等边三角形，所以圆锥的母线长为，
则圆锥和圆柱的高为，
所以圆锥的侧面积为，
圆柱的侧面积为，
所以圆锥和圆柱的侧面积之比为,
故选:C.
方法总结：几何体的表面积的求法
(1) 求表面积问题的思路是将立体几何问题转化为平面问题，即空间图形平面化，这是解决立体几何的主要出发点．
(2) 求不规则几何体的表面积时，通常将所给几何体分割成基本的柱、锥、台体，先求这些柱、锥、台体的表面积，再通过求和或作差求得几何体的表面积．
考向二 空间几何体的体积
例2、如图1，在直角梯形ABCD中，∠ADC＝90°，CD∥AB，AB＝4，AD＝CD＝2，将△ADC沿AC折起，使平面ADC⊥平面ABC，得到空间图形D-ABC，如图2所示．
(1) 求证：BC⊥平面ACD；
(2) 求空间图形D-ABC的体积．
图1 图2
【解析】 (1) 由题意，得AC＝BC＝2 eq \r(2)，
所以AC2＋BC2＝AB2，故AC⊥BC.
又平面ADC⊥平面ABC，平面ADC∩平面ABC＝AC，BC⊂平面ABC，
所以BC⊥平面ACD.
(2) 由(1)可知，BC为三棱锥B-ACD的高，BC＝2 eq \r(2)，S△ACD＝2，所以VB-ACD＝ eq \f(1,3)S△ACD·BC＝ eq \f(1,3)×2×2 eq \r(2)＝ eq \f(4\r(2),3)，由等体积性可知，空间图形D-ABC的体积为 eq \f(4\r(2),3).
变式1、（1）（江苏省南通市海安高级中学2019-2020学年高三阶段测试）如图正四棱柱的体积为27，点E，F分别为棱上的点（异于端点）且，则四棱锥的体积为___________.
（2）（江苏省南通市海安高级中学2019-2020学年高三9月月考）已知长方体的体积为，则三棱锥的体积为______.
【答案】（1）9 （2）
【解析】（1）连接，

∵正四棱柱的体积为27，
点E，F分别为棱上的点（异于端点），且，
，
，
∴四棱锥的体积．
故答案为：9．
（2）设长方体的底面积为，高为，
则长方体的体积为，
由题意可知，三棱锥的底面积为，高为，
因此，三棱锥的体积为，故答案为.
方法总结：本题考查空间几何体的体积运算．应注意：(1)若所给定的几何体是柱体、锥体或台体等规则几何体，则可直接利用公式进行求解，其中，等积转换法多用来求三棱锥的体积．(2)若所给定的几何体是不规则几何体，则将不规则的几何体通过分割或补形转化为规则几何体，再利用公式求解．
考向三 与球有关的切、接问题
例3、已知直三棱柱ABC-A1B1C1的6个顶点都在球O的球面上，若AB＝3，AC＝4，AB⊥AC，AA1＝12，则球O的半径为( )
A. eq \f(3\r(17),2) B. 2 eq \r(10)
C. eq \f(13,2) D. 3 eq \r(10)
【答案】 C
【解析】 如图，过球心作平面ABC的垂线，则垂足为BC的中点M.又AM＝ eq \f(1,2)BC＝ eq \f(5,2)，OM＝ eq \f(1,2)AA1＝6，所以球O的半径R＝OA＝ eq \r(\b\lc\(\rc\)(\a\vs4\al\c1(\f(5,2)))\s\up12(2)＋62)＝ eq \f(13,2).
变式1、 (1) 如图，在圆柱O1O2内有一个球O，该球与圆柱的上、下底面及母线均相切．记圆柱O1O2的体积为V1，球O的体积为V2，则 eq \f(V1,V2)的值是________；
【答案】 eq \f(3,2)
【解析】 设圆柱内切球的半径为R，则由题设可得圆柱O1O2的底面圆的半径为R，高为2R，
故 eq \f(V1,V2)＝ eq \f(πR2·2R,\f(4,3)πR3)＝ eq \f(3,2).
(2) 已知正三棱锥的高为1，底面边长为 2 eq \r(3)，内有一个球与四个面都相切，则该正三棱锥的内切球的半径为________．
【解析】 如图，过点P作PD⊥平面ABC于点D，连接AD并延长交BC于点E，连接PE.因为△ABC是正三角形，所以AE是BC边上的高和中线，D为△ABC的中心．因为AB＝2 eq \r(3)，所以S△ABC＝3 eq \r(3)，DE＝1，PE＝ eq \r(2)，所以三棱锥P-ABC的表面积S表＝3× eq \f(1,2)×2 eq \r(3)× eq \r(2)＋3 eq \r(3)＝3 eq \r(6)＋3 eq \r(3).因为PD＝1，所以三棱锥的体积V＝ eq \f(1,3)×3 eq \r(3)×1＝ eq \r(3).设内切球的半径为r，以球心O为顶点，三棱锥的四个面为底面将正三棱锥分割为四个小棱锥，则r＝ eq \f(3\r(3),3\r(6)＋3\r(3))＝ eq \r(2)－1.
【答案】 eq \r(2)－1
变式2、（2020·河南高三期末（文））张衡是中国东汉时期伟大的天文学家、数学家，他曾经得出圆周率的平方除以十六等于八分之五.已知三棱锥的每个顶点都在球的球面上，底面，，且，，利用张衡的结论可得球的表面积为（ ）
A．30B．C．33D．
【答案】B
【解析】
因为，所以，又底面，
所以球的球心为侧棱的中点，
从而球的直径为.
利用张衡的结论可得，则，
所以球的表面积为.
故选：B
变式3、（2020届山东省潍坊市高三上学期统考）已知边长为2的等边三角形，为的中点，以为折痕进行折叠，使折后的，则过，，，四点的球的表面积为（ ）
A．B．C．D．
【答案】C
【解析】
边长为2的等边三角形，为的中点，以为折痕进行折叠，使折后的，构成以D为顶点的三棱锥，且三条侧棱互相垂直，可构造以其为长宽高的长方体，其对角线即为球的直径，三条棱长分别为1,1，，所以，球面积，故选C.
方法总结：解决与球相关的切、接问题的解题要领：(1)球的内切问题主要是指球内切多面体与旋转体，解答时首先要找准切点，通过作截面来解决．如果内切的是多面体，则作截面时主要抓住多面体过球心的对角面来作．(2)把一个多面体的几个顶点放在球面上即为球的外接问题．解决这类问题的关键是抓住外接的特点，即球心到多面体的顶点的距离等于球的半径．
1、（2023·广东广州·统考一模）已知三棱锥的四个顶点都在球的球面上，，，则球的表面积为（ ）
A．B．C．D．
【答案】A
【解析】在三棱锥中，如图，，则，同理，
而平面，因此平面，
在等腰中，，则，，
令的外接圆圆心为，则平面，，
有，取中点D，连接OD，则有，又平面，即，
从而，四边形为平行四边形，，又，
因此球O的半径，
所以球的表面积.
故选：A
2、（2022年广东省高三大联考模拟试卷） 我国古代建筑的屋顶对建筑立面起着特别重要的作用，古代建筑屋顶主要有庑殿式、硬山顶、歇山顶、悬山顶攒尖顶、盝顶、卷棚顶等类型，其中硬山式屋顶造型的最大特点是比较简单、朴素，只有前后两面坡，而且屋顶在山墙墙头处与山墙齐平，没有伸出部分，山面裸露没有变化．硬山式屋顶（如图1）可近似地看作直三棱柱（如图2），其高为，到平面的距离为，为，则可估算硬山式屋顶的体积约为（ ）
A. B. C. D.
【答案】B
【解析】
【详解】解：如图，过作于，
由题意可知，在直三棱柱中，到平面的距离为，
即，又，
所以该柱体体积为.
故选：B.
3、（2022年河北省衡水中学高三模拟试卷）已知一个圆锥的底面半径为3，其侧面积是底面积的2倍，则圆锥的体积为（ ）
A. B. C. D.
【答案】C
【解析】
【详解】解：设圆锥的高为h，母线长为l，则圆锥的侧面积，故，故圆锥的体积．
故选：C．
4、（2022年广东省佛山市高三模拟试卷）已知一圆台高为7，下底面半径长4，此圆台外接球的表面积为，则此圆台的体积为（ ）
A. B. C. D.
【答案】C
【解析】
【详解】
如图为圆台及其外接球的轴截面，为外接球球心，，为等腰梯形的下底和上底的中点，所以，，
因为外接球的表面积为，所以外接球的半径为，圆台下底面半径为4，所以，，则，，即圆台上底面半径为3，所以圆台的体积为.
故选：C.
5、（2023·广东茂名·统考一模）已知菱形ABCD的各边长为2，.将沿AC折起，折起后记点B为P，连接PD，得到三棱锥，如图所示，当三棱锥的表面积最大时，三棱锥的外接球体积为（ ）
A．B．C．D．
【答案】D
【解析】由题意可得：均为边长为2的等边三角形，为全等的等腰三角形，
则三棱锥的表面积，
当且仅当，即时，三棱锥的表面积取最大值，
此时为直角三角形，，
取的中点，连接，由直角三角形的性质可得：，
即三棱锥的外接球的球心为，半径为，故外接球体积为.
故选：D.
面积
体积
圆柱
S侧＝2πrh
V＝Sh＝πr2h
圆锥
S侧＝πrl
V＝eq \f(1,3)Sh＝eq \f(1,3)πr2h＝eq \f(1,3)πr2eq \r(l2－r2)
圆台
S侧＝π(r1＋r2)l
V＝eq \f(1,3)(S上＋S下＋eq \r(S上S下))h
＝eq \f(1,3)π(req \\al(2,1)＋req \\al(2,2)＋r1r2)h
直棱柱
S侧＝Ch
V＝Sh
面积
体积
正棱锥
S侧＝eq \f(1,2)Ch′
V＝eq \f(1,3)Sh
正棱台
S侧＝eq \f(1,2)(C＋C′)h′
V＝eq \f(1,3)(S上＋S下＋eq \r(S上S下))h
球
S球面＝4πR2
V＝eq \f(4,3)πR3