





2025届高考数学二轮总复习专题1函数与导数专项突破1突破2利用导数证明问题课件
展开
这是一份2025届高考数学二轮总复习专题1函数与导数专项突破1突破2利用导数证明问题课件,共24页。
导数与不等式的交汇命题是高考的热点和难点,在利用导数证明不等式的问题中,常用的方法有构造函数、适当换元、合理放缩、利用最值、有界性、不等式及其性质等.
考点一 构造差函数法证明不等式
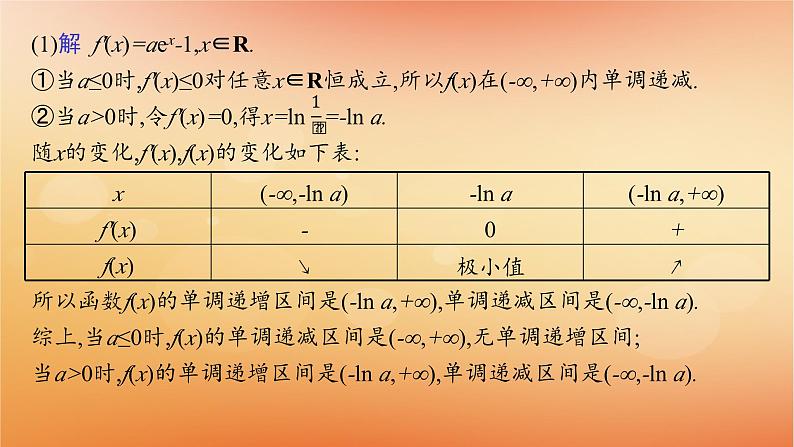
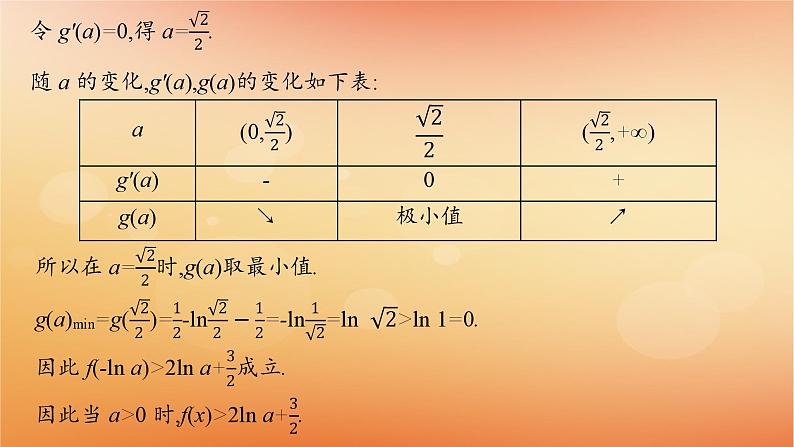
例1(2023新高考Ⅰ,19)已知函数f(x)=a(ex+a)-x.(1)讨论f(x)的单调性;(2)证明:当a>0时,f(x)>2ln a+ .
(1)解 f'(x)=aex-1,x∈R.①当a≤0时,f'(x)≤0对任意x∈R恒成立,所以f(x)在(-∞,+∞)内单调递减.②当a>0时,令f'(x)=0,得x=ln =-ln a.随x的变化,f'(x),f(x)的变化如下表:
所以函数f(x)的单调递增区间是(-ln a,+∞),单调递减区间是(-∞,-ln a).综上,当a≤0时,f(x)的单调递减区间是(-∞,+∞),无单调递增区间;当a>0时,f(x)的单调递增区间是(-ln a,+∞),单调递减区间是(-∞,-ln a).
[对点训练1](2024四川广安二模)已知函数f(x)=ex-ax-1.(1)若f(x)存在极值,求a的取值范围;(2)若a≤1,x∈(0,+∞),证明:f(x)>x-sin x.(1)解 由f(x)=ex-ax-1,x∈R,得f'(x)=ex-a,当a≤0时,f'(x)>0,则f(x)单调递增,f(x)不存在极值;当a>0时,令f'(x)=0,则x=ln a,当x0,即f(x)在(ln a,+∞)内单调递增.所以x=ln a是f(x)的极小值点,所以当a>0时,f(x)存在极值.综上所述,f(x)存在极值时,a的取值范围是(0,+∞).
(2)证明 欲证不等式f(x)>x-sin x在x∈(0,+∞)时恒成立,只需证明ex+sin x-(a+1)x-1>0在x∈(0,+∞)时恒成立.设g(x)=ex+sin x-(a+1)x-1,x∈(0,+∞),则g'(x)=ex+cs x-(a+1),令m(x)=g'(x)=ex+cs x-(a+1),x∈(0,+∞),则m'(x)=ex-sin x.当x∈(0,+∞)时,ex>1,-1≤-sin x≤1,所以m'(x)>0,所以m(x)即g'(x)在(0,+∞)内单调递增,所以g'(x)>g'(0)=1-a,因为a≤1,所以g'(0)=1-a≥0,故当x∈(0,+∞)时,g'(x)>0,所以g(x)在(0,+∞)内单调递增,所以g(x)>g(0)=0,即当a≤1,x∈(0,+∞)时,不等式f(x)>x-sin x恒成立.
考点二 分离函数法证明不等式
例2(2024安徽合肥模拟)已知函数f(x)=ax-ln x,a∈R.(1)若函数F(x)=f(x)-x2有两个极值点,求a的取值范围;
F(x)有两个极值点,所以方程-2x2+ax-1=0有两个不相等的正实根,当0x2时,F'(x)0,∴g'(x)在[0,+∞)内单调递增,∴g'(x)≥g'(0)=0,∴g(x)在[0,+∞)内单调递增,由g(x)为偶函数知,g(x)在(-∞,0]内单调递减,∴g(x)≥g(0)=-1.
考点三 放缩法证明不等式
当a≥0时,因为x>0,所以f'(x)>0恒成立,则y=f(x)在(0,+∞)内单调递增,且f(1)=0,所以f(x)恒大于或等于零不成立;当a0,当0
相关课件
这是一份2025届高考数学二轮总复习专题1函数与导数专题突破练5利用导数证明问题课件,共16页。
这是一份2025届高考数学二轮总复习专题1函数与导数专项突破1突破3利用导数研究函数的零点课件,共30页。
这是一份2025届高考数学二轮总复习专题1函数与导数专项突破1突破1利用导数求参数的值或范围课件,共35页。









