
所属成套资源:人教版数学六下PPT课件整册
数学六年级下册图形的认识与测量一等奖课件ppt
展开
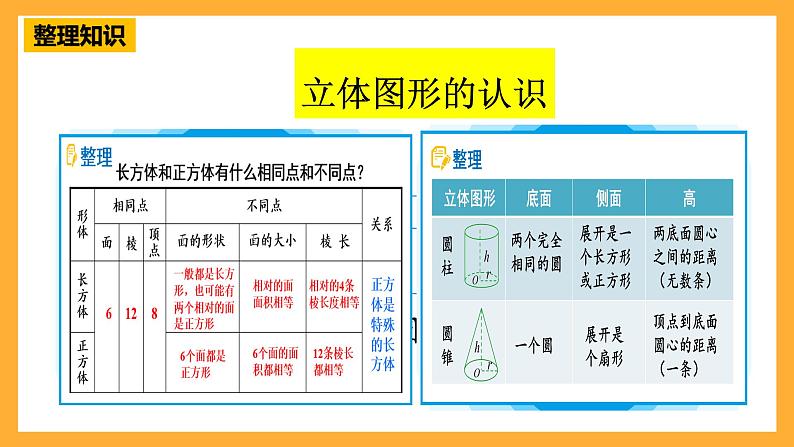
这是一份数学六年级下册图形的认识与测量一等奖课件ppt,共31页。PPT课件主要包含了立体图形的认识,不规则形状,规则形状,共同点,查漏补缺,方法二,S正方体6a2,体积不变,找联系等内容,欢迎下载使用。
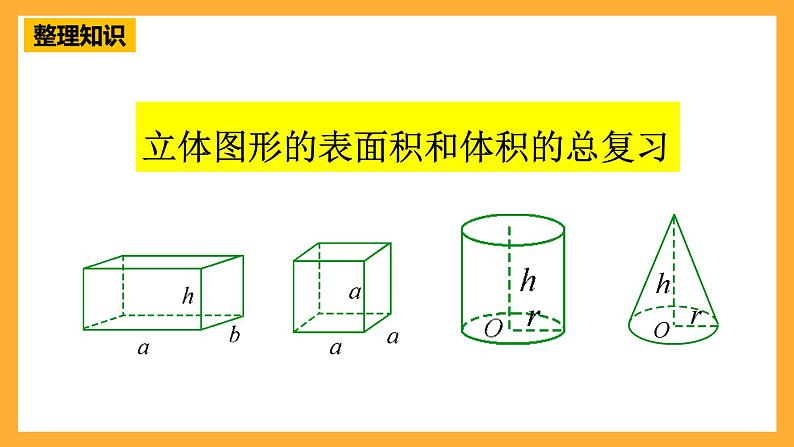
立体图形的表面积和体积的总复习
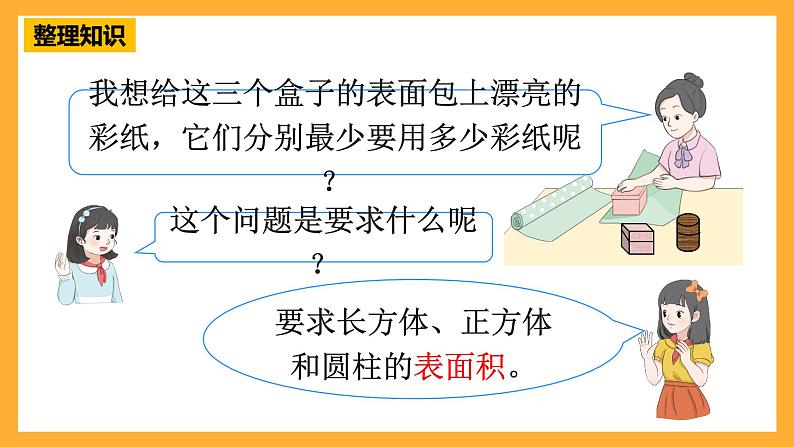
我想给这三个盒子的表面包上漂亮的彩纸,它们分别最少要用多少彩纸呢?
这个问题是要求什么呢?
要求长方体、正方体和圆柱的表面积。
这些立体图形的表面积指的是什么呢?
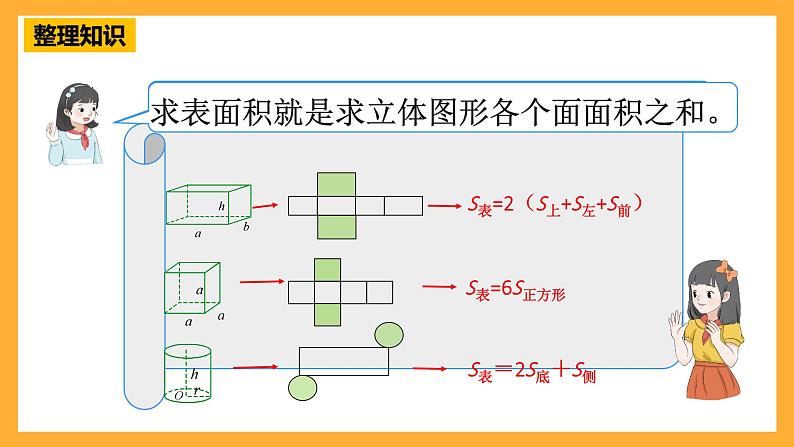
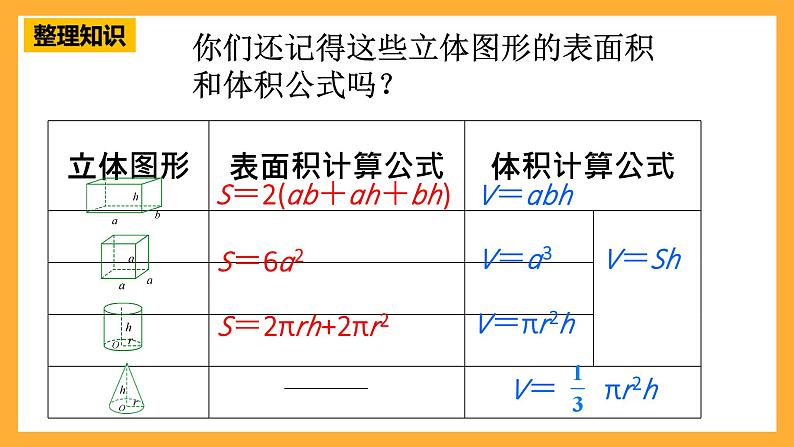
S表=2(S上+S左+S前)
求表面积就是求立体图形各个面面积之和。
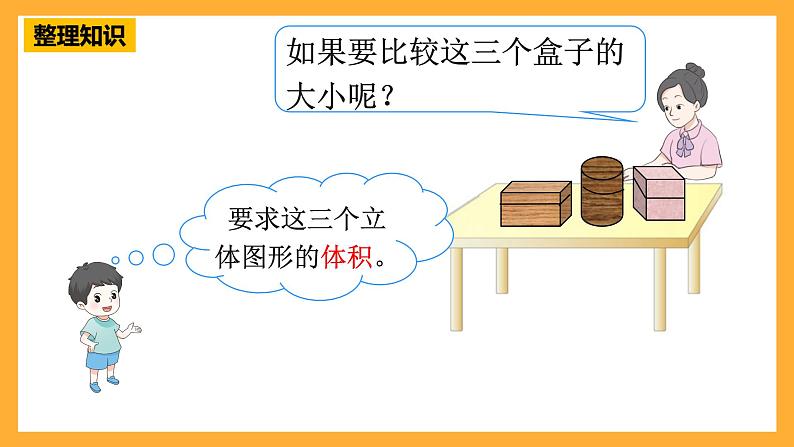
如果要比较这三个盒子的大小呢?
要求这三个立体图形的体积。
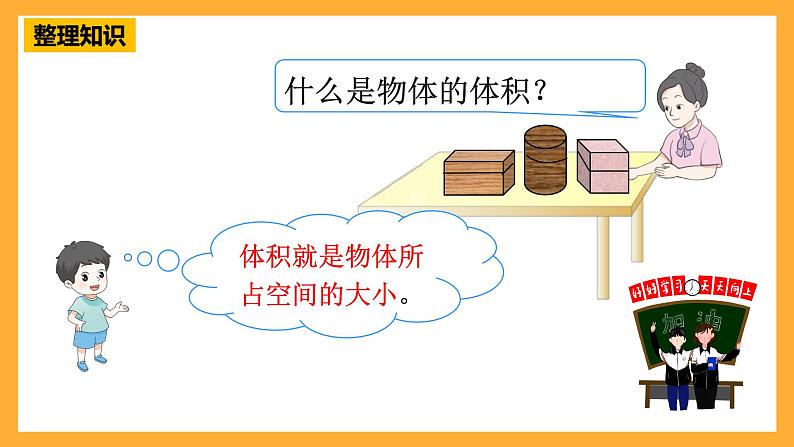
体积就是物体所占空间的大小。
S=2(ab+ah+bh)
S=2πrh+2πr2
你们还记得这些立体图形的表面积和体积公式吗?
你们还记得这些立体图形体积公式的推导过程吗?
V长方体=S底h=abh
可以把马铃薯看成一个规则的长方体或正方体形状,再测量相关数据计算出体积。
还可以用排水法,水面上升的那部分水的体积就是马铃薯的体积。
1. 把一个棱长为6cm的正方体切成棱长为2cm的小正方体,可以得到多少个小正方体?它们的表面积之和比原来大正方体的表面积增加了多少?
(教材第89页第10题)
方法一:V正方体=a3
大正方体的体积:6×6×6=216(cm3)
小正方体的体积:2×2×2=8(cm3)
小正方体的个数: 216÷8=27(个)
每条棱的小正方体个数:6÷2=3(个)
小正方体的总个数:3×3×3=27(个)
大正方体的表面积:6×6×6=216(cm2)
27个小正方体的表面积:2×2×6×27=648(cm2)
增加的面积:648 – 216=432(cm2)
答:可以得到27个小正方体,它们的表面积之和比原来大正方体的表面积增加了432cm2。
2. 把一个棱长为10cm的正方体铁块熔铸成一个底面直径是20cm的圆锥形铁块。这个圆锥形铁块的高约是多少?(得数保留一位小数。)
(教材第90页第11题)
答:这个圆锥形铁块的高约是9.6cm。
正方体的体积:103=1000(cm3)
圆锥的高:1000×3÷[3.14×(20÷2)2]
=3000÷314≈9.6(cm)
3.一个箱子下半部的形状是棱长为20 cm的正方体,上半部的形状是圆柱的一半。算出它的表面积和体积。
=628+314=942(cm2)
(教材第90页第13题)
正方体的5个面的面积和
3.14×20×20÷2
+3.14×(20÷2)2
=942+2000=2942(cm2)
=3140+8000=11140(cm3)
3.14×102×20÷2
4.*一个正方形的内部有一个四分之一圆(涂色部分)。已知正方形的面积是10cm2,涂色部分的面积是多少?
(教材第90页第15题)
圆的面积和正方形的面积有什么关系?
31.4÷4=7.85(cm2)
答:涂色部分的面积是7.85cm2。
3.14×r×r=3.14×10=31.4(cm2)
5.*用一根长24cm的铁丝围一个长方体(或正方体)框架。在这个长方体的表面糊一层纸,怎样围框架用纸最多?
已知棱长和,求表面积。
长、宽、高的和:24÷4=6(cm)
(教材第90页第16题)
4×1×4+1×1×2=18
(3×2+3×1+2×1)×2=22
(长、宽、高是整厘米数)
我发现当长方体棱长和一定时,长、宽、高相差越大,表面积就越小;长、宽、高相差越小,表面积就越大。
同学们,今天的数学课你们有哪些收获呢?
立体图形的表面积和体积
完成本课时的相关习题。
相关课件
这是一份人教版(2024)六年级下册图形的认识与测量获奖ppt课件,共28页。PPT课件主要包含了查漏补缺,立体图形的认识等内容,欢迎下载使用。
这是一份小学数学图形的认识与测量优秀课件ppt,共28页。PPT课件主要包含了平面图形的周长和面积,平面图形的周长,cm2,查漏补缺等内容,欢迎下载使用。
这是一份小学数学人教版六年级下册图形的认识与测量优秀课件ppt,共20页。PPT课件主要包含了课前热身,复习总览,课后作业,知识梳理,深化知识,拓展延伸,立体图形的认识,图形与几何,正方体,长方体等内容,欢迎下载使用。










