2023-2024学年重庆市鲁能巴蜀小学六年级（下）月考数学试卷（2）

这是一份2023-2024学年重庆市鲁能巴蜀小学六年级（下）月考数学试卷（2），共20页。试卷主要包含了克水，浓度就了变成25%，厘米等内容，欢迎下载使用。
1．（3分）已知●+●+●＝12，★+★+★+★+★＝25，则●×★＝（ ）
A．15B．20C．16D．30
2．（3分）下面四种说法中，正确的是（ ）
A．2时40分＝2.4时
B．假分数的倒数一定是真分数
C．一个钝角减去一个锐角后一定是锐角
D．长5cm、5cm和7cm的三根小棒一定可以围成等腰三角形
3．（3分）张老师等七位老师要一起外出参加活动，为了联络方便，要建立一个“通讯网”。若通知的方式是打电话，每个电话要1分，下面方案最节省时间的是（ ）
A． B．
C． D．
4．（3分）一个画家有14个棱长为1分米的正方体，他在地面上把它们摆成如图所示的几何体，然后他把露出的表面都涂上颜色，那么被涂上颜色的总面积为（ ）
A．42平方分米B．36平方分米
C．33平方分米D．27平方分米
5．（3分）在250克浓度为40%的盐水中只要加入（ ）克水，浓度就了变成25%．
A．100B．150C．350D．400
6．（3分）盒子里有黑白两种棋子，先放入一些白棋子，这样使得盒子中黑白棋子的比是2：5，然后又放入一些黑棋子，这样使得盒子中的黑白棋子的比是3：5．如果放入的黑棋子和白棋子的数量比是3：7，那么原来盒子中黑白棋子的数量之比是（ ）
A．6：5B．5：6C．4：3D．3：4
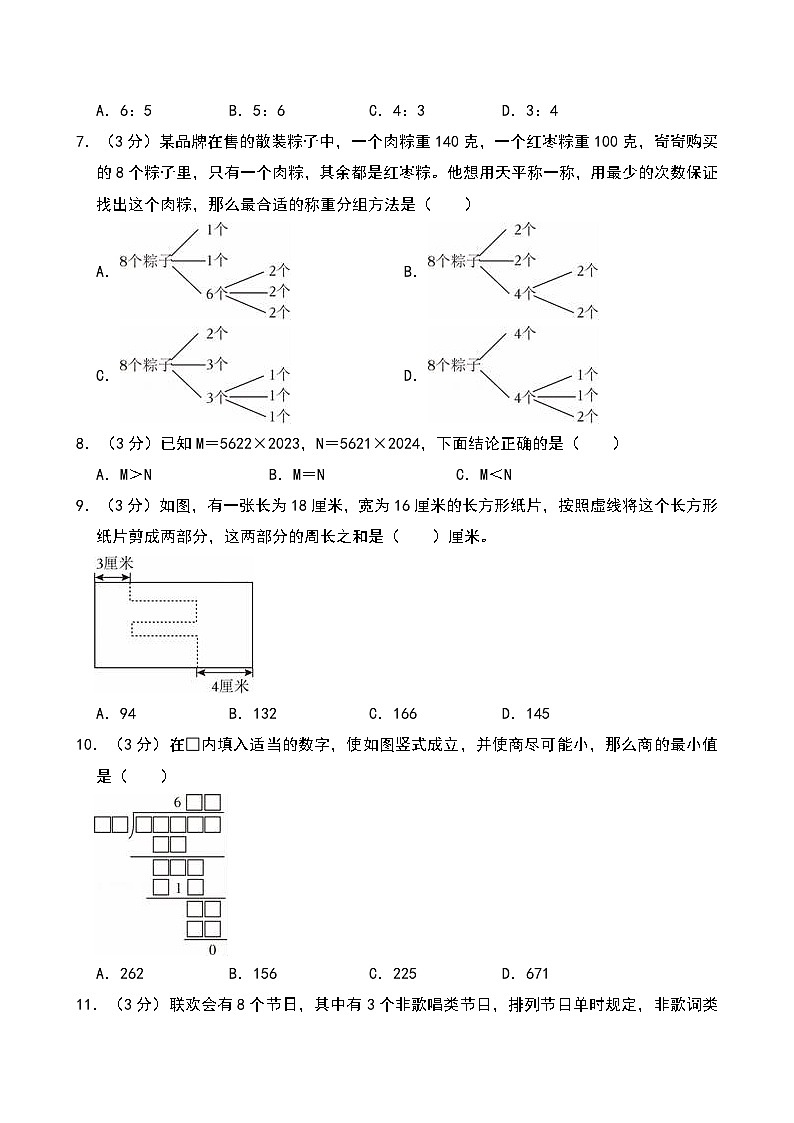
7．（3分）某品牌在售的散装粽子中，一个肉粽重140克，一个红枣粽重100克，奇奇购买的8个粽子里，只有一个肉粽，其余都是红枣粽。他想用天平称一称，用最少的次数保证找出这个肉粽，那么最合适的称重分组方法是（ ）
A． B．
C． D．
8．（3分）已知M＝5622×2023，N＝5621×2024，下面结论正确的是（ ）
A．M＞NB．M＝NC．M＜N
9．（3分）如图，有一张长为18厘米，宽为16厘米的长方形纸片，按照虚线将这个长方形纸片剪成两部分，这两部分的周长之和是（ ）厘米。
A．94B．132C．166D．145
10．（3分）在□内填入适当的数字，使如图竖式成立，并使商尽可能小，那么商的最小值是（ ）
A．262B．156C．225D．671
11．（3分）联欢会有8个节日，其中有3个非歌唱类节目，排列节目单时规定，非歌词类节目不相邻，而且第一个和最后一个节目都是歌唱类节目。则节目单可有（ ）种不同的排法。
A．1400B．2880C．960D．3250
12．（3分）几百年前，大数学家欧拉提出过一个猜想：至少n个n次方数加起来才能等于一个n次方数，几百年后两个数学家找到了一个反例，推翻了这个猜想，只需要4个5次方数加起来就能等于一个5次方数，当然也许还有其他反例，如果大家能找到也可以发表，从而青史留名，以275+845+1105+1335＝1445为反例推翻了欧拉猜想，那么问题来了。277+847+1107+1337（ ）
A．小于1447﹣1B．等于1447﹣1
C．等于1447D．等于1447+2
二、填空题（共12小题，每题2分，共24分）
13．（2分）数一数，如图中一共有 个正方形。
14．（2分）一筐苹果重60千克，第一天吃了它的，第二天吃了千克。还剩 千克。
15．（2分）给甲、乙、丙三位歌手投票，每位投票人可投给任意两名歌手，至少有 个人投票，才能保证其中至少有4个投票人的投票情况完全相同．
16．（2分）学校教学楼在花坛的北偏东60°方向的50米处，实验楼在教学楼的北偏西30°方向30米处，图书馆在实验楼的南偏西60°方向的50米处，那么，图书馆在花坛的 方向 米处。
17．（2分）某商场购进一批服装，每件进价为200元，由于换季滞销，商场决定将这批服装按标价的8折销售。若打折后每件服装仍能获利30%，则这批服装每件的标价为 元。
18．（2分）钟面上的时间是10：15，再经过t分钟，时针、分针第一次重合。则t为 。
19．（2分）已知某铁路桥长1600米，现有一列火车从桥上通过，测得火车从开始上桥到完全过桥共用90秒，整列火车完全在桥上的时间是70秒。则这列火车长 米。
20．（2分）仓库有一批货物，运走的货物与剩下的货物的质量比为3：8，如果又运走50吨，那么剩下的货物只有仓库原有货物的，仓库原有货物 吨。
21．（2分）如图所示，在半径为20的⊙O中，点C、点D是弧AB的三等分点，点E是直径AB的延长线上一点，连接CE、DE，则图中阴影部分的面积是 。
22．（2分）把所有正偶数从小到大排列，并按如下规律分组，（2），（4，6，8），（10，12，14，16，18），（20，22，24，26，28，30，32）……，若Am＝（i，j）表示正偶数M是第i组第j个数（从左往右数），若A8＝（2，3），则A2022＝ 。
23．（2分）小王、小李、小张三人做数学练习题，小王做的题数的一半等于小李的，等于小张的，而且小张比小李多做了20道，小李做了 道。
24．（2分）一辆自行车的前齿轮轮数是34个，后齿轮轮数是24个，车轮半径是33厘米。这辆自行车蹬一圈大约能走 厘米？（保留整数）
三、计算题（共1小题，每题4分，共16分）
25．（16分）计算题。
（1） （2）
（3） （4）
四、应用题（共4小题，每题6分，共24分）
26．（6分）一辆大货车与一辆小轿车同时从甲地开往乙地，小轿车到达乙地后立即返回，返回时速度提高25%，出发3小时后，小轿车与大货车第一次相遇，当大货车到达乙地时，小轿车刚好走到甲、乙两地的中点，则小轿车从甲到乙地花了多长时间？
27．（6分）做一批儿童玩具，甲组单独做10天完成，乙组单独做12天完成，丙组每天可生产64件，如果让甲、乙两组合做4天，则还有256件没完成，现在决定三个组合做这批玩具，需要多少天完成？
28．（6分）如图（1）是甲、乙两个完全相同的圆柱形水槽的轴截面示意图，在乙槽中放入一圆柱形实心铁块，两水槽在下侧位置连通（由连通阀门控制水泵、连过阀门处的水量忽略不计）。现将连通阀门打开。甲槽中的水匀速注入乙槽，甲、乙两个水槽中水的深度y（cm）与注水时间x（min）之间的关系如图（2）所示，则甲、乙两个水槽中水的深度相同时为多少cm？
29．（6分）一个各个数位上的数字均不为0的四位正整数，若千位上的数字与个位上的数字之和是百位上的数字与十位上的数字之和的2倍，则将这个四位数为“倍和数”，对于“倍和数”m，任意去掉一个数位上的数字，得到四个三位数，这四个三位数的和记为F（m）
（1）F（6312）＝ 。
（2）若“倍和数”m千位上的数字与个位上的数字之和为8，且能被7整除，求出所有满足条件的“倍和数”m的值。
参考答案与试题解析
一.选择题（共12小题，每题3分，共36分）
1．【分析】根据乘法的意义，3个●相加，用乘法表示为●×3，所以●×3＝12，用12÷3即可求出●；同理，5个★相加，用乘法表示为★×5＝25，用25÷5即可求出★，再把数据代入●×★即可求出结果。
【解答】解：12÷3＝4
25÷5＝5
4×5＝20
已知●+●+●＝12，★+★+★+★+★＝25，则●×★＝20。
故选：B。
【点评】本题考查了除法的意义。
2．【分析】低级单位时化高级单位分除进率60；
根据等于1的分数也是假分数，1的倒数还是1，即可判断；
令钝角为170°，锐角分别为70°，80°，85°，则其差分别为钝角，直角，锐角；
根据三角形的特征，任意两边之和大于第三边，任意两边之差小于第三边。据此判断。
【解答】解：A．2时40分＝2时，原题干表述错误；
B．假分数的倒数一定是真分数是错误的；
C．一个钝角减去一个锐角后一定是锐角是错误的；
D．长5cm、5cm和7cm的三根小棒一定可以围成等腰三角形，表述正确。
故选：D。
【点评】此题考查了三角形的分类、倒数的认识和三角形的特征等知识点。
3．【分析】每个老师通知另一个老师的需要1分钟，分别计算四个选项通知所用的时间，做出比较即可。
【解答】解：A．每一步都需要1分，共6步，需要6分钟。
B．1通知2需要1分钟，1通知3同时2通知5需要1分钟，1通知4同时2通知6同时3通知7需要1分钟，共需要3分钟。
C．1通知2需要1分钟，1通知3同时2通知5需要1分钟，1通知4和3通知6需要1分钟，4通知7需要1分钟，共需要4分钟。
D．1通知2需要1分钟，1通知3同时2通知4需要1分钟，2通知5同时3通知6需要1分钟，3通知7需要1分钟，共需要4分钟。
所以最节省时间的是B方案。
故选：B。
【点评】解决此题要明确：已通知的老师人数加上第一位老师是下一次要通知的老师人数。
4．【分析】可分层求出染色的表面是多少，然后再把各层染色的表面加起来．据此解答．
【解答】解：从下面数第一层露出的侧面是：
3×4＝12（个）
第二层露出的侧面是：
2×4＝8（个）
第三层露出的侧面是：
1×4＝4（个）
第一层的上面露出的面是：
3×3﹣4＝9﹣4＝5（个）
第二层的上面露出的面是：
2×2﹣1＝4﹣1＝3（个）
第三层上面露出的面是：1个．
12+8+4+5+3+1＝33（个）
1×1×33＝33（平方分米）
答：被涂上颜色的总面积为33平方分米．
故选：C。
【点评】本题的关键是每层上面露出的面是下面组成的面减去上面组成的面的个数．
5．【分析】根据因盐的重量不变，先求出盐的重量，再求出浓度25%时盐水的重量，减去250即可．据此解答．
【解答】解：250×40%÷25%﹣250，
＝250×0.4÷0.25﹣250，
＝400﹣250，
＝150（克）；
答：要加入150克水．
故选：B．
【点评】本题的关键是盐的重量不变，然后根据含盐率公式解答．
6．【分析】设原来盒子中黑棋子有x个，白棋子有y个，第一次放入白棋子，黑棋子不变，所以这时白棋子有个，放入了个白棋子；同理，第二次放入黑棋子，白棋子不变，所以这时黑棋子有×个，放入了×﹣x个白棋子；然后根据放入的黑棋子和白棋子的数量比是3：7，列比例式解答即可．
【解答】解：设原来盒子中黑棋子有x个，白棋子有y个，
（×﹣x）：（）＝3：7
整理得：3y＝4x
x：y＝3：4
答：原来盒子中黑白棋子的数量之比是3：4．
故选：D．
【点评】本题属于比较复杂的比例的应用，关键理解每次变化中谁是不变的量，用不变的量表示变化的量，这是解答的难点．
7．【分析】找次品时，第一次要尽量平均分成三个组，据此解答即可。
【解答】解：8÷3＝2⋯⋯2，所以3个组分成：3个，3个，2个；3÷3＝1，所以3个组分成1个，1个，1个，比较合适。
故选：C。
【点评】本题考查找次品，解答本题的关键是掌握找次品的计算方法。
8．【分析】如果一个因数乘或除以一个不为0的数，另一个因数不变，那么，它们的积也乘或除以同一个不为0的数，如果一个因数乘或除以一个不为0的数，另一个因数除以或乘同一个不为0的数，那么，它们的积不变。
【解答】解：M＝5622×2023＝11373306
N＝5621×2024＝11376904
M＜N
故选：C。
【点评】本题考查的主要内容是积的变化规律问题。
9．【分析】由图中数据可以知道虚线部分横着的每条线段长为18﹣3﹣4＝11（厘米），竖着的几条线段之和是16厘米，用虚线线段之和的2倍加上原来长方形的周长就可以求出答案。
【解答】解：18﹣3﹣4＝11（厘米）
11×3×2+16×2+（18+16）×2
＝66+32+68
＝166（厘米）
答：这两部分的周长之和是166厘米。
故选：C。
【点评】此题的关键是分析增加的虚线部分长度要算2次。
10．【分析】根据除法竖式商的百位6乘除数等于两位数，而商的十位乘除数等于三位数可知：商的十位大于商的百位。所以商的十位最小为7，个位最小为1，所以商的最小可能值是671。然后验证当商是671时是否满足题意即可。
【解答】解：根据除法竖式商的百位6乘除数等于两位数，而商的十位乘除数等于三位数可知：商的十位大于商的百位。
所以商的十位最小为7，个位最小为1，所以商的最小可能值是671；
当商是671时，由“除数×6≤99”和“除数×7≥110“得除数是16。
即16×671＝10736，即被除数是10736。
所以10736÷16＝671，满足题意且商最小。
答：商的最小值为671。
故选：D。
【点评】本题考查了除法的竖式数字谜的解题方法，知道从哪里入手填数字是解题的关键，能激起学生学习的兴趣，是个好题。
11．【分析】
如图所示，长方形代表3个非歌唱类节目，圆代表歌唱类节目，排节目时分两步完成，第一步：先排5个歌唱类节目，遵守乘法原理，有5×4×3×2×1种方法，第二步：因为第一个和最后一个节目是歌唱类节目，只能在5个歌唱类节目中间形成的4个空中任选三个，填三个非歌唱类节目遵守乘法原理有4×3×2种方法；总共的排法同样遵守乘法原理。
【解答】解：（5×4×3×2×1）×（4×3×2）＝120×24＝2880（种）
答：节目单有2880种不同的排法。
故选：B。
【点评】本题考查了乘法原理：做一件事，完成它需要分成n个步骤，做第一步有m1种不同的方法，做第二步有m2种不同的方法……，做第n步有mn种不同的方法，那么完成这件事共有N＝m1×m2×m3×……×mn种不同的方法。
12．【分析】依据题意可知，277+847+1107+1337＝272×275+842×845+1102×1105+1332×1335，已知275+845+1105+1335＝1445，由此解答本题。
【解答】解：277+847+1107+1337＝272×275+842×845+1102×1105+1332×1335，
已知275+845+1105+1335＝1445，1332×（275+845+1105+1335）＝1332×1445，
则277+847+1107+1337＝272×275+842×845+1102×1105+1332×1335＜1332×（275+845+1105+1335），即277+847+1107+1337＜1332×1445，
1332×1445＜1442×1445﹣1＝1447﹣1，所以277+847+1107+1337＜1447﹣1，
故选：A。
【点评】本题考查的是有理数的乘方的应用。
二、填空题（共12小题，每题2分，共24分）
13．【分析】可以采用列举法，依次列出不同边长的正方形有几个，然后加起来即可。
【解答】解：假设每个小正方形的边长为1，边长为1的有12个，边长为2的有6个，边长为3的有2个。
12+6+2＝20（个）
答：一共有20个正方形。
故答案为：20。
【点评】熟练掌握对正方形的认识是解题关键。
14．【分析】用这筐苹果的质量乘，即可计算出第一天吃的质量，再用这筐苹果的质量减去第一天吃的质量，再减去第二天吃的质量，即可计算出还剩多少千克。
【解答】解：60×＝15（千克）
60﹣15﹣
＝45﹣
＝44（千克）
答：还剩44千克。
故答案为：44。
【点评】本题解题的关键是根据分数乘法的意义与分数减法的意义，列式计算。
15．【分析】从3名歌手选出2名，共有：2+1＝3种选法，要保证至少4人投两人相同的票，至少需：（3×3+1）人投票；据此解答即可．
【解答】解：从3名歌手选出2名，共有：2+1＝3种选法，要保证至少4人投两人相同的票，至少需：
3×3+1＝10（人），
答：至少有10人投票，能保证其中至少有4个投票人的投票情况完全相同．
故答案为：10．
【点评】此题属于较复杂的抽屉原理习题，解答此题的关键是认真分析题意，弄清题目的意思，进而通过分析、得出结论．
16．【分析】根据题意，可根据上北下南，左西右东的方法绘制示意图进行理解，在图中可将教学楼与实验楼、实验楼与图书馆、图书馆与花坛、花坛与教学楼相连接，连接后可知：花坛、教学楼、实验楼、图书馆围成了一个长为50米，宽为30米的长方形，根据长方形的性质可知图书馆与花坛的距离为30米，阴影图书馆、花坛、教学楼围成了一个直角，教学楼再花坛的北偏东60度上，所以图书馆就在花坛北偏西30°方向上。
【解答】解：作图如下：
答：图书馆在花坛的北偏西30°方向的30米处。
故答案为：北偏西30°，30。
【点评】解答此题的关键是确定观察的中心点，然后再根据上北下南左西右东的方法进行确定方向和位置即可。
17．【分析】利用进价乘30%求出获利的钱数，再利用进价加上获利的钱数除以折扣就是标价。
【解答】解：200×30%＝60（元）
（200+60）÷80%
＝260÷0.8
＝325（元）
答：这批服装每件的标价为325元。
故答案为：325。
【点评】本题考查了原价、折扣及现价之间的关系。
18．【分析】分针每小时转360°，时针每小时转30°，则分针每分钟转360°÷60＝6°，时针每分钟转30°÷60＝0.5°，根据钟面上的时间是10：15，再经过t分钟，时针、分针第一次重合，可看作追及问题，列出关于t的一元一次方程。由此解答。
【解答】解：6t﹣0.5t＝217.5
5.5t＝217.5
t＝
答：t为。
故答案为：。
【点评】此题考查钟表问题的应用。
19．【分析】火车从开始上桥到完全过桥行驶的路程＝某铁路桥长+这列火车的长，整列火车完全在桥上行驶的路程＝某铁路桥长﹣这列火车的长，设这列火车的长为x米，利用“速度＝路程÷时间”，结合火车的速度不变，即可得出关于x的一元一次方程，此题得解。
【解答】解：设这列火车的长为x米。
＝
70（1600+x）＝90（1600﹣x）
7（1600+x）＝9（1600﹣x）
11200+7x＝14400﹣9x
7x+9x＝14400﹣11200
16x＝3200
x＝200
答：这列火车长200米。
故答案为：200。
【点评】本题考查了由实际问题抽象出一元一次方程，找准等量关系，正确列出一元一次方程是解题的关键。
20．【分析】将这批货物总吨数看作单位“1”，原来剩下货物总吨数的，又运走50吨后剩下货物总吨数的，则又运走的50吨占原有货物总吨数的（），据此解答。
【解答】解：50÷（）
＝50÷
＝275（吨）
答：仓库原有货物275吨。
故答案为：275。
【点评】本题考查了利用比的知识及整数与分数除减混合运算解决问题，分析出又运走的50吨占原有货物总吨数的几分之几是关键。
21．【分析】点C、点D是弧AB的三等分点，则CD∥AE，所以三角形CDE的面积等于三角形CDO的面积，所以图中阴影部分的面积就等于扇形COD的面积；又因为点C、点D是弧AB的三等分点，所以∠COD＝180÷3＝60（度），即图中阴影部分的面积等于圆面积的；然后进一步解答即可。
【解答】解：∠COD＝180÷3＝60（度）
3.14×202×
＝3.14×400×
＝
答：图中阴影部分的面积是。
故答案为：。
【点评】解答本题关键得到三角形CDE的面积等于三角形CDO的面积。
22．【分析】依据题意，2022是这组数的第（2022÷2）个数，设2022在第n组，1+3+5+7+……+2n﹣1＝，找出符合要求的n，然后计算第组一个数是多少，再计算2022是第n组的第几个数。
【解答】解：2022÷2＝1011
设2022在第n组，1+3+5+7+……+2n﹣1＝＝n2
当n＝31时，n2＝961，
当n＝32时，n2＝1024，所以第1011个数在第32组，
第32组第一个数是：961×2+2＝1924
则2022是（2022﹣1924）÷2+1
＝49+1
＝50（个）
所以A2022＝（32，50）。
故答案为：（32，50）。
【点评】通过观察，分析、归纳发现其中的规律，并应用发现的规律解决问题是应该具备的基本能力。
23．【分析】根据题意，小王做的题数的一半等于小李的，小王做的题数的一半等于小张的，所以小王做的题数：小李做的题数：小张做的题数＝2：5：7，小张比小李多做了20道，据此求出20÷（7﹣5）×5＝50（道），据此解答。
【解答】解：因为小王做的题数的一半等于小李的，
所以小王做的题数与小李做的题数比是2：5，
因为小王做的题数的一半等于小张的，
所以小王做的题数与小张做的题数比是2：7，
所以小王做的题数：小李做的题数：小张做的题数＝2：5：7，
20÷（7﹣5）×5
＝20÷2×5
＝50（道）
答：小李做了50道。
故答案为：50。
【点评】本题考查了分数的除法应以，解决本题的关键是求出三人做的题数比。
24．【分析】自行车蹬一圈走的距离＝后轮外直径×π×（前齿轮数÷后齿轮数），据此公式来解答。
【解答】解：2×3.14×33×（34÷24）
＝207.24×
≈294（厘米）
答：蹬一圈大约能走294厘米。
故答案为：294。
【点评】理解并熟练运用公式：自行车瞪一圈走的距离＝后轮外直径×π×（前齿轮数÷后齿轮数）是解决此题的关键。
三、计算题（共1小题，每题4分，共16分）
25．【分析】（1）逆用乘法分配律即可简算；
（2）分子分母同时利用高斯求和公式即可简算；
（3）除了前两项之外的其他分数裂项相消即可简算；
（4）方程两边同时乘6，整理化简后方程两边同时加未知数，最后方程两边同时减6即可求解。
【解答】解：（1）
＝×13﹣3×+×
＝×（13﹣3+）
＝×（13+﹣3）
＝×（14﹣3）
＝×11
＝
（2）
＝
＝
＝
（3）
＝﹣+﹣+﹣+
＝1+﹣+++﹣﹣++﹣﹣++
＝1+﹣+++
＝+﹣+++
＝
（4）
2×（2x+1）﹣（5x﹣1）＝6
4x+2﹣5x+1＝6
3﹣x＝6
3﹣x+x＝6+x
3＝6+x
3﹣6＝6+x﹣6
﹣3＝x
x＝﹣3
【点评】本题考查了分数的四则混合运算以及根据等式的基本性质解方程。
四、应用题（共4小题，每题6分，共24分）
26．【分析】首先将甲乙两地之间的距离设为“1，设小轿车开始时的速度为x，通过分析大货车和小轿车的行程关系，逐步建立方程来求解小轿车的速度，进而求出小轿车从甲地到乙地的时间。
【解答】解：将甲乙两地之间的距离看成“1”，设小轿车开始时的速度为x。
由题意可知，小轿车返回速度为 （1+25%）x ＝x。
大货车到达乙地时，小轿车刚好返回走到甲乙两地的中点。
小轿车返回后走到甲乙两地中点用的时间为：
+÷x
＝+×
＝
所以大货车到达乙地用的时间为小时。
大货车的速度为1÷＝x。
小轿车到达乙地用时为，所以当小轿车到达乙地时，大货车走的路程为x×＝。
从小轿车返回到和大货车相遇，两车共同走的路程为1﹣＝，用时为3﹣。由此可以建立方程：
（x+x）×（3﹣）＝
x×（3﹣）＝
55x×（3﹣）＝8
165x﹣55＝8
165x＝63
x＝
所以小轿车从甲地到乙地花费时间为1÷＝（小时）。
答：小轿车从甲地到乙地花费小时。
【点评】解决本题关键是找清楚小轿车、货车它们的速度、路程和行驶时间之间的对应关系，再设出数据，利用它们之间的关系求解。
27．【分析】甲、乙两组合做4天，一共完成了（）×4＝，那么还剩下＝，利用对应量÷对应分率＝单位“1”，求出这批儿童玩具的总量，再根据已知条件求出甲的效率，乙的效率，用总数除以甲乙丙的效率之和，就是三个组合做这批玩具，需要多少天了。
【解答】解：（ ）×4＝
＝
256＝960（件）
960÷10＝96（件）
960÷12＝80（件）
960÷（96+80+64）＝4（天）
答：需要4天完成。
【点评】解答此题的关键是求出这批玩具一共有多少件，用总数除以甲乙丙的效率之和，就是三人合作需要多少时间。
28．【分析】依据题意结合图示可知，从4min到8min，乙槽中水面上升高度等于甲槽中水面下降高度，由此解答本题。
【解答】解：（29﹣14）÷3
＝15÷3
＝5（厘米）
29﹣5×2
＝29﹣10
＝19（厘米）
答：甲、乙两个水槽中水的深度相同时为19厘米。
【点评】解决本题的关键是读懂图示，找出题中数量关系。
29．【分析】（1）根据题意直接计算，即可解答；
（2）设m的千位数字为a，百位数字为b，得出m＝（1≤a≤7，1≤b≤3且a、b为整数），进而得出F（m）＝297a+99b+108。再根据＝7×（4a+b+2）+2b﹣a﹣1能被7整除，得出2b＝a+1，即可求出答案。据此解答。
【解答】解：（1）根据题意可得：
F（6312）
＝631+632+612+312
＝2187
答：F（6312）＝2187。
（2）设“倍和数”m的千位数字为a，百位数字为b。因为“倍和数”m千位上的数字与个位上的数字之和为8，
所以m的个位数字为（8﹣a）又因为千位上的数字与个位上的数字之和是百位上的数字与十位上的数字之和的2倍，
所以百位上的数字与十位上的数字之和为8÷2＝4，
所以m的十位数字为（4﹣b）。
即m＝（1≤a≤7，1≤b≤3且a、b为整数）。
所以F（m）＝+++
＝100a+10b+（4﹣b）+100a+10b+（8﹣a）+100a+10（4﹣b）+（8﹣a）+100b+10（4﹣b）+（8﹣a）
＝100a+10b+4﹣b+100a+10b+8﹣a+100a+40﹣10b+8﹣a+100b+40﹣10b+8﹣a
＝297a+99b+108
所以
＝
＝
＝
＝27a+9b+13
＝7×（4a+b+2）﹣a+2b﹣1
＝7×（4a+b+2）+2b﹣a﹣1
因为能被7整除，
所以7×（4a+b+2）+2b﹣a﹣1能被7整除，
即2b﹣a﹣1能被7整除。
因为1≤a≤7，1≤b≤3且a、b均为整数，
所以﹣6≤2b﹣a﹣1≤4即2b﹣a﹣1﹣0，
所以2b＝a+1
根据1≤a≤7，1≤b≤3且a、b均为整数可得：
a＝1，b＝1或a＝3，b＝2或a＝5，b＝3。
即m＝1137或3225或5313。
答：所有满足条件的“倍和数”m的值为1137或3225或5313。
故答案为：2187。
【点评】此题主要考查了定义新运算的应用、数的整除问题的应用以及位值原理的应用。