2024-2025学年北京市高二上册期中考练习数学检测试题（含解析）

这是一份2024-2025学年北京市高二上册期中考练习数学检测试题（含解析），共35页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
1．空间直角坐标系中，，则（ ）
A．B．C．D．
2．已知直线m，n，l，平面，下列正确的是（ ）
A．若，则与异面B．若，则
C．若，则D．若，则
3．在四面体中，点是AB靠近的三等分点，记，则（ ）
A．B．
C．D．
4．若圆锥的侧面积等于和它等高等底的圆柱的侧面积时，圆锥轴截面顶角的度数为（ ）
A．B．C．D．
5．已知直线m，n，平面，那么“”是“”的（ ）
A．充分必要条件B．必要不充分条件
C．充分不必要条件D．既不充分也不必要条件
6．在空间直角坐标系中，直线的方向向量，点在直线上，点到直线的距离是（ ）
A．B．C．D．
7．一个正棱锥，其侧棱长是底面边长的，这个正棱锥可能是（ ）
A．正三棱锥B．正四棱锥C．正五棱锥D．正六棱锥
8．正三棱锥中，为棱PA的中点，点M，N分别在棱PB，PC上，三角形周长的最小值为（ ）
A．B．C．D．
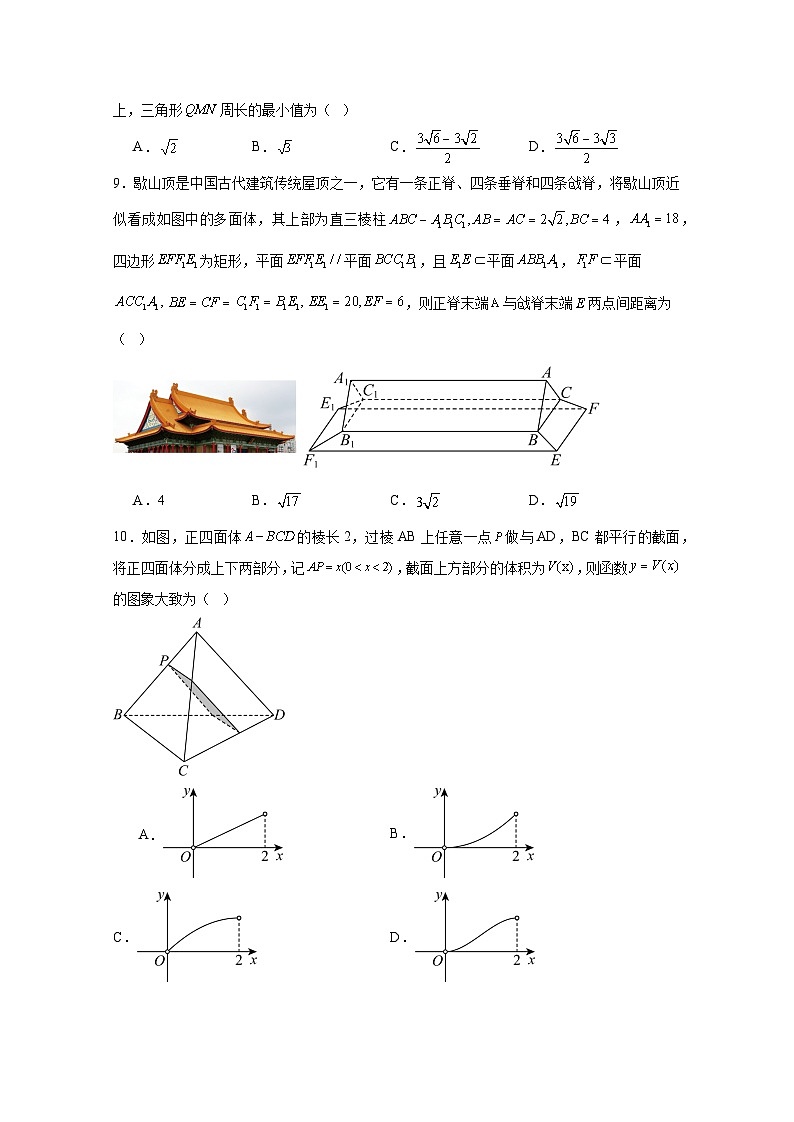
9．歇山顶是中国古代建筑传统屋顶之一，它有一条正脊、四条垂脊和四条戗脊，将歇山顶近似看成如图中的多面体，其上部为直三棱柱，，四边形为矩形，平面平面，且平面，平面，则正脊末端与戗脊末端两点间距离为（ ）

A．4B．C．D．
10．如图，正四面体的棱长2，过棱AB上任意一点做与AD，BC都平行的截面，将正四面体分成上下两部分，记，截面上方部分的体积为，则函数的图象大致为（ ）

B．
C． D．
二、填空题
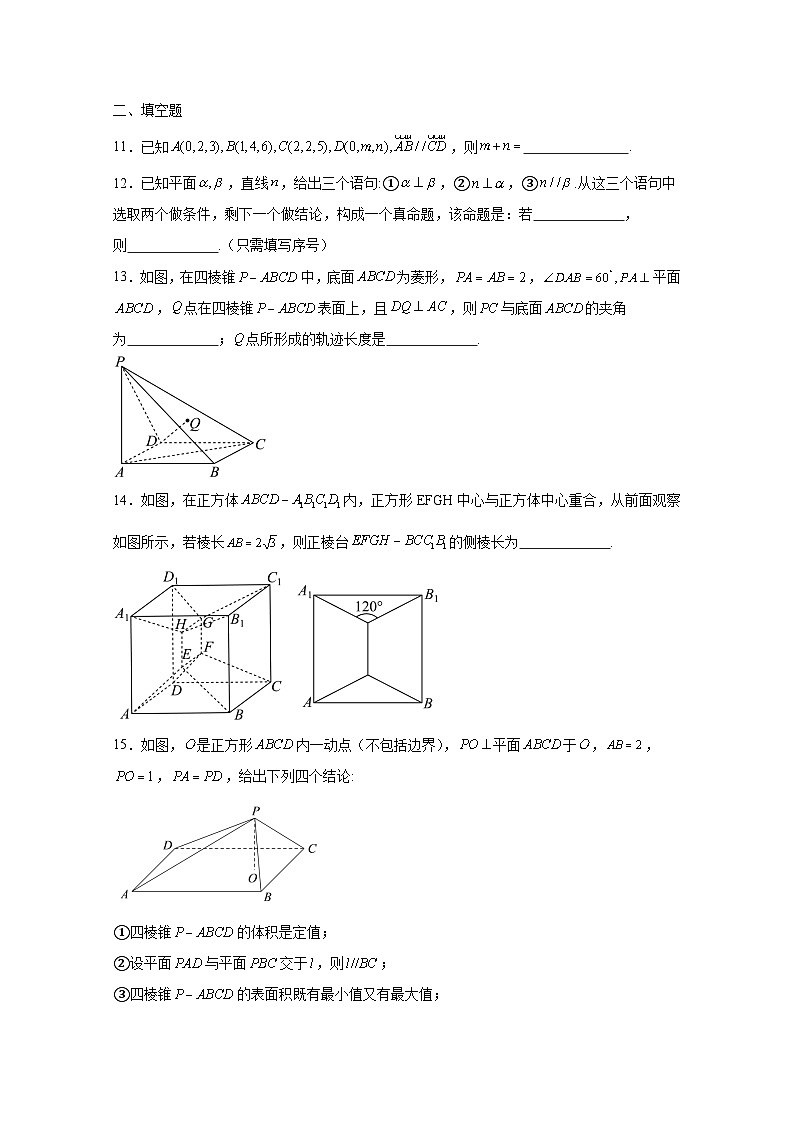
11．已知，则 .
12．已知平面，直线，给出三个语句:①，②，③.从这三个语句中选取两个做条件，剩下一个做结论，构成一个真命题，该命题是：若 ，则 .（只需填写序号）
13．如图，在四棱锥中，底面为菱形，，平面，点在四棱锥表面上，且，则与底面的夹角为 ；点所形成的轨迹长度是 .
14．如图，在正方体内，正方形EFGH中心与正方体中心重合，从前面观察如图所示，若棱长，则正棱台的侧棱长为 .
15．如图，是正方形内一动点（不包括边界），平面于，，，，给出下列四个结论:
①四棱锥的体积是定值；
②设平面与平面交于，则；
③四棱锥的表面积既有最小值又有最大值；
④存在点，使得四棱锥的四个侧面两两垂直.
其中所有正确结论的序号是 .
三、解答题
16．已知空间四点.
(1)求和的值;
(2)若点在平面ABC内，请直接写出的值.
17．如图，在直四棱柱中，底面为梯形，，其中是的中点，是的中点.
(1)求证:平面;
(2)求平面与平面所成角的余弦值.
18．如图，四棱锥P-ABCD中，平面.

(1)若，求证：平面平面PCD；
(2)若AD=DC，PB中点为，试问在棱CD上是否存在点，使，若存在，指出点位置，若不存在说明理由；
(3)若与平面PBC成角大小，求DC边长.
四、单选题
19．如图，在直三棱柱中，，则直线与直线所成的角为（ ）
A．B．C．D．
20．如图，正方体的棱长为，其中分别是棱的中点，则到平面的距离是（ ）

A．B．C．D．
21．如图1，在矩形中，，点在AB边上，且.如图2，将沿直线DE向上折起至位置，连结.记二面角的大小为，当时，下面四个结论中错误的是（ ）
A．存在某个位置，使
B．存在某个位置，使平面平面
C．存在某个位置，直线与平面所成角为
D．存在某个位置，使平面与平面的交线与平面DEC平行
22．光导纤维作为光的传输工具，在现代通讯中有着及其重要的作用，光纤由内部纤芯和外部包层组成（如图1），在一定的条件下，光在纤芯中传输，传输原理是“光的全反射”，即“入射角等于反射角”（如图2），在图3中近似的展示了一束光线在一段较长的圆柱形光纤中的传输路径，其中圆面是与光纤轴垂直的纤芯截面，若与圆所在平面成角的大小为，则光线路径在垂直于光纤轴的截面上的投影可能（ ）
B． C． D．
五、填空题
23．直二面角，则 ;三棱锥外接球的体积是 .
24．已知正方体的棱长为为侧面内一动点（包括边界），为棱上一动点（包括端点），则的最小值是 .
25．如图，某一个自行车停放时，车体由尺寸相同的前后轮和脚撑来支撑，前后轮的轴中心分别为，，与地面接触点分别为，，脚撑一端固定在后轮轴中心处，另一端与地面接触于点，若，两点间距离为厘米，车轮外径（直径）为厘米，脚撑长度等于车轮半径，，则后车轮所在平面与地面的夹角（即二面角）的余弦值为 .
26．将半径为1的半圆弧等分，从半径的一个端点出发依次连接各个分点至半径的另一个端点，得到折线，将折线绕半径MN所在直线旋转，得到旋转体（时，如图所示），设所得旋转体的表面积为，给出下列四个结论：
①；
②；
③最大值为；
④.
其中所有正确结论的序号是 .
27．已知正方体的棱长分别为中点，从开始沿射线DF运动，做平面，垂足为，给出下列四个结论：
①平面与平面夹角先增大后减小;
②B1N最大值为4，并且先增大后减小;
③存在N使得；
④存在唯一的使得.
其中所有正确结论的序号是 .
28．蜜蜂分泌蜂蜡筑巢，蜂巢由许多中空的柱状体连接而成，其中柱状体的一端为正六边形开口，另一端由三个全等的菱形拼成类似锥形的底部（如图1），蜜蜂这样筑巢能够使得蜂巢空间不变的条件下，所用蜂蜡最少，为了揭开蜜蜂筑巢的数学秘密，研学小组利用正六棱柱去研究中空的柱状体.设正六棱柱底面边长为，高为定值（大于底面边长），底面中心分别为（如图2），现将延长至，平面PFB，，分别与棱交于，，，得到中空的柱状体（如图3）.
（1）比大小：所得中空的柱状体的体积 原正六棱柱体积；（填“>”，“