

2024-2025学年贵州省毕节市金沙县高一上册期末考试数学检测试题(含解析)
展开
这是一份2024-2025学年贵州省毕节市金沙县高一上册期末考试数学检测试题(含解析),共17页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
一、单选题(本大题共8道小题,共40分,在每小题列出的选项中,选出符合题目的一项)
1. 设集合,则( )
A. B. C. D.
2. 已知命题:是素数,则为( )
A. 不素数B. 不是素数
C. 不是素数D. 不是素数
3. 以下对数式中,与指数式等价的是( )
A. B. C. D.
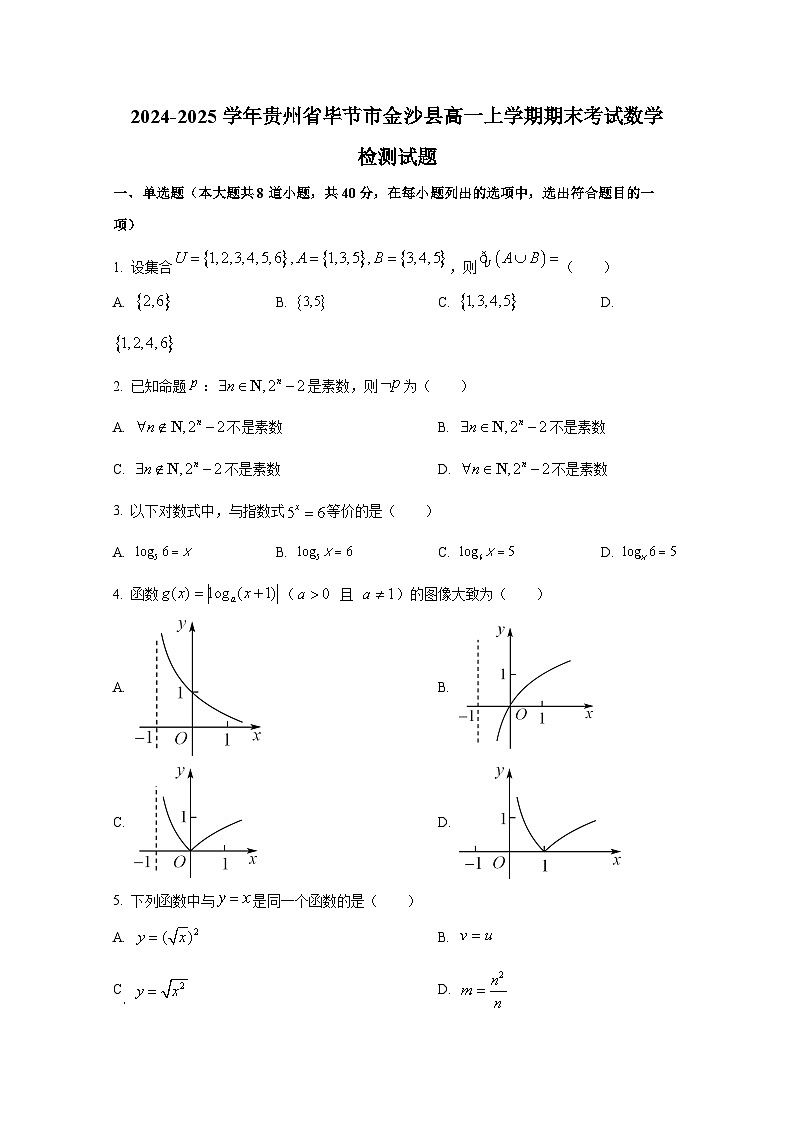
4. 函数( 且 )的图像大致为( )
A. B.
C. D.
5. 下列函数中与是同一个函数的是( )
A. B.
C D.
6. ( )
A. B. C. D.
7. 已知弧长为cm弧所对的圆心角为,则这条弧所在的扇形面积为( )cm2.
A. B. C. D.
8. 已知函数,满足对任意,都有成立,则的取值范围是( )
A. B. C. D.
二、多选题(本大题共四个小题,共20分,每小题有多项符合题目要求)
9. 判断下列每组对象,能组成一个集合的是( )
A. 某校高一年级成绩优秀的学生
B. 直角坐标系中横、纵坐标相等的点
C. 不小于3的自然数
D. 2022年第24届冬季奥运会金牌获得者
10. 下列命题正确的是( )
A. 若集合有个元素,则真子集的个数为
B. 函数的零点可以用二分法求得
C. 函数零点为
D. 函数的最小值为
11. 下列结论中,正确的是( )
A. 幂函数的图象都通过点
B. 互为反函数的两个函数的图象关于直线对称
C. 函数恒过定点
D. 函数在整个定义域内是单调递减的
12. 已知函数,则( )
A. 的定义域为B. 的图象关于轴对称
C. 的值域为D. 是减函数
三、填空题(本大题共4个小题,共20分)
13. 已知,则____________________________.
14. 已知奇函数,当时,,则__________.
15. “”是“”的_________________.(填“充分不必要条件”、“充要条件”、“必要不充分条件”、“既不充分也不必要条件”)
16. 若命题“”是假命题,则a的取值范围是_______.
四、解答题(本大题共6小题,共70分.解答过程应写出文字说明,证明过程或演算步骤)
17. 计算:
(1)+;
(2).
18. 已知集合.
(1)当时,求;
(2)若,求的取值范围.
19. 已知,α是第三象限角,求:
(1)的值;
(2)的值.
20. 已知函数的图象经过点,其中,且.
(1)求a的值;
(2)求函数的值域.
21. 已知函数,其中且.
(1)判断的奇偶性,并说明理由;
(2)若,求使成立的x的集合.
22. 某便民超市经销一种小袋装地方特色桃酥食品,每袋桃酥的成本为6元,预计当一袋桃酥的售价为元时,一年的销售量为万袋,并且全年该桃酥食品共需支付万元的管理费. 一年的利润一年的销售量售价(一年销售桃酥的成本一年的管理费).(单位:万元)
(1)求该超市一年的利润(万元)与每袋桃酥食品的售价的函数关系式;
(2)当每袋桃酥的售价为多少元时,该超市一年的利润最大,并求出的最大值.
2024-2025学年贵州省毕节市金沙县高一上学期期末考试数学
检测试题
一、单选题(本大题共8道小题,共40分,在每小题列出的选项中,选出符合题目的一项)
1. 设集合,则( )
A. B. C. D.
【正确答案】A
【分析】先求,再求补集可得答案.
【详解】集合,
则.
故选:A.
2. 已知命题:是素数,则为( )
A. 不是素数B. 不是素数
C. 不是素数D. 不是素数
【正确答案】D
【分析】根据存在量词命题的否定为全称量词命题即可得解.
【详解】因为存在量词命题的否定为全称量词命题,
所以为不是素数.
故选:D.
3. 以下对数式中,与指数式等价的是( )
A. B. C. D.
【正确答案】A
【分析】
根据指数式和对数式的关系即可得出.
【详解】根据指数式和对数式的关系,等价于.
故选:A.
4. 函数( 且 )的图像大致为( )
A. B.
C. D.
【正确答案】C
【分析】由函数图像过的定点和函数的值域可判断正确选项.
【详解】,函数定义域,
有,函数图像过原点,AD选项不符合,,B选项不符合.
故选:C.
5. 下列函数中与是同一个函数的是( )
A. B.
C. D.
【正确答案】B
【分析】根据函数相等的定义是:定义域相同且对应关系相同,逐个分析可得答案.
【详解】对于A,的定义域为,与的定义域为不同,故A不正确;
对于B,与是同一函数,故B正确;
对于C,与的对应关系不同,故C不正确;
对于D,与的定义域不同,故D不正确.
故选:B
6. ( )
A. B. C. D.
【正确答案】C
【分析】由诱导公式可得答案.
【详解】
.
故选:C
7. 已知弧长为cm的弧所对的圆心角为,则这条弧所在的扇形面积为( )cm2.
A. B. C. D.
【正确答案】C
【分析】根据弧长计算出半径,再利用面积公式得到答案.
【详解】弧长为cm的弧所对的圆心角为,则
故选
本题考查了扇形的面积,求出半径是解题的关键.
8. 已知函数,满足对任意,都有成立,则的取值范围是( )
A. B. C. D.
【正确答案】A
【分析】由对任意,可知, 为减函数,再列出不等式可求得a的取值范围.
【详解】由题意,函数对任意的都有成立,
即函数为上的减函数,
可得解得,
故选:A.
二、多选题(本大题共四个小题,共20分,每小题有多项符合题目要求)
9. 判断下列每组对象,能组成一个集合的是( )
A. 某校高一年级成绩优秀的学生
B. 直角坐标系中横、纵坐标相等的点
C. 不小于3的自然数
D. 2022年第24届冬季奥运会金牌获得者
【正确答案】BCD
【分析】判断是否满足集合三要素中的确定性,得到答案.
【详解】A中“成绩优秀”没有明确的标准,所以不能组成一个集合;
B、C、D中的对象都满足确定性,所以能组成集合.
故选:BCD
10. 下列命题正确是( )
A. 若集合有个元素,则的真子集的个数为
B. 函数的零点可以用二分法求得
C. 函数的零点为
D. 函数的最小值为
【正确答案】AD
【分析】根据集合真子集个数得公式即可判断A;根据二分法适用的条件即可判断B;根据零点的定义即可判断C;利用基本不等式即可判断D.
【详解】对于A,由题意真子集的个数为,故A正确;
对于B,,
且零点的两侧同号,
所以函数的零点不可以用二分法求得,故B错误;
对于C,令,得或,
所以函数的零点为,故C错误;
对于D,,
则,
当且仅当,即时,等号成立,
所以函数的最小值为,故D正确.
故选:AD.
11. 下列结论中,正确的是( )
A. 幂函数的图象都通过点
B. 互为反函数的两个函数的图象关于直线对称
C. 函数恒过定点
D. 函数在整个定义域内是单调递减的
【正确答案】BC
【分析】根据幂函数的性质即可判断A;根据反函数的定义即可判断B;根据指数函数的定值即可判断C;根据反比例函数的单调性即可判断D.
【详解】对于A,幂函数不过,故A错误;
对于B,互为反函数的两个函数的图象关于直线对称,故B正确;
对于C,令,则,
所以函数恒过定点,故C正确;
对于D,函数的单调减区间为,
当时,,当时,,故D错误.
故选:BC.
12. 已知函数,则( )
A. 的定义域为B. 的图象关于轴对称
C. 的值域为D. 是减函数
【正确答案】AC
【分析】由,解出不等式解集即为的定义域,即可判断A;根据函数奇偶性的定义即可判断B;化简函数为,进而判断D;求出的值域,进而判断C.
【详解】由,即,解得,
所以函数的定义域为,故A正确;
又,
所以函数为奇函数,故B错误;
又,
因为函数在上为增函数,
所以函数在上为增函数,故D错误;
又,所以,即,
所以,即,
所以,
故函数的值域为,故C正确.
故选:AC.
三、填空题(本大题共4个小题,共20分)
13. 已知,则____________________________.
【正确答案】
【分析】分子、分母同除以,将代入化简即可.
【详解】因为,
所以,
故答案为.
本题主要考查同角三角函数之间的关系的应用,属于基础题. 同角三角函数之间的关系包含平方关系与商的关系,平方关系是正弦与余弦值之间的转换,商的关系是正余弦与正切之间的转换.
14. 已知奇函数,当时,,则__________.
【正确答案】1
【分析】根据奇函数的性质结合函数时的解析式,即可求得答案.
【详解】由题意得,
故答案为:1
15. “”是“”的_________________.(填“充分不必要条件”、“充要条件”、“必要不充分条件”、“既不充分也不必要条件”)
【正确答案】充分不必要条件
【分析】比较与大小关系,结合充分条件必要条件的定义判断结论.
【详解】,
所以时一定有,而时不一定有,
“”是“”的充分不必要条件.
故充分不必要条件
16. 若命题“”是假命题,则a的取值范围是_______.
【正确答案】
【分析】依题意可得是真命题,参变分离得到,再利用基本不等式计算可得;
【详解】解:因为命题“”是假命题,所以命题“”是真命题,即,所以,因为,当且仅当即时取等号,所以,即
故
四、解答题(本大题共6小题,共70分.解答过程应写出文字说明,证明过程或演算步骤)
17. 计算:
(1)+;
(2)
【正确答案】(1)0 (2)6
【分析】(1)由对数的运算性质和分数指数幂的运算性质可得答案
(2)由对数的运算法则和性质可得出答案.
【小问1详解】
原式=
【小问2详解】
原式=3+lg23⋅lg32+lg100=3+1+2=6.
18. 已知集合.
(1)当时,求;
(2)若,求的取值范围.
【正确答案】(1);
(2).
【分析】(1)解一元二次不等式求集合B,再由交运算求.
(2)根据包含关系,讨论、求参数范围即可.
【小问1详解】
由题设,
所以.
【小问2详解】
由,
当,则;
当,则;
综上,
19. 已知,α是第三象限角,求:
(1)的值;
(2)的值.
【正确答案】(1)2 (2)
【分析】(1)利用同角三角函数的基本关系求解;
(2)利用诱导公式化简求值.
【小问1详解】
因为,α是第三象限角,
则,
所以tan;
【小问2详解】
.
20. 已知函数的图象经过点,其中,且.
(1)求a的值;
(2)求函数的值域.
【正确答案】(1);
(2).
【分析】(1)利用给定函数结合,求解作答.
(2)由(1)求出函数解析式,再利用函数的单调性计算作答.
【小问1详解】
因函数的图象经过点,则,解得,
所以a的值为.
【小问2详解】
由(1)知,,则函数在R上单调递减,则当时,,
所以函数的值域为.
21. 已知函数,其中且.
(1)判断的奇偶性,并说明理由;
(2)若,求使成立的x的集合.
【正确答案】(1)奇函数,理由见解析;(2).
【分析】(1)先求得函数的定义域为关于原点对称,结合对数的运算,化简得到,即可得到结论;
(2)由,列出方程求得,得到,根据,得到不等式,即可求解.
【详解】(1)由题意,函数有意义,
则满足,解得,即的定义域为关于原点对称,
因为,
所以是定义域上的奇函数.
(2)由,可得,解得,
所以函数,
又由,则,可得,解得,
故不等式的解集为.
22. 某便民超市经销一种小袋装地方特色桃酥食品,每袋桃酥的成本为6元,预计当一袋桃酥的售价为元时,一年的销售量为万袋,并且全年该桃酥食品共需支付万元的管理费. 一年的利润一年的销售量售价(一年销售桃酥的成本一年的管理费).(单位:万元)
(1)求该超市一年的利润(万元)与每袋桃酥食品的售价的函数关系式;
(2)当每袋桃酥的售价为多少元时,该超市一年的利润最大,并求出的最大值.
【正确答案】(1);
(2)售价为9元时,利润最大为9万元
【分析】(1)直接由题目所给关系即可求得利润(万元)与售价的函数关系式;
(2)将函数关系式变形整理得,结合基本不等式即可求出最大值.
【小问1详解】
由题意知,分公司一年的利润L(万元)与售价x的函数关系式为;
【小问2详解】
,因为,所以,
当且仅当即时取等号,此时最大为9万元.当每件产品的售价为9元时,该分公司一年的利润最大,且最大利润9万元.
相关试卷
这是一份2024-2025学年贵州省毕节市金沙县高一上册期末考试数学检测试题,共4页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
这是一份2024-2025学年贵州省毕节市金沙县高一上册期末考试数学检测试题(附解析),共13页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
这是一份2023-2024学年贵州省毕节市金沙县高一上学期期末质量监测数学试题(含解析),共15页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。









