专题09 三角函数的图象与性质的综合应用（讲义）-2025年高考数学二轮复习讲练（新高考通用）

这是一份专题09 三角函数的图象与性质的综合应用（讲义）-2025年高考数学二轮复习讲练（新高考通用），文件包含专题09三角函数的图象与性质的综合应用讲义-2025年高考数学二轮复习讲练新高考通用原卷版docx、专题09三角函数的图象与性质的综合应用讲义-2025年高考数学二轮复习讲练新高考通用解析版docx等2份试卷配套教学资源，其中试卷共63页， 欢迎下载使用。
\l "_Tc187085888" 01考情透视·目标导航 PAGEREF _Tc187085888 \h 2
\l "_Tc187085889" 02知识导图·思维引航 PAGEREF _Tc187085889 \h 3
\l "_Tc187085890" 03 知识梳理·方法技巧 PAGEREF _Tc187085890 \h 4
\l "_Tc187085891" 04 真题研析·精准预测 PAGEREF _Tc187085891 \h 6
\l "_Tc187085892" 05 核心精讲·题型突破 PAGEREF _Tc187085892 \h 8
\l "_Tc187085893" 题型一：齐次化模型 PAGEREF _Tc187085893 \h 8
\l "_Tc187085894" 题型二：辅助角与最值问题 PAGEREF _Tc187085894 \h 9
\l "_Tc187085895" 题型三：与三角函数有关的最值问题 PAGEREF _Tc187085895 \h 9
\l "_Tc187085896" 题型四：绝对值与三角函数综合模型 PAGEREF _Tc187085896 \h 10
\l "_Tc187085897" 题型五：三角函数的综合性质 PAGEREF _Tc187085897 \h 12
\l "_Tc187085898" 题型六：换元法配凑角 PAGEREF _Tc187085898 \h 14
\l "_Tc187085899" 题型七：三倍角公式 PAGEREF _Tc187085899 \h 15
\l "_Tc187085900" 重难点突破：ω的取值与范围问题 PAGEREF _Tc187085900 \h 16
三角函数的图象与性质在高考中占据重要地位，是考查的重点和热点。高考对这部分内容的考查主要集中在两个方面：
1、三角函数的图象方面，这包括图象的变换问题以及根据图象来确定三角函数的解析式。这类问题通常以选择题和填空题的形式出现，考查学生对图象变换和解析式确定的理解和掌握。
2、三角函数的性质应用方面，这涉及利用三角函数的性质来求解三角函数的值、参数、最值、值域以及单调区间等问题。这类问题通常以解答题的形式出现，要求学生能够灵活运用三角函数的性质来解决问题。
此外，三角恒等变换的求值和化简也是高考命题的热点之一。这部分内容既可以单独命题，以选择题或填空题的形式呈现，难度相对较低；也可以作为工具，与三角函数及解三角形相结合，求解最值、范围等问题，这时多以解答题的形式出现，难度适中。
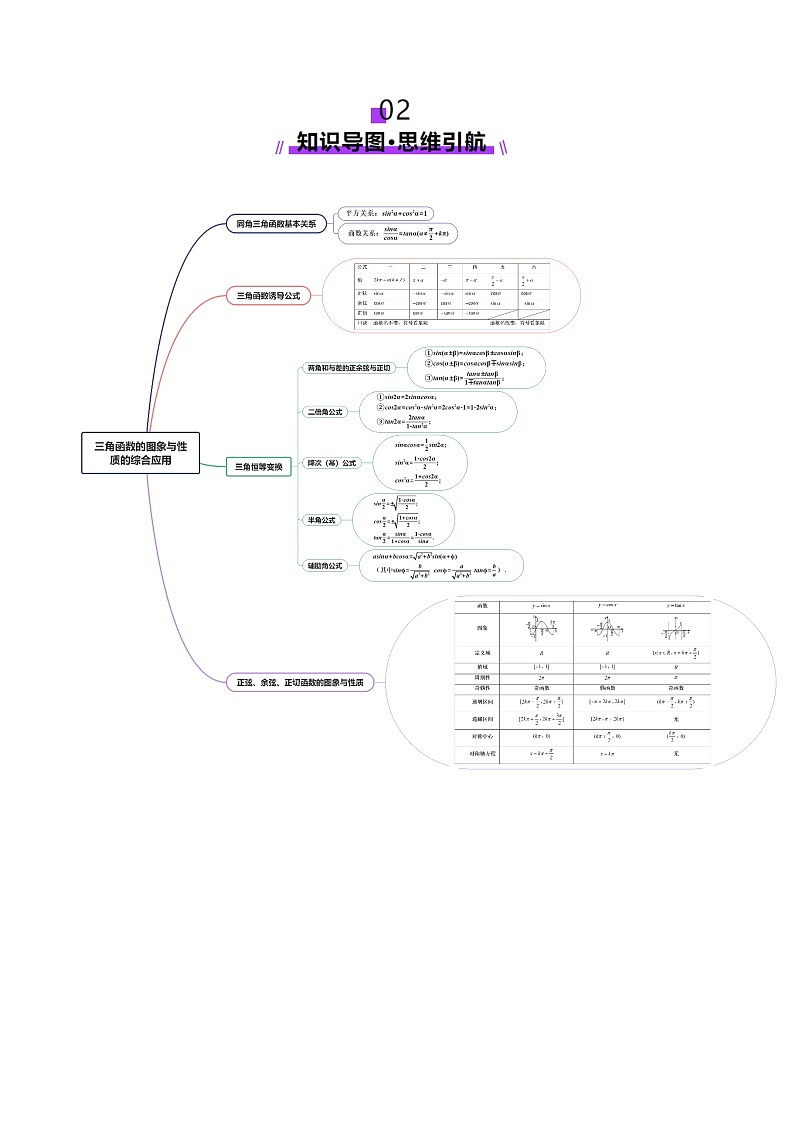
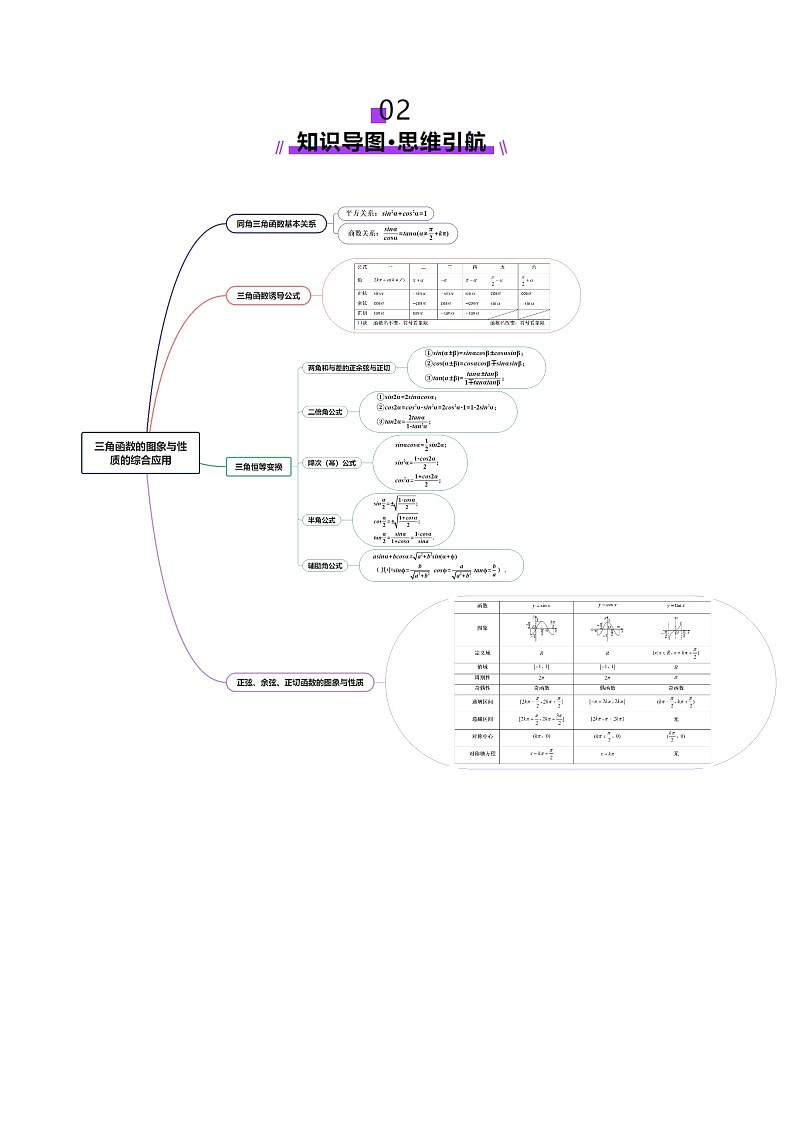
1、三角函数图象的变换
（1）将的图象变换为的图象主要有如下两种方法：
（2）平移变换
函数图象的平移法则是“左加右减、上加下减”，但是左右平移变换只是针对作的变换；
（3）伸缩变换
①沿轴伸缩时，横坐标伸长或缩短为原来的（倍）（纵坐标不变）；
②沿轴伸缩时，纵坐标伸长或缩短为原来的（倍）（横坐标不变）．
（4）注意平移前后两个函数的名称是否一致，若不一致，应用诱导公式化为同名函数再平移．
2、三角函数的单调性
（1）三角函数的单调区间
的单调递增区间是，
单调递减区间是；
的单调递增区间是，
单调递减区间是；
的单调递增区间是．
（2）三角函数的单调性有时也要结合具体的函数图象如结合，，
，的图象进行判断会很快得到正确答案．
3、求三角函数最值的基本思路
（1）将问题化为的形式，结合三角函数的图象和性质求解.
（2）将问题化为关于或的二次函数的形式，借助二次函数的图象和性质求解.
（3）利用导数判断单调性从而求解.
4、对称性及周期性常用结论
（1）对称与周期的关系
正弦曲线、余弦曲线相邻的两个对称中心、相邻的两条对称轴之间的距离是半个周期，相邻的对称中心与对称轴之间的距离是四分之一个周期；正切曲线相邻两个对称中心之间的距离是半个周期.
（2）与三角函数的奇偶性相关的结论
若为偶函数，则有；若为奇函数，则有.
若为偶函数，则有；若为奇函数，则有.
若为奇函数，则有．
5、已知三角函数的单调区间求参数取值范刪的三种方法
（1）子集法：求出原函数相应的单调区间，由已知区间是所求某区间的子集，列不等式（组）求解．
（2）反子集法：由所给区间求出整体角的范围，由该范围是某相应正弦、余弦函数的某个单调区间的子集，列不等式（组）求解．
（3）周期性：由所给区间的两个端点到其相应对称中心的距离不超过个周期列不等式（组）求解.
1．（2024年高考全国甲卷数学（理）真题）已知，则（ ）
A．B．C．D．
2．（2024年北京高考数学真题）设函数.已知，，且的最小值为，则（ ）
A．1B．2C．3D．4
3．（2024年天津高考数学真题）已知函数的最小正周期为．则在区间上的最小值是（ ）
A．B．C．0D．
4．（2024年新课标全国Ⅱ卷数学真题）设函数，，当时，曲线与恰有一个交点，则（ ）
A．B．C．1D．2
5．（2024年新课标全国Ⅰ卷数学真题）当时，曲线与的交点个数为（ ）
A．3B．4C．6D．8
6．（2024年新课标全国Ⅰ卷数学真题）已知，则（ ）
A．B．C．D．
7．（多选题）（2024年新课标全国Ⅱ卷数学真题）对于函数和，下列说法中正确的有（ ）
A．与有相同的零点B．与有相同的最大值
C．与有相同的最小正周期D．与的图象有相同的对称轴
8．（2024年北京高考数学真题）在平面直角坐标系中，角与角均以为始边，它们的终边关于原点对称.若，则的最大值为 ．
9．（2024年高考全国甲卷数学（文）真题）函数在上的最大值是 ．
10．（2024年新课标全国Ⅱ卷数学真题）已知为第一象限角，为第三象限角，，，则 .
11．（2023年北京高考数学真题）已知命题若为第一象限角，且，则．能说明p为假命题的一组的值为 ， ．
12．（2023年北京高考数学真题）设函数．
(1)若，求的值．
(2)已知在区间上单调递增，，再从条件①、条件②、条件③这三个条件中选择一个作为已知，使函数存在，求的值．
条件①：；
条件②：；
条件③：在区间上单调递减．
注：如果选择的条件不符合要求，第（2）问得0分；如果选择多个符合要求的条件分别解答，按第一个解答计分．
题型一：齐次化模型
【典例1-1】（2024·高三·江西宜春·期末）已知，则（ ）
A．1B．C．2D．
【典例1-2】（2024·高三·河北沧州·期中）已知，则（ ）
A．B．C．D．
齐次分式：分子分母的正余弦次数相同，例如：
（一次显型齐次化）
或者（二次隐型齐次化）
这种类型题，分子分母同除以（一次显型）或者（二次隐型），构造成的代数式，这个思想在圆锥曲线里面关于斜率问题处理也经常用到.
【变式1-2】（2024·陕西安康·三模）已知，则（ ）
A．6B．C．D．2
【变式1-3】若，则的值为（ ）
A．B．C．D．
1．设，若，则（ ）
A．B．C．D．
题型二：辅助角与最值问题
【典例2-1】若函数在处取得最大值，则 .
【典例2-2】（2024·高三·江西萍乡·期中）设，且，则实数的取值范围是 ．
第一类：一次辅助角:=．（其中）
第二类：二次辅助角
【变式2-1】（2024·高三·山东临沂·期中）已知关于x的方程有解，则的最小值为 .
【变式2-2】已知，求的最大值 .
1．[新考法]（2024·高三·江苏苏州·开学考试）设角、均为锐角，则的范围是 ．
题型三：与三角函数有关的最值问题
【典例3-1】已知函数，则的最小值是 ．
【典例3-2】函数的最大值是（ ）
A．B．C．D．
三角函数最值问题，一直是高考中的难点与重点。这类题目常融合三角恒等变换，结合函数、导数与不等式，求解不易。通常，处理三角函数最值问题，可采用以下策略：化一简化法、变量替换法（换元）、主元突出法、图形与数值结合法，以及导数求极值法。
【变式3-1】已知，则的最大值为
【变式3-2】在中，的最大值是（ ）
A．B．C．2D．
1．已知函数（），则函数的最大值为 .
2．函数的值域是 ．
题型四：绝对值与三角函数综合模型
【典例4-1】已知函数，则下列说法正确的是（ ）
A．的最小正周期为B．的最小值为
C．D．在上有解
【典例4-2】（2024·高三·上海宝山·开学考试）已知，给出下述四个结论:
①是偶函数; ②在上为减函数;
③在上为增函数; ④的最大值为.
其中所有正确结论的编号是（ ）
A．①②④B．①③④C．①②③D．①④
关于和，如图，将图像中轴上方部分保留，轴下方部分沿着轴翻上去后得到，故是最小正周期为的函数，同理是最小正周期为的函数；是将图像中轴右边的部分留下，左边的删除，再将轴右边图像作对称至左边，故不是周期函数.我们可以这样来表示：
，
【变式4-1】关于函数有下述四个结论：
①是偶函数；
②在区间上单调；
③函数的最大值为M，最小值为m，则；
④若，则函数在上有4个零点．
其中所有正确结论的编号是（ ）
A．①④B．①③C．②④D．①②③
【变式4-2】关于函数，其中有下述四个结论：
①是偶函数； ②在区间上是严格增函数；
③在有3个零点； ④的最小正周期为．
其中所有正确结论的编号是（ ）．
A．①②B．②④C．①④D．①③
1．（多选题）已知函数，则（ ）
A．是的一个周期B．是的一条对称轴
C．的值域为D．在上单调递减
题型五：三角函数的综合性质
【典例5-1】（多选题）已知函数，若及其导函数的部分图象如图所示，则（ ）
A．
B．函数在上单调递减
C．的图象关于点中心对称
D．的最大值为
【典例5-2】（多选题）已知函数，若，且，则函数的最小正周期可能是（ ）
A．B．C．D．
三角函数的综合性质解题，关键在于掌握其基本关系、图像变换及周期性。解题时，先识别函数类型，利用诱导公式化简，再结合图像分析性质，如单调性、最值等。最后，灵活运用三角函数公式求解，注意计算准确性。
【变式5-1】（多选题）已知函数的最小正周期为，其图象关于直线对称，且对于恒成立，则（ ）
A．函数为偶函数
B．当时，的值域为
C．将函数的图象向右平移个单位长度后可得函数的图象
D．将函数的图象上所有点的横坐标伸长为原来的2倍，纵坐标不变，得到的函数图象关于点对称
【变式5-2】（多选题）已知函数（，）图象的两条对称轴间距离的最小值为，且为的一个零点，则（ ）
A．的最小正周期为
B．
C．在上单调递增
D．当时，曲线与直线的所有交点的横坐标之和为
1．[新考法]（多选题）已知函数，则（ ）
A．的图象关于直线对称
B．的最大值为
C．在上单调递增
D．方程在上最多有4个解
2．[新考法]（多选题）设函数的最小正零点为，则（ ）
A．的图象过定点B．的最小正周期为
C．是等比数列D．的前项和为
题型六：换元法配凑角
【典例6-1】[新考法]若，则 .
【典例6-2】已知，且，则 .
三角函数“凑角拆角”问题，常规配凑解法繁琐。采用换元法，可简化步骤，快速求解。
【变式6-1】已知，则 .
【变式6-2】设，若，则的值为 ．
1．已知，，则 .
题型七：三倍角公式
【典例7-1】著名数学家华罗庚先生被誉为“中国现代数学之父”，他倡导的“0.618优选法”在生产和科研实践中得到了非常广泛的应用．黄金分割比，现给出三倍角公式和二倍角角公式，则t与的关系式正确的为（ ）
A．B．C．D．
【典例7-2】（多选题）（2024·高三·浙江宁波·期末）已知为坐标原点，曲线：，，为曲线上动点，则（ ）
A．曲线关于y轴对称B．曲线的图象具有3条对称轴
C．D．的最大值为
三倍角公式: (1) .
(2) .
(3) .
【变式7-1】若不等式对任意恒成立，则实数的取值范围是 .
1．已知为锐角，且.则 .
重难点突破：w的取值与范围问题
【典例8-1】已知函数在区间上是增函数，若函数在上的图象与直线有且仅有一个交点，则的范围为（ ）
A．B．C．D．
【典例8-2】（2024·高三·河北石家庄·期中）已知函数在上恰有2个零点，则的范围为（ ）
A．B．
C．D．
1、在区间内没有零点
同理，在区间内没有零点
2、在区间内有个零点
同理在区间内有个零点

3、在区间内有个零点

同理在区间内有个零点
4、已知一条对称轴和一个对称中心，由于对称轴和对称中心的水平距离为，则．
5、已知单调区间，则.
【变式8-1】（2024·新疆阿勒泰·三模）已知，若函数在区间上有且只有个零点，则的范围为（ ）
A．B．
C．D．
【变式8-2】（2024·高三·福建厦门·期中）若直线是曲线的一条对称轴，且函数在区间上不单调，则的最小值为（ ）
A．7B．9C．11D．15
1．若函数在内存在最小值但无最大值，则的范围是
2．已知（其中），其函数图像关于直线对称，若函数在区间上有且只有三个零点，则的范围为 ．
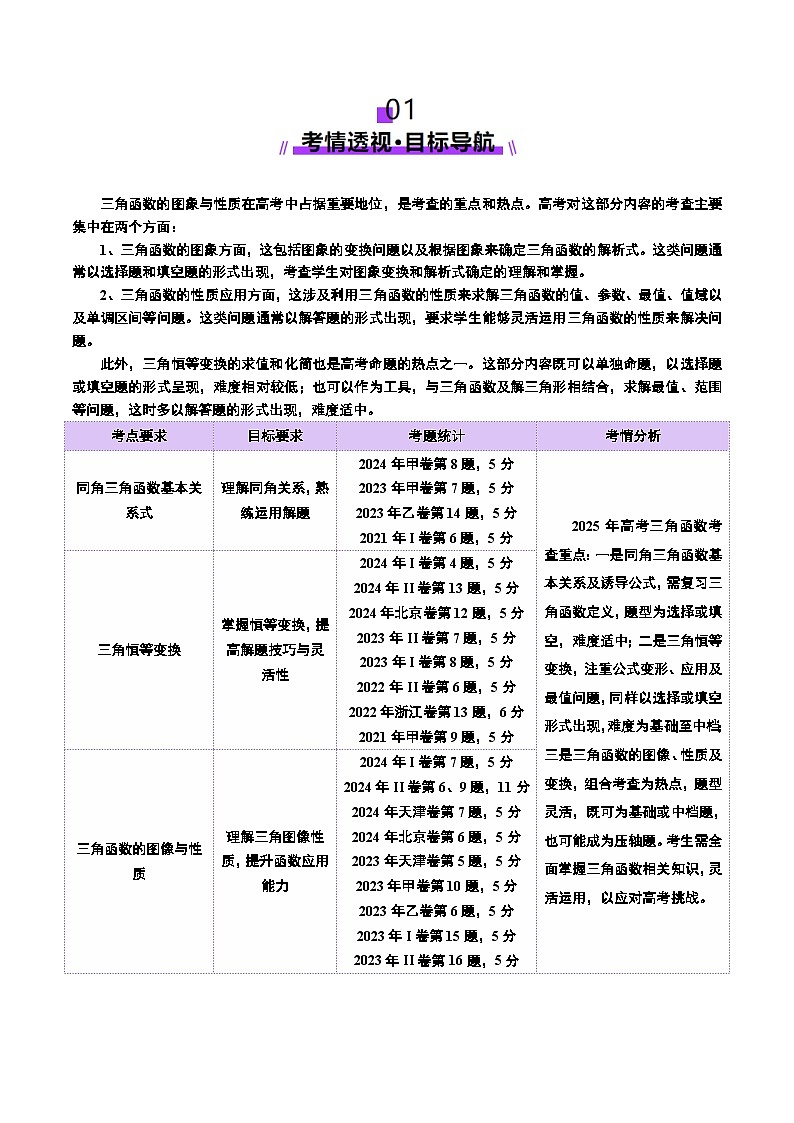
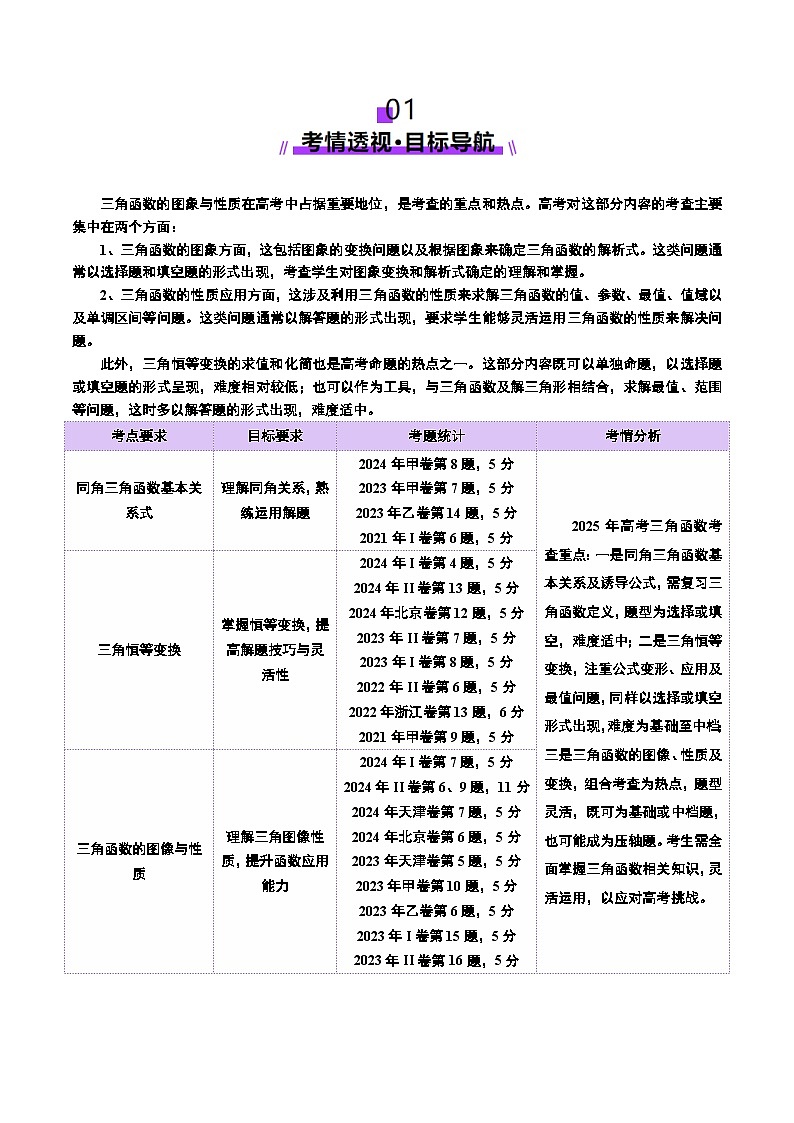
考点要求
目标要求
考题统计
考情分析
同角三角函数基本关系式
理解同角关系，熟练运用解题
2024年甲卷第8题，5分
2023年甲卷第7题，5分
2023年乙卷第14题，5分
2021年I卷第6题，5分
2025年高考三角函数考查重点：一是同角三角函数基本关系及诱导公式，需复习三角函数定义，题型为选择或填空，难度适中；二是三角恒等变换，注重公式变形、应用及最值问题，同样以选择或填空形式出现，难度为基础至中档；三是三角函数的图像、性质及变换，组合考查为热点，题型灵活，既可为基础或中档题，也可能成为压轴题。考生需全面掌握三角函数相关知识，灵活运用，以应对高考挑战。
三角恒等变换
掌握恒等变换，提高解题技巧与灵活性
2024年I卷第4题，5分
2024年II卷第13题，5分
2024年北京卷第12题，5分
2023年II卷第7题，5分
2023年I卷第8题，5分
2022年II卷第6题，5分
2022年浙江卷第13题，6分
2021年甲卷第9题，5分
三角函数的图像与性质
理解三角图像性质，提升函数应用能力
2024年I卷第7题，5分
2024年II卷第6、9题，11分
2024年天津卷第7题，5分
2024年北京卷第6题，5分
2023年天津卷第5题，5分
2023年甲卷第10题，5分
2023年乙卷第6题，5分
2023年I卷第15题，5分
2023年II卷第16题，5分