专题10 正余弦定理在解三角形中的高级灵活应用与最值问题（讲义）-2025年高考数学二轮复习讲练（新高考通用）

这是一份专题10 正余弦定理在解三角形中的高级灵活应用与最值问题（讲义）-2025年高考数学二轮复习讲练（新高考通用），文件包含专题10正余弦定理在解三角形中的高级灵活应用与最值问题讲义-2025年高考数学二轮复习讲练新高考通用原卷版docx、专题10正余弦定理在解三角形中的高级灵活应用与最值问题讲义-2025年高考数学二轮复习讲练新高考通用解析版docx等2份试卷配套教学资源，其中试卷共100页， 欢迎下载使用。
\l "_Tc187093654" 01考情透视·目标导航 PAGEREF _Tc187093654 \h 2
\l "_Tc187093655" 02知识导图·思维引航 PAGEREF _Tc187093655 \h 3
\l "_Tc187093656" 03 知识梳理·方法技巧 PAGEREF _Tc187093656 \h 4
\l "_Tc187093657" 04 真题研析·精准预测 PAGEREF _Tc187093657 \h 5
\l "_Tc187093658" 05 核心精讲·题型突破 PAGEREF _Tc187093658 \h 8
\l "_Tc187093659" 题型一：倍长定比分线模型 PAGEREF _Tc187093659 \h 8
\l "_Tc187093660" 题型二：倍角定理与正弦平方差 PAGEREF _Tc187093660 \h 9
\l "_Tc187093661" 题型三：角平分线模型与张角定理 PAGEREF _Tc187093661 \h 11
\l "_Tc187093662" 题型四：隐圆问题 PAGEREF _Tc187093662 \h 13
\l "_Tc187093663" 题型五：正切比值与和差问题 PAGEREF _Tc187093663 \h 13
\l "_Tc187093664" 题型六：四边形定值和最值与托勒密定理 PAGEREF _Tc187093664 \h 14
\l "_Tc187093665" 题型七：边角特殊，构建坐标系 PAGEREF _Tc187093665 \h 17
\l "_Tc187093666" 题型八：利用正、余弦定理求解与三角形的周长、面积有关的问题 PAGEREF _Tc187093666 \h 18
\l "_Tc187093667" 题型九：三角形的形状判定 PAGEREF _Tc187093667 \h 19
\l "_Tc187093668" 题型十：三角形中的几何计算 PAGEREF _Tc187093668 \h 21
\l "_Tc187093669" 题型十一：中线长定理与余弦和为0 PAGEREF _Tc187093669 \h 23
\l "_Tc187093670" 重难点突破：利用正，余弦定理求解三角形中的最值或范围 PAGEREF _Tc187093670 \h 25
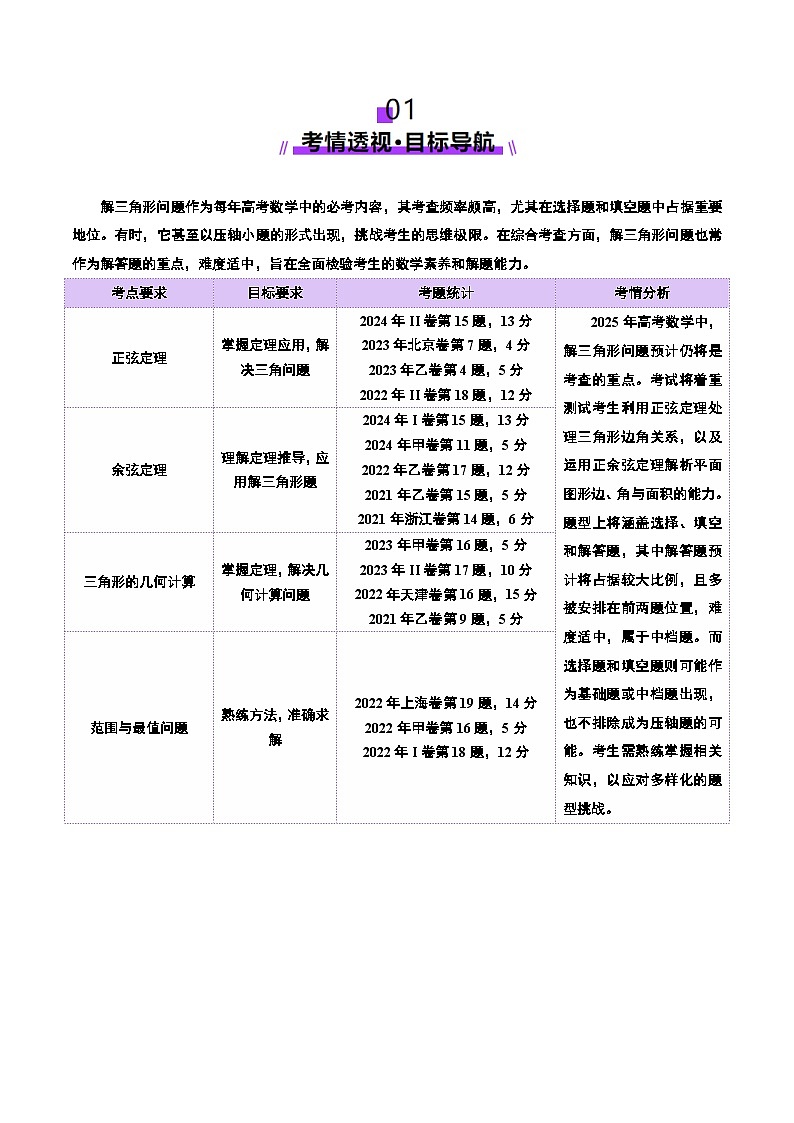
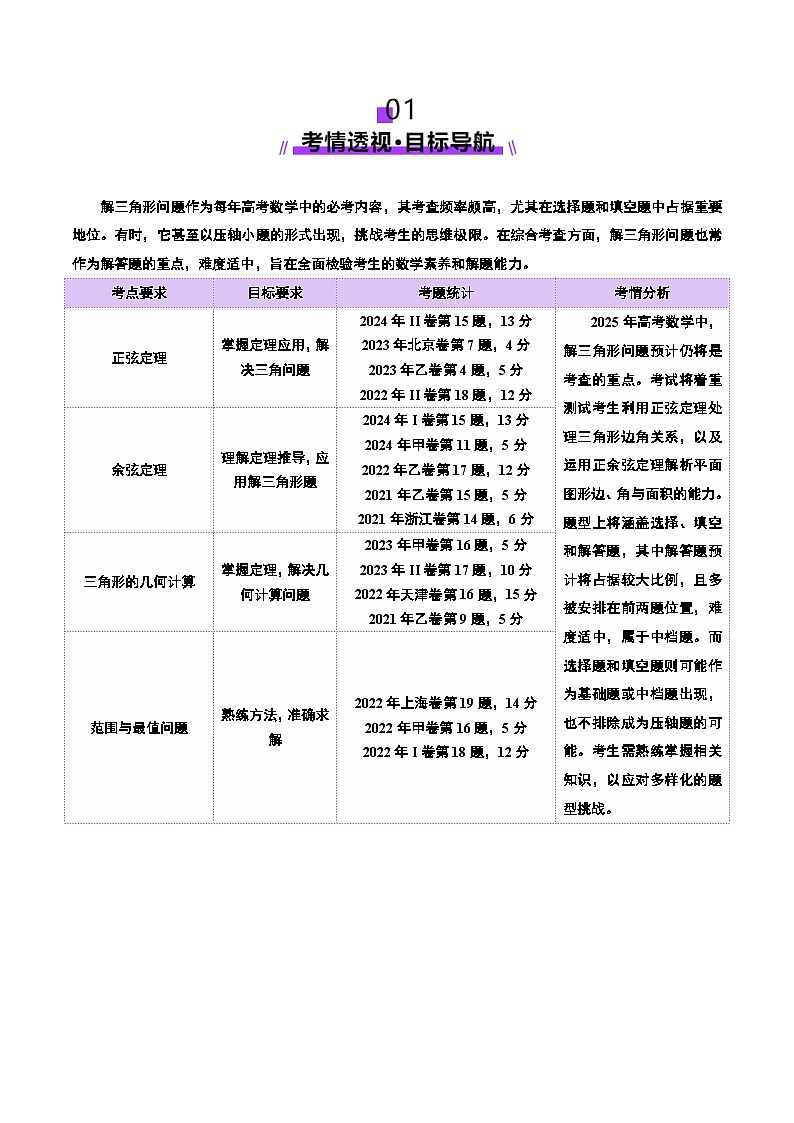
解三角形问题作为每年高考数学中的必考内容，其考查频率颇高，尤其在选择题和填空题中占据重要地位。有时，它甚至以压轴小题的形式出现，挑战考生的思维极限。在综合考查方面，解三角形问题也常作为解答题的重点，难度适中，旨在全面检验考生的数学素养和解题能力。
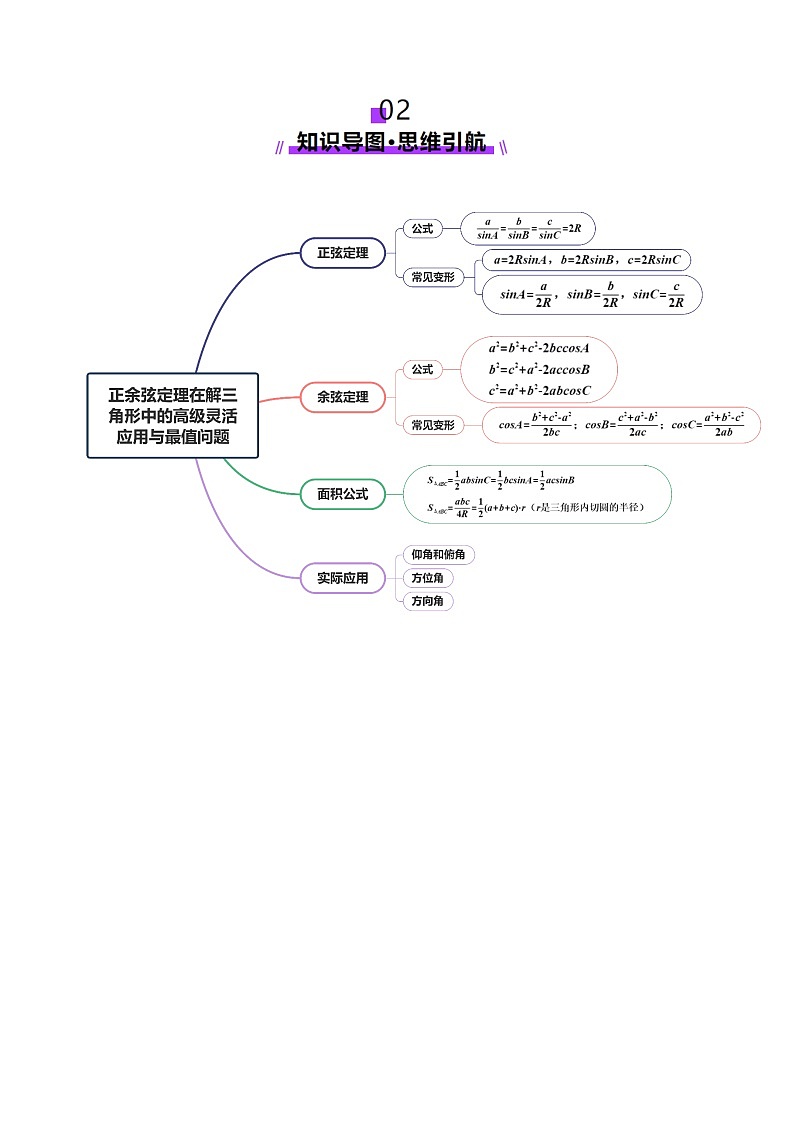
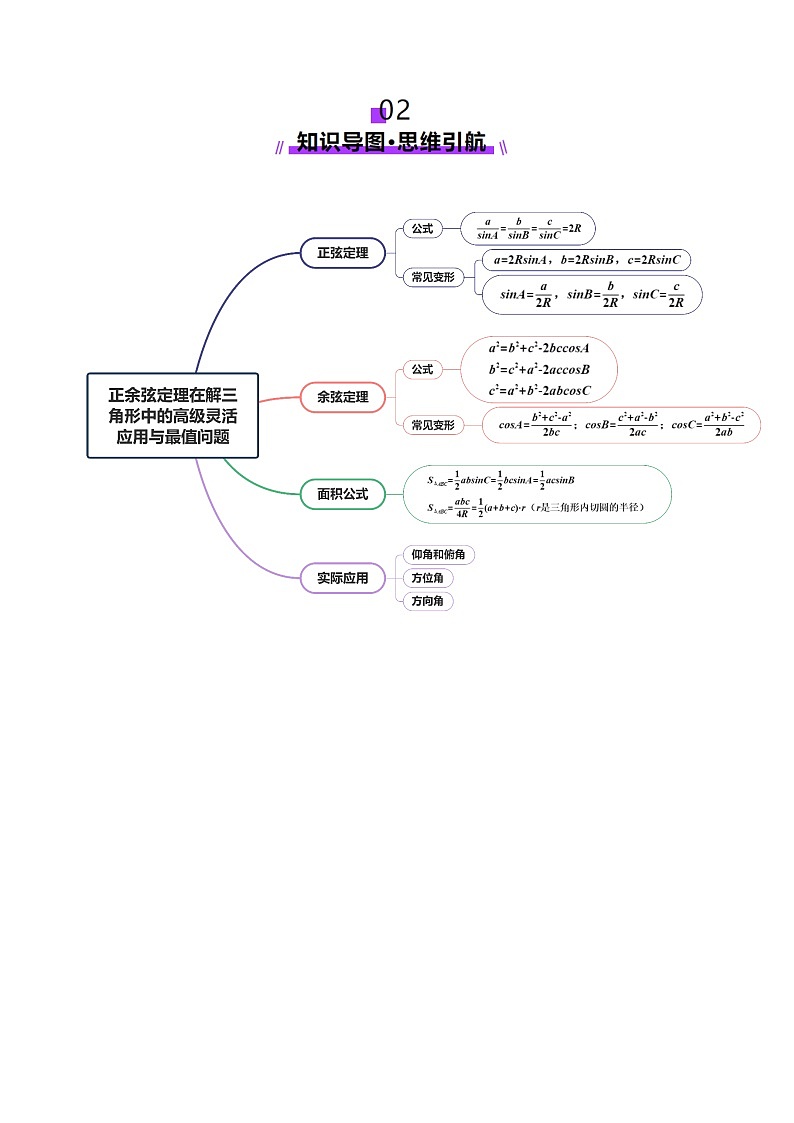
1、正弦定理和余弦定理的主要作用，是将三角形中已知条件的边、角关系转化为角的关系或边的关系，基本思想是方程思想，即根据正弦定理、余弦定理列出关于未知元素的方程，通过解方程求得未知元素．
2、与三角形面积或周长有关的问题，一般要用到正弦定理或余弦定理，进行边和角的转化．要适当选用公式，对于面积公式，一般是已知哪一个角就使用哪个公式．
3、对于利用正、余弦定理解三角形中的最值与范围问题，主要有两种解决方法：一是利用基本不等式，求得最大值或最小值；二是将所求式转化为只含有三角形某一个角的三角函数形式，结合角的范围，确定所求式的范围．
4、利用正、余弦定理解三角形，要注意灵活运用面积公式，三角形内角和、基本不等式、二次函数等知识．
5、正弦定理和余弦定理是求解三角形周长或面积最值问题的杀手锏，要牢牢掌握并灵活运用．利用三角公式化简三角恒等式，并结合正弦定理和余弦定理实现边角互化，再结合角的范围、辅助角公式、基本不等式等求其最值．
6、三角形中的一些最值问题，可以通过构建目标函数，将问题转化为求函数的最值，再利用单调性求解．
7、“坐标法”是求解与解三角形相关最值问题的一条重要途径．充分利用题设条件中所提供的特殊边角关系，建立恰当的直角坐标系，选取合理的参数，正确求出关键点的坐标，准确表示出所求的目标，再结合三角形、不等式、函数等知识求其最值．
1．（2024年高考全国甲卷数学（理）真题）在中,内角所对的边分别为，若，，则（ ）
A．B．C．D．
2．（2024年北京高考数学真题）在中，内角的对边分别为，为钝角，，．
(1)求；
(2)从条件①、条件②、条件③这三个条件中选择一个作为已知，使得存在，求的面积．
条件①：；条件②：；条件③：．
注：如果选择的条件不符合要求，第（2）问得0分；如果选择多个符合要求的条件分别解答，按第一个解答计分．
3．（2024年新课标全国Ⅱ卷数学真题）记的内角A，B，C的对边分别为a，b，c，已知．
(1)求A．
(2)若，，求的周长．
4．（2024年新课标全国Ⅰ卷数学真题）记的内角A、B、C的对边分别为a，b，c，已知，
(1)求B；
(2)若的面积为，求c．
5．（2023年高考全国甲卷数学（文）真题）记的内角的对边分别为，已知．
(1)求；
(2)若，求面积．
6．（2023年高考全国乙卷数学（理）真题）在中，已知，，.
(1)求；
(2)若D为BC上一点，且，求的面积.
7．（2023年新课标全国Ⅰ卷数学真题）已知在中，．
(1)求；
(2)设，求边上的高．
8．（2023年北京高考数学真题）在中，，则（ ）
A．B．C．D．
9．（2023年高考全国乙卷数学（文）真题）在中，内角的对边分别是，若，且，则（ ）
A．B．C．D．
10．（2023年高考全国甲卷数学（理）真题）在中，，的角平分线交BC于D，则 ．
11．（2022年新高考浙江数学高考真题）我国南宋著名数学家秦九韶，发现了从三角形三边求面积的公式，他把这种方法称为“三斜求积”，它填补了我国传统数学的一个空白．如果把这个方法写成公式，就是，其中a，b，c是三角形的三边，S是三角形的面积．设某三角形的三边，则该三角形的面积 ．
12．（2022年高考全国甲卷数学（理）真题）已知中，点D在边BC上，．当取得最小值时， ．
13．（2022年新高考全国II卷数学真题）记的内角A，B，C的对边分别为a，b，c，分别以a，b，c为边长的三个正三角形的面积依次为，已知．
(1)求的面积；
(2)若，求b．
14．（2022年高考全国乙卷数学（文）真题）记的内角A，B，C的对边分别为a，b，c﹐已知．
(1)若，求C；
(2)证明：
15．（2022年新高考全国I卷数学真题）记的内角A，B，C的对边分别为a，b，c，已知．
(1)若，求B；
(2)求的最小值．
题型一：倍长定比分线模型
【典例1-1】设a，b，c分别为的内角A，B，C的对边，AD为BC边上的中线，c＝1，，．
(1)求AD的长度；
(2)若E为AB上靠近B的四等分点，G为的重心，连接EG并延长与AC交于点F，求AF的长度．
【典例1-2】在中，内角A，B，C的对边分别为a，b，c，且满足，
(1)求角B的大小；
(2)若，D为边AB上一点，且，求的值．
如图，若在边上，且满足，，则延长至，使，连接，易知∥，且，．．
【变式1-1】在① ，② ，这两个条件中任选一个，补充在下面的问题中，并解答问题．
在中，内角的对边分别为，且满足____．
(1)求；
(2)若的面积为在边上，且 ， ，求的值．
注：如果选择多个条件分别解答，按第一个解答记分．
1．在中，角所对的边分别为，且是的中点，，则 ， .
题型二：倍角定理与正弦平方差
【典例2-1】从①；②；③，这三个条件中任选一个，补充在下面的横线上并解答问题．
在锐角中，角所对的边分别为，且________．
(1)证明：；
(2)求的取值范围．
注：如果选择多个条件分别解答，按第一个解答计分．
【典例2-2】已知a，b，c分别为三个内角A，B，C的对边，．
(1)证明：；
(2)若，且为锐角三角形，求的取值范围．
，这样的三角形称为“倍角三角形”．
推论1：
推论2：
正弦平方差：
【变式2-1】在中，AB＝4，AC＝3．
(1)若，求的面积；
(2)若A＝2B，求BC的长．
【变式2-2】在锐角中，角，，所对的边为，，，且．
(1)证明：；
(2)求的取值范围．
1．在锐角中，角所对的边为，且.
(1)证明:
(2)若，求的取值范围.
题型三：角平分线模型与张角定理
【典例3-1】在中，角，，所对的边分别为，，，且.
(1)求角的大小：
(2)若，，，求的值；
(3)设是边上一点，为角平分线且，求的值.
【典例3-2】已知在中，角A，B，C的对边分别为a，b，c，且
(1)求角B；
(2)若点D在上，为的角平分线，，求的最小值．
角平分线张角定理：如图，为平分线，（参考一轮复习）
斯库顿定理：如图，是的角平分线，则，可记忆：中方=上积一下积．
【变式3-1】（2024·河北沧州·模拟预测）在中，角A，B，C的对边分别为a，b，c，已知．
(1)求证：；
(2)若的角平分线交AC于点D，且，，求BD的长．
【变式3-2】 中，内角A，B，C所对的边分别为a，b，c.已知.
(1)求的值；
(2)若BD是的角平分线.
（i）证明：；
（ii）若，求的最大值.
1．在△ABC中，内角A，B，C所对的边分别为a，b，c，且
(1)求C；
(2)若△ABC的三条角平分线相交于点O，AB＝7，OAB的面积为，求OC．
题型四：隐圆问题
【典例4-1】（2024·四川眉山·三模）阿波罗尼奥斯是与阿基米德、欧几里得齐名的古希腊数学家，以他姓名命名的阿氏圆是指平面内到两定点的距离的比值为常数的动点的轨迹．已知在中，角、、所对的边分别为、、，且，，则面积的最大值为（ ）
A．B．C．D．
【典例4-2】在平面四边形中，连接对角线，已知，，，，则对角线的最大值为（ ）
A．27B．16C．10D．25
若三角形中出现，且为定值，则点C位于阿波罗尼斯圆上．
【变式4-1】已知中，，为的重心，且满足，则的面积的最大值为______.
【变式4-2】已知等边的边长为2，点G是内的一点，且，点P在所在的平面内且满足，则的最大值为________.
1．在平面四边形ABCD中，， ，．若， 则的最小值为____．
题型五：正切比值与和差问题
【典例5-1】在△ABC中，且，则△ABC面积的最大值为 ．
【典例5-2】已知在锐角△ABC中，角A，B，C的对边分别为a，b，c，若，则 ，的最小值为 .
定理1：
定理2：
定理3：（正切恒等式）中，．
【变式5-1】（2024·浙江·模拟预测）在锐角三角形中，角的对边分别为，若，则的最小值是 ．
【变式5-2】在中，角所对的边分别为，若，且，则 ．
1．在锐角中，分别为角所对的边，，且的面积．
(1)若，求；
(2)求的最大值．
题型六：四边形定值和最值与托勒密定理
【典例6-1】克罗狄斯托勒密（约90-168年）是希腊著名的数学家、天文学家和地理学家．托勒密定理是欧几里得几何中的重要定理，定理内容如下：任意一凸四边形，两组对边乘积的和不小于两对角线的乘积，当且仅当四点共圆时，等号成立．已知在凸四边形中，，，，，则的最大值为（ ）
A．B．C．D．
【典例6-2】托勒密是古希腊天文学家、地理学家、数学家，托勒密定理就是由其名字命名，该定理原文：圆的内接四边形中，两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和.其意思为：圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积.从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式，托勒密定理实质上是关于共圆性的基本性质.已知四边形ABCD的四个顶点在同一个圆的圆周上，AC、BD是其两条对角线，，且为正三角形，则四边形ABCD的面积为（ ）
A．B．16C．D．12
正常的四边形我们不去解释，只需多一次余弦定理即可，我们需要注意一些圆内接的四边形，尤其是拥有对角互补的四边形，尤其一些四边形还需要引入托勒密定理．
托勒密定理：在四边形中，有，当且仅当四边形ABCD四点共圆时，等号成立．
【变式6-1】如图．在平面四边形中，．设，证明：为定值．
【变式6-2】如图，平面四边形的对角线分别为，，其中，，．

(1)若，的面积为，求的面积；
(2)若，，求的值．
1．克罗狄斯·托勒密是古希腊著名数学家、天文学家和地理学家，他在所著的《天文集》中讲述了制作弦表的原理，其中涉及如下定理：任意凸四边形中，两条对角线的乘积小于或等于两组对边乘积之和，当且仅当凸四边形的对角互补时取等号，后人称之为托勒密定理的推论．如图，四边形ABCD内接于半径为的圆，，，，则四边形ABCD的周长为（ ）
A．B．C．D．
题型七：边角特殊，构建坐标系
【典例7-1】已知三角形中，，角的平分线交于点，若，则三角形面积的最大值为（ ）
A．1B．2C．3D．4
【典例7-2】在中，，点在边上，且，若，则长度的最大值为（ ）
A．3B．4C．5D．6
利用坐标法求出轨迹方程
【变式7-1】已知△ABC内角A，B，C的对边分别为a，b，c，点G是△ABC的重心，且.
(1)若，求tan∠GAC的值；
(2)求cs∠ACB的取值范围.
1．在中，，，，M是所在平面上的动点，则的最小值为________．
题型八：利用正、余弦定理求解与三角形的周长、面积有关的问题
【典例8-1】（2024·高三·河北沧州·期中）记的内角，，所对的边分别为，，，已知．
(1)求A；
(2)若的面积为，，求的周长．
【典例8-2】在中，角对应的边分别为．已知．
(1)求；
(2)若点为边的中点，且，，求的面积．
与三角形面积或周长有关的问题，一般要用到正弦定理或余弦定理，进行边和角的转化．要适当选用公式，对于面积公式，一般是已知哪一个角就使用哪个公式．
【变式8-1】已知的三个角A，B，C的对边分别是a，b，c，且．
(1)若，求C；
(2)若，，求的面积．
【变式8-2】（2024·四川眉山·一模）在中，内角，，所对的边分别为，，，已知，且.
(1)求；
(2)若的外接圆半径为，周长为，且，求.
1．记的内角A，B，C的对边分别为a，b，c，已知.
(1)求A；
(2)若，，求的周长.
题型九：三角形的形状判定
【典例9-1】已知的三条边和与之对应的三个角满足等式则此三角形的形状是（ ）
A．等腰三角形B．直角三角形
C．等腰或直角三角形D．等腰直角三角形
【典例9-2】（2024·高三·福建南平·期中）在△中，内角的对边分别为，已知向量共线，则△的形状为（ ）
A．等边三角形B．钝角三角形
C．有一个内角是的直角三角形D．等腰直角三角形
余弦定理判定：三角形三条边从小到大排列，即，
若，则是锐角三角形；
若，则是直角三角形；
若，则是钝角三角形；
【变式9-1】（2024·高三·上海闵行·期中）在中，已知，且，则的形状为（ ）
A．直角三角形B．等腰直角三角形
C．有一个角为的直角三角形D．等边三角形
【变式9-2】在中，角，，分别为，，三边所对的角，，则的形状是（ ）
A．等腰三角形但一定不是直角三角形
B．等腰直角三角形
C．直角三角形但一定不是等腰三角形
D．等腰三角形或直角三角形
1．已知分别是三个内角的对边，下列关于的形状判断一定正确的为（ ）
A．，则为直角三角形
B．，则为等腰三角形
C．，则为直角三角形
D．，则为等腰三角形
2．已知的三个内角A，B，C所对的边分别为a，b，c，满足，且，则的形状为（ ）
A．等边三角形B．顶角为的等腰三角形
C．顶角为的等腰三角形D．等腰直角三角形
题型十：三角形中的几何计算
【典例10-1】（2024·高三·安徽·期中）如图，在平面四边形中，与的交点为E，平分，，．
(1)证明：；
(2)若，求．
【典例10-2】在平面四边形中，，，且.
(1)求的长；
(2)若为的中点，求.
解决三角形中几何计算的方法：
方法一：两次应用余弦定理是一种典型的方法，充分利用了三角形的性质和正余弦定理的性质解题；
方法二：等面积法是一种常用的方法，很多数学问题利用等面积法使得问题转化为更为简单的问题，相似是三角形中的常用思路；
方法三：正弦定理和余弦定理相结合是解三角形问题的常用思路；
方法四：构造辅助线作出相似三角形，结合余弦定理和相似三角形是一种确定边长比例关系的不错选择；
方法五：平面向量是解决几何问题的一种重要方法，充分利用平面向量基本定理和向量的运算法则可以将其与余弦定理充分结合到一起；
方法六：建立平面直角坐标系是解析几何的思路，利用此方法数形结合充分挖掘几何性质使得问题更加直观化.
【变式10-1】（2024·江苏扬州·模拟预测）如图，四边形中，已知，．
(1)若的面积为，求的周长；
(2)若，，，求的值．
【变式10-2】如图所示，在中，设分别为内角的对边，已知，．
(1)求角；
(2)若，过作的垂线并延长到点，使四点共圆，与交于点，求四边形的面积．
1．在中，.
(1)求角B的大小；
(2)若E为的中点，F是边上的点，且满足，，求的值.
题型十一：中线长定理与余弦和为0
【典例11-1】记的内角的对边分别为，已知的面积为，为中点，且．
(1)若，求；
(2)若，求．
【典例11-2】（2024·山东潍坊·模拟预测）在中，内角的对边分别为，．
(1)求角；
(2)是边上的点，若，，求的值．
方向一：中线长定理
若分别为的中线，则有：
方向二：余弦和为0
在中，点为线段上一点，则有：
即．
【变式11-1】（2024·高三·江苏扬州·期中）在中，，且边上的中线AD长为1.
(1)若，求的面积；
(2)若，求的长.
【变式11-2】（2024·广东广州·模拟预测）在锐角中，角所对的边分别为，且.
(1)求角的大小；
(2)若边，边的中点为，求中线长的取值范围.
1．如图，在中，已知边上的两条中线AM，BN相交于点．
(1)求中线AM的长；
(2)求的余弦值；
(3)求面积．
重难点突破：利用正，余弦定理求解三角形中的最值或范围
【典例12-1】在中，角，，的对边分别为，，，，．
(1)求角；
(2)若是线段的中点，且，求；
(3)若为锐角三角形，求的周长的取值范围．
【典例12-2】在三角形中，内角的对边分别为，且.
(1)求；
(2)若，且，求的取值范围.
对于利用正、余弦定理解三角形中的最值与范围问题，主要有两种解决方法：一是利用基本不等式，求得最大值或最小值；二是将所求式转化为只含有三角形某一个角的三角函数形式，结合角的范围，确定所求式的范围．
【变式12-1】在中，角所对的边分别为，已知．
(1)求；
(2)若为锐角三角形，且，求面积的取值范围．
【变式12-2】（2024·高三·江苏苏州·开学考试）若△ABC中，角A，B，C所对的边分别记作a，b，c．若，，且．
(1)若，求；
(2)证明：；
(3)求的范围．
1．在锐角三角形中，分别为角所对的边，.
(1)证明：.
(2)求的范围.
考点要求
目标要求
考题统计
考情分析
正弦定理
掌握定理应用，解决三角问题
2024年II卷第15题，13分
2023年北京卷第7题，4分
2023年乙卷第4题，5分
2022年II卷第18题，12分
2025年高考数学中，解三角形问题预计仍将是考查的重点。考试将着重测试考生利用正弦定理处理三角形边角关系，以及运用正余弦定理解析平面图形边、角与面积的能力。题型上将涵盖选择、填空和解答题，其中解答题预计将占据较大比例，且多被安排在前两题位置，难度适中，属于中档题。而选择题和填空题则可能作为基础题或中档题出现，也不排除成为压轴题的可能。考生需熟练掌握相关知识，以应对多样化的题型挑战。
余弦定理
理解定理推导，应用解三角形题
2024年I卷第15题，13分
2024年甲卷第11题，5分
2022年乙卷第17题，12分
2021年乙卷第15题，5分
2021年浙江卷第14题，6分
三角形的几何计算
掌握定理，解决几何计算问题
2023年甲卷第16题，5分
2023年II卷第17题，10分
2022年天津卷第16题，15分
2021年乙卷第9题，5分
范围与最值问题
熟练方法，准确求解
2022年上海卷第19题，14分
2022年甲卷第16题，5分
2022年I卷第18题，12分