2025高考数学一轮复习-第2章-函数-第2讲 单调性与最大(小)值【课件】

这是一份2025高考数学一轮复习-第2章-函数-第2讲 单调性与最大(小)值【课件】，共45页。PPT课件主要包含了教材再现四基诊断，单调递增，单调递减，区间I，函数的最值，fx≤M，fx0＝M，fx≥M，2＋∞，－11等内容，欢迎下载使用。
课程标准　借助函数图象，会用符号语言表达函数的单调性、最大值、最小值，理解它们的作用和实际意义．
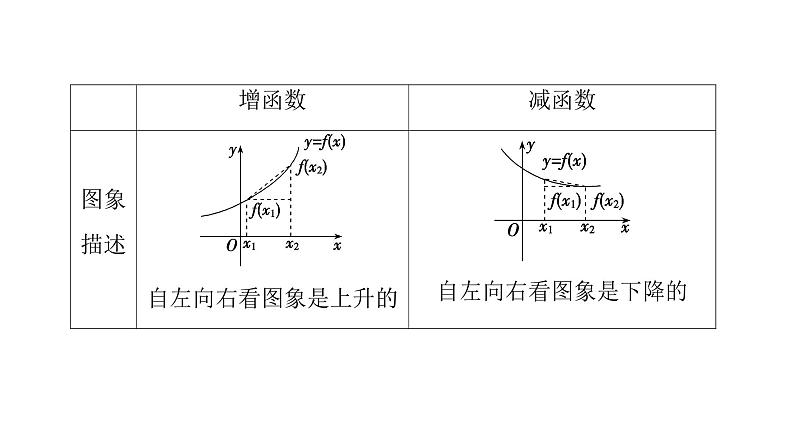
1．函数的单调性(1)函数单调性的定义
f(x1)＜f(x2)
f(x1)＞f(x2)
(2)单调区间的定义如果函数y＝f(x)在区间I上__________或__________，那么就说函数y＝f(x)在这一区间具有(严格的)单调性，________叫做y＝f(x)的单调区间．
解析：(1)错误，应对任意的x1＜x2，都有f(x1)＜f(x2)成立才可以．(2)错误，反例：f(x)＝x在[1，＋∞)上为增函数，但f(x)＝x的单调递增区间是(－∞，＋∞).(3)错误，此单调区间不能用“∪”连接，应是单调递减区间为(－∞，0)和(0，＋∞).
4．函数y＝f(x)是定义在[－2，2]上的减函数，且f(a＋1)＜f(2a)，则实数a的取值范围是__________．
确定函数的单调性(区间)
1.求函数的单调区间，应先求定义域，在定义域内求单调区间．2．(1)函数单调性的判断方法：①定义法；②图象法；③利用已知函数的单调性；④导数法．(2)函数y＝f(g(x))的单调性应根据外层函数y＝f(t)和内层函数t＝g(x)的单调性判断，遵循“同增异减”的原则．3．函数在两个不同的区间上单调性相同，一般要分开写，用“，”或“和”连接，不要用“∪”．
当x>2时，h(x)＝3－x是减函数，因此h(x)在x＝2时取得最大值h(2)＝1.
1.求函数最值的三种基本方法(1)单调性法：先确定函数的单调性，再由单调性求最值．(2)图象法：先作出函数的图象，再观察其最高点、最低点，求出最值．(3)基本不等式法：先对解析式变形，使之具备“一正二定三相等”的条件后用基本不等式求出最值．2．对于较复杂函数，可运用导数，求出在给定区间上的极值，最后结合端点值，求出最值．
比较函数值的大小时，转化到同一个单调区间内，然后利用函数的单调性解决．
角度2　解函数不等式例5　已知函数f(x)＝ln x＋2x，若f(x2－4)