2025高考数学一轮复习-第7章-立体几何与空间向量-第2讲 球及组合体【课件】

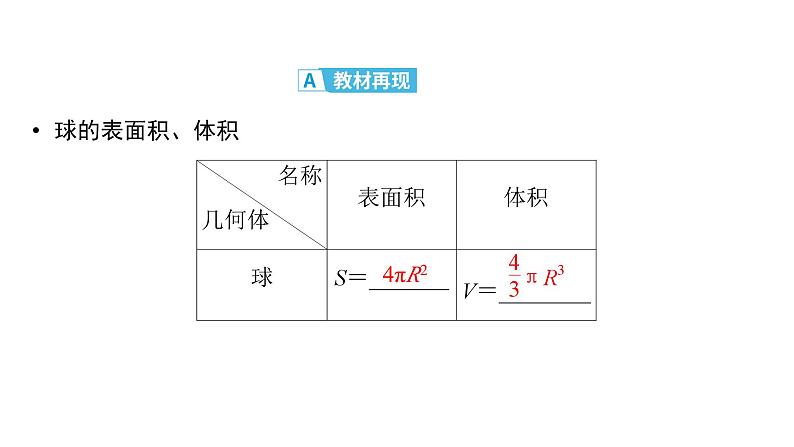
这是一份2025高考数学一轮复习-第7章-立体几何与空间向量-第2讲 球及组合体【课件】，共43页。PPT课件主要包含了教材再现四基诊断，πR2，重点串讲能力提升，球的表面积与体积，球的外接问题，球的内切问题等内容，欢迎下载使用。
课程标准　1.认识球及其简单组合体的结构特征，并能运用这些特征描述现实生活中简单物体的结构．　2.掌握球的表面积和体积的计算公式，能用公式解决简单的实际问题．　3.能解决简单的与球有关的的切、接问题．
1．判断下列结论是否正确(正确的在括号内打“√”，错误的在括号内打“×”).(1)两个球的体积之比等于它们的半径比的平方．(　　)(2)用一个平面截一个球，得到的是一个圆．(　　)解析：(1)球的体积之比等于半径比的立方，故错误．(2)用一个平面截一个球，得到的是一个圆面，故错误．
例1 (2024·浙江杭州模拟)如果两个球的体积之比为8∶27，那么这两个球的表面积之比为(　　)A．8∶27　　　　　B．2∶3C．4∶9 D．2∶9
到各个顶点距离均相等的点为外接球的球心，借助有特殊性底面的外接圆圆心，找其垂线，则球心一定在垂线上，再根据到其他顶点的距离也是半径，列关系式求解即可．
[解析]　以线段PA，PB，PC为相邻三条棱的长方体PAB′B­CA′P′C′被平面ABC所截的三棱锥P­ABC符合要求，如图，长方体PAB′B­CA′P′C′与三棱锥P­ABC有相同的外接球，其外接球的直径为长方体体对角线PP′.设外接球的半径为R，则(2R)2＝PP′2＝PA2＋PB2＋PC2＝12＋22＋32＝14，则所求球的表面积S＝4πR2＝π·(2R)2＝14π.
补形法的解题策略(1)侧面为直角三角形或正四面体，或对棱均相等的模型，可以放到正方体或长方体中去求解；(2)直三棱锥补成三棱柱求解．
与球截面有关的解题策略(1)定球心：如果是内切球，球心到切点的距离相等且为半径；如果是外接球，球心到接点的距离相等且为半径；(2)作截面：选准最佳角度作出截面，达到空间问题平面化的目的．
已知A，B，C为球O的球面上的三个点，⊙O1为△ABC的外接圆．若⊙O1的面积为4π，AB＝BC＝AC＝OO1，则球O的表面积为(　　)A．64π B．48πC．36π D．32π
“切”的问题处理规律(1)找准切点，通过作过球心的截面来解决．(2)体积分割是求内切球半径的常用方法．
(2024·江苏南京调研)已知正方形ABCD的边长为2，E为边AB的中点，F为边BC的中点，将△AED，△DCF，△BEF分别沿DE，DF，EF折起，使A，B，C三点重合于点P，则三棱锥P­DEF的外接球与内切球的表面积比值为(　　)A．6 B．12C．24 D．30