2025高考数学一轮复习-第7章-立体几何与空间向量-第7讲 利用空间向量研究直线、平面间的位置关系【课件】

这是一份2025高考数学一轮复习-第7章-立体几何与空间向量-第7讲 利用空间向量研究直线、平面间的位置关系【课件】，共60页。PPT课件主要包含了教材再现四基诊断，平行或重合，u1·u2＝0，u·n＝0，n1·n2＝0，α⊥β，α∥β，重点串讲能力提升，①②③等内容，欢迎下载使用。
课程标准　1.理解直线的方向向量及平面的法向量，能用向量方法证明立体几何中有关线面位置关系的一些简单定理．　2.能用向量语言表述线线、线面、面面的平行和垂直关系．
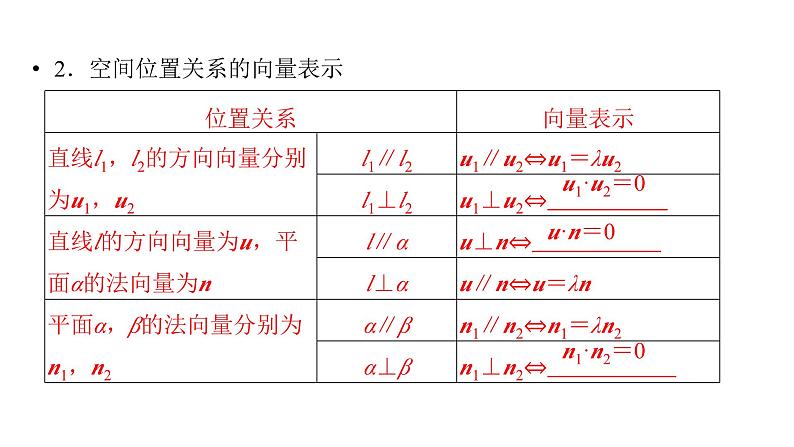
1．直线的方向向量和平面的法向量(1)直线的方向向量：如果表示非零向量a的有向线段所在直线与直线l_____________，则称此向量a为直线l的方向向量．(2)平面的法向量：直线l⊥α，取直线l的方向向量a，则向量a叫做平面α的法向量．
2．空间位置关系的向量表示
3.利用空间向量解决立体几何问题的一般步骤(1)观察图形，建立恰当的空间直角坐标系；(2)写出相应点的坐标，求出相应直线的方向向量；(3)设出相应平面的法向量，利用两直线垂直，其相应方向向量数量积为零列出方程组求出法向量；(4)将空间位置关系转化为向量关系；(5)根据定理结论求解．
1．判断下列结论是否正确(正确的在括号内打“√”，错误的在括号内打“×”).(1)直线的方向向量是唯一确定的．(　　)(2)若直线a的方向向量和平面α的法向量平行，则a∥α.(　　)(3)若{a，b，c}是空间的一个基底，则a，b，c中至多有一个零向量．(　　)(4)在空间直角坐标系中，在yOz平面上的点的坐标一定是(0，b，c).(　　)
解析：(1)直线的方向向量不是唯一的，有无数多个．(2)a⊥α.(3)若a，b，c中有一个是0，则a，b，c共面，不能构成空间一个基底．
2．已知向量m是直线l的方向向量，向量n是平面α的法向量，则“m⊥n”是“l∥α”的(　　)A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件解析：由l∥α，得m⊥n，所以“m⊥n”是“l∥α”的必要条件；而由m⊥n不一定有l∥α，也可能l⊂α，故“m⊥n”不是“l∥α”的充分条件．
4．设u，v分别是两个不同平面α，β的法向量，u＝(－2，2，5)，当v＝(3，－2，2)时，α与β的位置关系为________；当v＝(4，－4，－10)时，α与β的位置关系为________．解析：当v＝(3，－2，2)时，u·v＝－2×3＋2×(－2)＋5×2＝0，u⊥v，所以α⊥β；当v＝(4，－4，－10)时，v＝－2u，u∥v，所以α∥β.
直线的方向向量与平面的法向量
1.若平面α与β的法向量分别是a＝(2，4，－3)，b＝(－1，2，2)，则平面α与β的位置关系是(　　)A．平行 B．垂直C．相交但不垂直 D．无法确定解析：因为a·b＝(2，4，－3)·(－1，2，2)＝0，所以a⊥b，所以平面α⊥β.
2．设直线l1，l2的方向向量分别为a＝(－2，2，1)，b＝(3，－2，m).若l1⊥l2，则m＝________．解析：∵l1⊥l2，∴a⊥b，∴a·b＝－6－4＋m＝0，∴m＝10.
利用空间向量证明平行问题
1.利用向量法证明平行问题的类型及常用方法(1)线线平行：方向向量平行．(2)线面平行：平面外的直线的方向向量与平面的法向量垂直．用直线的方向向量与平面的法向量垂直来证明线面平行时，仍需强调直线在平面外．(3)面面平行：两平面的法向量平行．
2．利用向量法证明(判断)平行关系，关键是建立恰当的坐标系(尽可能利用垂直条件，准确写出相关点的坐标，进而用向量表示涉及直线、平面的要素).3．向量证明的核心是利用向量的数量积或数乘向量，但向量证明仍然离不开立体几何的有关定理．
如图，在直三棱柱ABC­A1B1C1中，∠ABC＝90°，BC＝2，CC1＝4，点E在线段BB1上，且EB1＝1，D，F，G分别为CC1，C1B1，C1A1的中点．求证：平面EGF∥平面ABD.
利用空间向量证明垂直问题
例3　如图所示，已知四棱锥P­ABCD的底面是直角梯形，∠ABC＝∠BCD＝90°，AB＝BC＝PB＝PC＝2CD，平面PBC⊥底面ABCD.求证：(1)PA⊥BD；(2)平面PAD⊥平面PAB.
[证明]　(1)取BC的中点O，连接PO.∵△PBC为等边三角形，∴PO⊥BC.∵平面PBC⊥底面ABCD，平面PBC∩底面ABCD＝BC，PO⊂平面PBC，∴PO⊥底面ABCD.以BC的中点O为坐标原点，以BC所在直线为x轴，过点O与AB平行的直线为y轴，OP所在直线为z轴，建立空间直角坐标系，如图所示．
又∵PA∩PB＝P，PA⊂平面PAB，PB⊂平面PAB，∴DM⊥平面PAB.∵DM⊂平面PAD，∴平面PAD⊥平面PAB.
利用向量法证明垂直问题的类型及常用方法(1)线线垂直：证明两直线的方向向量垂直，即证明它们的数量积为零；(2)线面垂直：直线的方向向量与平面的法向量共线，或利用线面垂直的判定定理转化为证明线线垂直；(3)面面垂直问题：两个平面的法向量垂直，或利用面面垂直的判定定理转化为证明线面垂直．
与平行、垂直有关的探索性问题
探索性问题通常分为两类：一类是已知点存在，求点的位置；一类是判断点的“存在性”问题．其中，在点的“存在性”问题中，先假设所求点存在，将其作为已知条件，得出点的位置或与题设条件矛盾的结论，从而得到结果．在设参数求解点的坐标时，若出现多解的情况，则应分析不同解的含义，判断哪些解是符合题设条件的，再做出取舍．
(2024·河北石家庄质检)如图，棱柱ABCD­A1B1C1D1的所有棱长都等于2，∠ABC和∠A1AC均为60°，平面AA1C1C⊥平面ABCD.(1)求证：BD⊥AA1.(2)在直线CC1上是否存在点P，使BP∥平面DA1C1？若存在，求出点P的位置，若不存在，请说明理由．
角度2　有关垂直的探索例5　如图，四边形ABCD和三角形ADE所在平面互相垂直，AB∥CD，AB⊥BC，∠DAB＝60°，AB＝AD＝4，AE⊥DE，AE＝DE，平面ABFE与平面CDEF交于EF.(1)求证：CD∥EF.(2)在线段BC上是否存在点M，使AM⊥EM？若存在，求出BM的长；若不存在，请说明理由．
(1)[证明]　在四边形ABCD中，AB∥CD.因为AB⊂平面ABFE，CD⊄平面ABFE，所以CD∥平面ABFE.因为CD⊂平面CDEF，且平面ABFE∩平面CDEF＝EF，所以CD∥EF.
(2)[解]　线段BC上不存在点M，使AM⊥EM.理由如下：如图，取AD的中点N，连接BN，EN.在等腰直角△ADE中，EN⊥AN.因为平面ADE⊥平面ABCD，交线为AD，且EN⊂平面ADE，所以EN⊥平面ABCD.又BN⊂平面ABCD，所以EN⊥BN.由题意得AN⊥BN.如图，建立空间直角坐标系N­xyz，
对于存在判断型问题的求解，应先假设存在，把要成立的结论当作条件，据此列方程或方程组，把“是否存在”问题转化为“点的坐标是否有解，是否有规定范围内的解”等．
(2024·山东聊城模拟)如图，在正四棱柱ABCD­A1B1C1D1中，AA1＝2AB＝2，E，F分别为棱AA1，CC1的中点，G为棱DD1上的动点．(1)求证：B，E，D1，F四点共面．(2)是否存在点G，使得平面GEF⊥平面BEF？若存在，求出DG的长度；若不存在，请说明理由．
(1)证明：如图所示，连接D1E，D1F，取BB1的中点为M，连接MC1，ME.因为E为AA1的中点，所以EM∥A1B1∥C1D1，且EM＝A1B1＝C1D1，所以四边形EMC1D1为平行四边形，所以D1E∥MC1.又因为F为CC1的中点，所以BM∥C1F，且BM＝C1F，所以四边形BMC1F为平行四边形，所以BF∥MC1，所以BF∥D1E，所以B，E，D1，F四点共面．