安徽省皖江名校2024-2025学年高一上学期12月联考数学试卷(含答案)

这是一份安徽省皖江名校2024-2025学年高一上学期12月联考数学试卷(含答案)，共13页。试卷主要包含了选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题
1．若集合，，则( )
A.B.C.D.
2．命题p：“”的否定是( )
A.，B.
C.，D.，
3．计算( )
A.14B.49C.D.
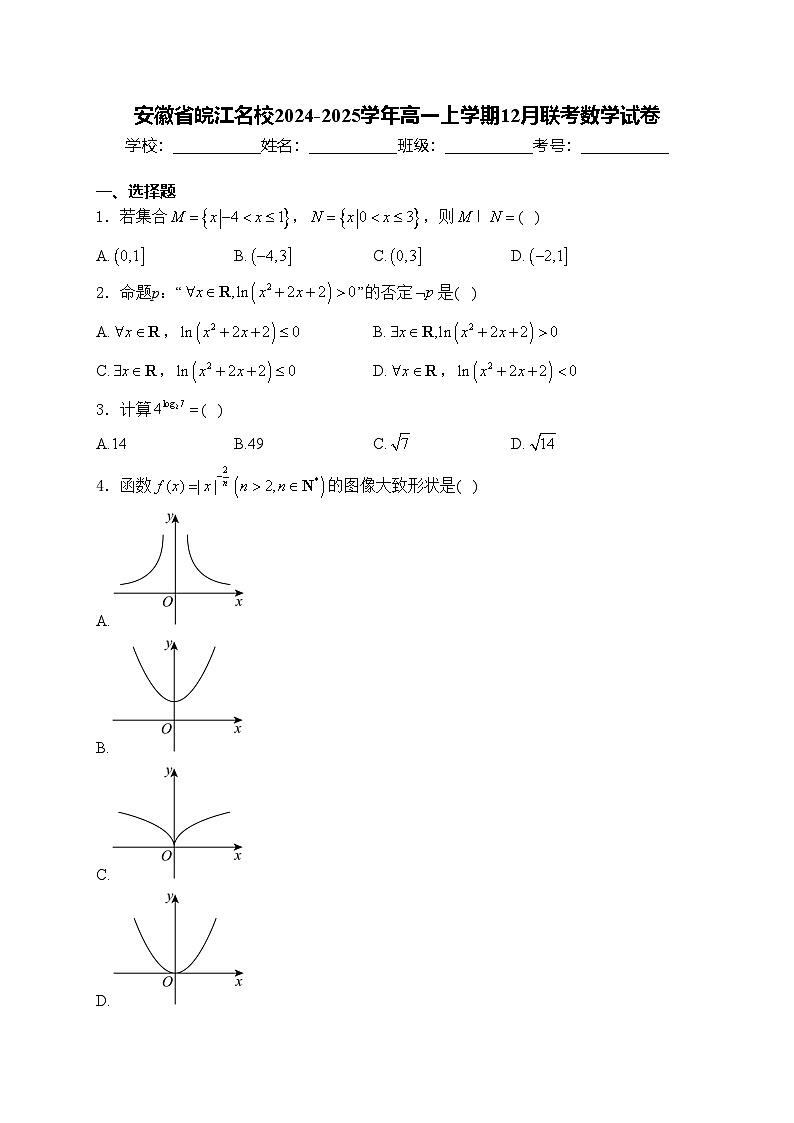
4．函数的图像大致形状是( )
A.
B.
C.
D.
5．设，若函数在上的最小值是2，则其在上的最大值是( )
A.3B.4C.5D.6
6．设，则“”是“关于x的方程有两个负实根”的( )
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件
7．下列四个数中最大的是( )
A.B.C.D.
8．已知函数若函数在区间内有且仅有两个零点，则实数t的取值范围是( )
A.B.C.D.
二、多项选择题
9．下列命题中正确的是( )
A.“”是“”的充分不必要条件
B.“”是“”的必要不充分条件
C.“”是“”的既不充分也不必要条件
D.“”是“”的充要条件
10．下列几个不等式中，能取到等号的是( )
A.B.
C.D.
11．设，，下列四个命题中，正确的是( )
A.当时的单调递增区间是和
B.当时的图像与直线有两个交点
C.在内单调递减的充要条件是
D.若的最小值是零，则
三、填空题
12．已知幂函数的图像过点，则其解析式___________.
13．设方程的两根是，，若不等式的解集是，则的值是___________.
14．若正数a，b满足，则的最大值是___________.
四、解答题
15．已知命题.
(1)若不等式的解集是，求a的值；
(2)若p是q的充分不必要条件，求实数a的取值范围
16．某医院为改善医疗技术，2024年初以72万元的价格购进一套医疗设备已知该套医疗设备每年获得的总收入为40万元，使用年后所需要的各种维护费用总计为万元，2024年为第一年
(1)写出该套医疗设备的利润函数的表达式，并求的最大值；
(2)第几年后，该套医疗设备的年平均利润最大？
17．一般地，我们把形如的函数称为飘带函数，若飘带函数在上的最小值、最大值分别为和1.
(1)确定a，b的值；
(2)求的零点
18．定义在上的函数满足：①当时，；②对任意实数x，y都有.
(1)证明：当时，；
(2)判断在上的单调性；
(3)解不等.
19．我们知道，若，则有不等式成立（当且仅当时等号成立）从可以得到即正数a，b，c的算术平均数的平方不大于a，b，c平方的算术平均数请运用这个结论解答下列三道题：
(1)求代数式的最大值；
(2)已知，，若不等式恒成立，求实数m的取值范围；
(3)若a，b，，证明：.
参考答案
1．答案：A
解析：因为，，
所以，
故选：A
2．答案：C
解析：“”改为“”，“”改为“”，
因此是“，”.
故选：C.
3．答案：B
解析：因为.
故选：B.
4．答案：A
解析：由题设易知，而时，
幂函数在第一象限单调递减
故选：A
5．答案：A
解析：设，
则.
因为，所以，
当时，；
当时，.
故选：A.
6．答案：D
解析：方程的判别式，
当时，的符号可正可负，
即由推不出方程有两个负实根
反之，若方程有两个负实根，
则，且，
因此由不能推出.
所以“”是“方程有两个负实根”的既不充分也不必要条件
故选：D.
7．答案：C
解析：因为，
所以，
因为，
所以，
所以最大,
故选：C.
8．答案：C
解析：函数在区间内有且仅有两个零点，
等价于在区间内有且仅有两个实数根，
又等价于函数的图像与直线在区间内有且仅有两个公共点，
因为，
由图知，
即，解得.
故选：C.
9．答案：AD
解析：由，所以，若，
例如，则得不到，故A正确；
由，则，若，
例如，，则没意义，
故“”是“”充分不必要条件，故B错误；
若“”则“”，反过来若，
例如，则，
故“”是“”的充分不必要条件，故B错误；
由，则，
反过来若则，
故“”是“”的充要条件，故D正确；
故选：AD.
10．答案：ABC
解析：对A，
，当且仅当时等号成立；
对B，∵，∴，
，
当且仅当时等号成立；
对C，∵，则，
所以，，
则，当且仅当时等号成立；
对D，∵，∴，
当且仅当，即时等号成立，
而，
因此中的等号取不到
故选：ABC.
11．答案：AC
解析：对于A，当时，二次函数与x轴交于点和，
画出函数的图像如下：
的单增区间是和，故A正确；
对于B，当时，二次函数与x轴交于点和，
顶点是，
画出函数的图像如下：
的图像与直线有三个交点，故B不正确；
对于C，当时，在内单调递减；
当时，在内单减，故C正确
对于D，若的最小值是零，
则，，均可以，故D不正确
故选：AC.
12．答案：
解析：设，则，解得.
故答案为：.
13．答案：19
解析：由不等式的解集是
可知：的两根为-3，2，
所以，
所以，
所以就是，，
于是.
故答案为：19.
14．答案：
解析：因为对任意实数x，y都有，
当且仅当时等号成立，
所以，
当且仅当，
即，时等号成立
故的最大值是.
故答案为：.
15．答案：(1)
(2)
解析：(1)由题意知，-3，-2是方程的两根，
所以，且，解得.
(2)因为，
即，所以.
因为p是q的充分不必要条件，
所以集合是集合的真子集
因此，解得.
故实数a的取值范围是.
16．答案：(1)，最大值56
(2)第6后年平均利润最大
解析：(1)，
因为，
所以当时，取最大值56.
(2)年平均利润为
，
当且仅当，即时取等号，
故第6后年平均利润最大
17．答案：(1)，或，
(2)和或和
解析：(1)当，时，是上的增函数，
所以，即，解得；
当，时，是上的减函数，
所以，即，解得；
故，或，
(2)当，时，，令，
所以的两个零点分别是和；
当，时，，令，
所以的两个零点分别是和；
故的零点为和或和.
18．答案：(1)证明见解析
(2)增函数
(3)
解析：(1)令，则，所以
当时，，则.
在中，
令，则，所以
(2)设，则，所以.
于是，
故在上是增函数
(3)由题意知，原不等式等价于
由(2)，在上是增函数得到，，
且，解得.
故原不等式的解集是.
19．答案：(1)
(2)
(3)证明见解析
解析：(1)当时，有，
即，
当且仅当，即时等号成立
而，
故代数式的最大值为.
(2)当，时，有，
所以，
即，
当且仅当时等号成立
因此的最小值为.
恒成立
恒成立.
故实数m的取值范围是.
(3)因为，
所以
，
当且仅当时等号成立
故a，b，，