中考数学专题训练：几何探究压轴题（含简单答案）

这是一份中考数学专题训练：几何探究压轴题（含简单答案），共15页。试卷主要包含了已知，实践与探究等内容，欢迎下载使用。

(1)如图1，分别取和的中点G、H，连接，那么和的数量关系是______．
(2)将图1中的绕点A旋转到图2的位置时，判断（1）中的结论是否仍然成立，并说明理由．
(3)已知正方形的边长为2，正方形的边长为10，现将正方形绕点A顺时针旋转，在整个旋转过程中，当C、P、E三点共线时，请直接写出的长．
2．实践与探究
（1）操作一：如图①，将矩形纸片对折并展开，折痕与对角线交于点E，连结，则与的数量关系为______．
（2）操作二：如图②，摆放矩形纸片与矩形纸片，使B、C、G三点在一条直线上，在边上，连结，M为的中点，连结、．求证：．
（3）拓展延伸：如图③，摆放正方形纸片与正方形纸片，使点F在边上，连结，M为的中点，连结、、．已知正方形纸片的边长为5，正方形纸片的边长为，求 的面积．
3．已知四边形，，相交于点P，且，，设，，．
(1)①如图1，当时，时，______；______；
②如图2，当时，时，______；______；
(2)观察（1）中的计算结果，利用图3证明，，三者关系．
(3)如图4，在平行四边形中，点E，F，G分别是的中点，，，，求的长．
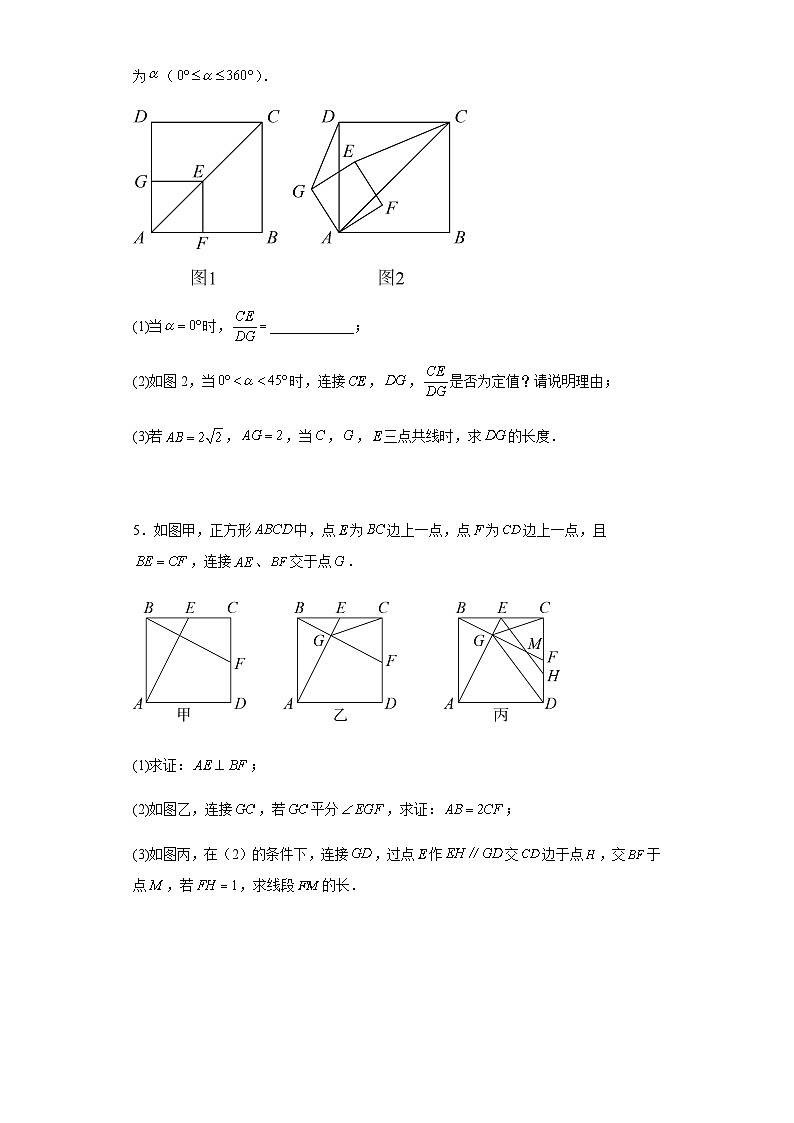
4．如图1，正方形与正方形有公共点，点，分别在，上，点在正方形的对角线上．将正方形绕点逆时针方向旋转，旋转角为（）．
(1)当时，____________；
(2)如图2，当时，连接，，是否为定值？请说明理由；
(3)若，，当，，三点共线时，求的长度．
5．如图甲，正方形中，点为边上一点，点为边上一点，且，连接、交于点．
(1)求证：；
(2)如图乙，连接，若平分，求证：；
(3)如图丙，在（2）的条件下，连接，过点作交边于点，交于点，若，求线段的长．
6．【基础巩固】（1）如图，在中，，分别在，上，，求证：．
【尝试应用】（2）如图2，在中，，，分别在，，上，四边形为平行四边 形，，，，求的长．
【拓展提高】（3）如图3，平行四边形的周长为，，分别在，上，四边形为平行四边形，，，求EF的长．
7．如图1，已知正方形中，为对角线，边长为3，为边上一点，过点作于点，．
(1)如图1，连结，求线段的长．
(2)保持不动，将正方形绕点旋转至如图2的位置，连结，点为的中点，连接、，探求与关系，并证明你的结论；
(3)保持不动，将正方形绕点旋转一周，求出的中点在这个过程中的运动路径长及的最小值．
8．如图，在矩形中，点E为边的中点，点F为上的一个动点，连接并延长，交的延长线于点G，以为底边在下方作等腰，且．
(1)如图①，若点H恰好落在上，连接，．
①求证：；
②若，，求的面积；
(2)如图②，点H落在矩形内，连接，若，，求四边形面积的最大值．
9．在菱形中，，点是射线上一动点，以为边向右侧作等边，点的位置随着点的位置变化而变化．
(1)如图1，当点在菱形内部或边上时，连接，与的数量关系是______，与的位置关系是______；
(2)当点在菱形外部时，（1）中的结论是否还成立？若成立，请予以证明；若不成立，请说明理由（参照图3的情况予以证明）
(3)如图4，当点在线段的延长线上时，连接，若，，求四边形的面积．
10．在矩形中，，，将矩形绕点B顺时针旋转得到矩形，A，C，D的对应点分别为，，．
(1)当点落在线段上时，完成以下探究．
①如图1，求的长．
②如图2，延长交于点E，求证：．
(2)如图3，以为斜边在右侧作等腰直角三角形，，交于点G，交于点H，若，求的长．
(3)如图4，矩形的对角线与相交于点P，连接，，则面积的最小值为___．
11．在正方形中，E是边上一点（点E不与点B，C重合），，垂足为点E，与正方形的外角的平分线交于点F．
(1)如图1，若点E是的中点，猜想与的数量关系是______；证明此猜想时，可取的中点P，连接．根据此图形易证．则判断的依据是_________
(2)点E在边上运动．
①如图2，（1）中的猜想是否仍然成立?请说明理由．
②如图3，连接，若正方形的边长为1，直接写出的周长c的取值范围．
12．如图，在中， ，，点D为直线右上方一点，且满足，连接．
(1)如图1，若，交于点O，求的长；
(2)如图2，点E为线段上一点，连接、，且满足，试证明；
(3)如图3，在（2）的条件下，以，为边构造平行四边形，当时，直接写出的面积．
13．如图1，中，，，，点P、Q是边，上两个动点，且，以，为邻边作平行四边形，，分别交于点E，F，设．
(1)当平行四边形的面积为时，求m的值；
(2)求证：；
(3)如图2，连接，，，当与的一边平行时，求的面积．
14．如图1，在矩形中，，，E是边上的一点，连接，将矩形沿折叠，顶点D恰好落在边上的点F处，延长交的延长线于点G．
(1)求线段的长：
(2)求证：四边形为菱形；
(3)如图2，M，N分别是线段上的动点（与端点不重合），且，设，是否存在这样的点N，使是直角三角形？若存在，请求出x的值；若不存在，请说明理由．
15．如图，点E，F分别在正方形的边，上，且，点P在射线上（点P不与点F重合）．将线段绕点E顺时针旋转得到线段，过点E作的垂线，垂足为点H，交射线于点Q．
(1)如图1，若点E是的中点，点P在线段上，请直接写出线段，，满足的数量关系______．
(2)如图2，若点E不是的中点，点P在线段上，判断（1）中的结论是否仍然成立，若成立，请写出证明过程；若不成立，请说明理由．
(3)正方形的边长为9，，，请直接写出线段的长______．
16．（1）如图①，在正方形中，点E、F分别为，边上的点，且满足，连接．将绕点A顺时针旋转得到，易证，从而得到结论：，根据这个结论，若正方形的边长为2，则的周长为______．
（2）如图②，若在四边形中，，，E、F分别是、上的点，且，试猜想，，之间有何数量关系，证明你的结论．
（3）如图③，四边形中，，，E、F分别是边、延长线上的点，且，试探究线段，，之间的数量关系，请直接写出你的猜想（不必说明提由）．
17．在菱形中，，，点E是对角线上的一动点，以为边向右作等边三角形，连结．
(1)如图①，当点F在菱形内部时，求证：．
(2)如图②，当C、E、F三点在一条直线上时，___________．
(3)如图③，当时，连结，四边形的面积=___________．
18．定义：有一个角是直角的平行四边形叫做矩形．
(1)根据定义判矩形
已知：如图1，在平行四边形中，是它的两条对角线，．求证：平行四边形是矩形．
(2)动手操作有发现
如图2，在矩形中，是的中点，将沿折叠后得到，点在矩形内部，延长交于点．猜想线段与有何数量关系?并证明你的结论．
(3)类比探究到一般
如图3，将(2)中的矩形改为平行四边形，其它条件不变，(2)中的结论是否仍然成立，请说明理由．
(4)解决问题巧应用
如图4，保持(2)中的条件不变，若点是的中点，且，请直接写出矩形的面积．
参考答案：
1．(1)
(2)依然成立．
(3)或
2．（1）（3）
3．(1)①，；②，
(2)，
(3)
4．(1)
(3)或者
5．(3)
6．（2）；（3）
7．(1)
(2)且
(3)的运动路径长为，的最小值为
8．(1)②10；
(2)．
9．(1)，
(2)成立，
(3)
10．(1)①；
(2)
(3)9
11．(1)，
(2)①成立；②
12．(1)
(3)
13．(1)m的值是1
(3)的面积为或
14．(1)
(3)存在，或
15．(1)
(2)成立
(3)4或8
16．（1）4；（2），（3）．
17．(2)2
(3)
18．(2)
(3)成立，
(4)