2024-2025学年江西省南昌市高一上学期第二次月考数学检测试题（附解析）

这是一份2024-2025学年江西省南昌市高一上学期第二次月考数学检测试题（附解析），共13页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
一、单选题（本大题共8小题）
1．若全集，集合，则 （ ）
A．B．
C．D．
2．命题“，”的否定为（ ）
A．，B．，
C．，D．，
3．幂函数在上是增函数，则实数的值为（ ）
A．2或B．C．2D．或
4．若函数，则的值为（ ）
A．1B．C．D．
5．函数的图象大致为（ ）
A． B．
C． D．
6．若偶函数满足，恒成立，则（ ）
A．B．
C．D．
7．已知关于的函数在上单调递增，则实数的取值范围是（ ）
A．B．C．D．
8．已知函数为偶函数，为奇函数，且当时，，则（ ）
A．2B．C．1D．
二、多选题（本大题共3小题）
9．下列说法正确的是（ ）
A．与表示同一个函数
B．函数的定义域为，则函数的定义域为
C．已知，则的最小值为
D．函数的值域为
10．环境污染已经触目惊心，环境质量已经成为“十三五”实现全面建成小康社会奋斗目标的短板和瓶颈．南昌某化工厂每一天中污水污染指数与时刻（时）的函数关系为其中为污水治理调节参数，且规定每天中的最大值作为当天的污水污染指数，则使该厂每天的污水污染指数不超过的的取值可以为（ ）
A．B．C．D．
11．用表示不超过的最大整数，例如，.已知，则（ ）
A．
B．为奇函数
C．为上的增函数
D．与图象所有交点的横坐标之和为
三、填空题（本大题共3小题）
12．设，若，则 ．
13．已知，若命题：“存在，使得”为假命题，则的最小值为 .
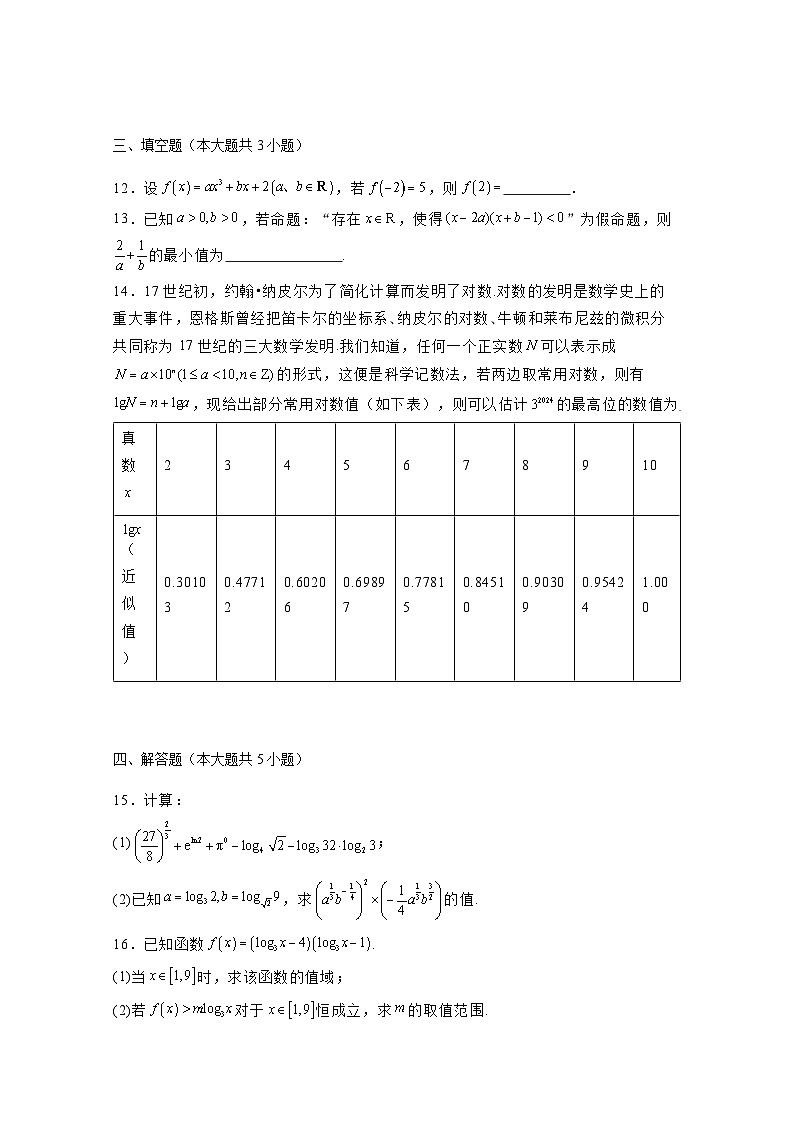
14．17世纪初，约翰•纳皮尔为了简化计算而发明了对数.对数的发明是数学史上的重大事件，恩格斯曾经把笛卡尔的坐标系､纳皮尔的对数､牛顿和莱布尼兹的微积分共同称为17世纪的三大数学发明.我们知道，任何一个正实数可以表示成的形式，这便是科学记数法，若两边取常用对数，则有，现给出部分常用对数值（如下表），则可以估计的最高位的数值为
四、解答题（本大题共5小题）
15．计算：
(1)；
(2)已知，求的值.
16．已知函数.
(1)当时，求该函数的值域；
(2)若对于恒成立，求的取值范围.
17．已知定义在上的函数图象关于原点对称，且．
(1)求的解析式
(2)判断并用定义证明的单调性；
(3)解不等式．
18．已知为上的奇函数，为上的偶函数，且．
(1)分别求函数，的解析式；
(2)设，，对任意的，总存在，使得，求实数的取值范围．
19．若函数满足：对任意正数，都有，则称函数为“函数”．
(1)试判断函数是否为“函数”，并说明理由；
(2)若函数是“函数”，求实数a的取值范围；
(3)若函数为“函数”，，对任意正数，都有，，证明：对任意，都有．
答案
1．【正确答案】A
【详解】解：因为，，
所以，
所以.
故选：A.
2．【正确答案】D
【详解】命题“，”的否定为：“，”.
故选：D.
3．【正确答案】C
【详解】由题意得，，解得.
故选：C.
4．【正确答案】C
【详解】因为，
所以，
则.
故选：C.
5．【正确答案】A
【分析】根据函数的奇偶性和单调性即可判断选项.
【详解】设，
对任意，，
所以，
所以的定义域为，
，
所以函数为奇函数.
令，
可得，即，
所以，可得，
由可得，解得，
所以的定义域为，
又，
所以函数为奇函数，排除BD选项，
当时，是减函数，
则，，
所以，排除C选项.
故选A.
6．【正确答案】A
【详解】由，恒成立，
可得在上单调递增，
又为偶函数，故，
由，，
故，故.
故选：A.
7．【正确答案】B
【详解】令，
则，因为，所以在上单调递减，
而在上单调递增，
由复合函数的单调性可知，在单调递减，且，
所以，则，所以.
故选：B.
8．【正确答案】A
【详解】由为偶函数，则有，
由为奇函数，则有，即，
则.
故选：A.
9．【正确答案】ABD
【详解】对A：对，有，解得，即定义域为，
对，有，解得，即定义域为，
又，故与表示同一个函数，故A正确；
对B：函数的定义域为，则有，
故，解得，故函数的定义域为，故B正确；
对C：由，则，则，
令，由函数在上单调递增，
故，故C错误；
对D：令，则，
故，
当且仅当时，等号成立，故函数的值域为，故D正确.
故选：ABD.
10．【正确答案】AB
【详解】设，则当时，.
可得，
则，
显然在上是减函数，在上是增函数，
则，且,
则有，解得，
又，故调节参数应控制在内，
结合选项可知：AB正确，CD错误；
故选：AB.
11．【正确答案】ACD
【详解】对A：，故A正确；
对B：由，，
故不为奇函数，故B错误；
对C：令，则，
由，则，故，
故为R上的增函数，故C正确；
对D：令，即，
又，所以，可得，
当时，有，，即为图象交点的横坐标；
当时，，则，解得，即为图象交点的横坐标；
当时，，则，故不为图象交点的横坐标；
当时，，则，解得，即为图象交点的横坐标；
综上，图象所有交点的横坐标之和为，故D正确.
故选：ACD.
12．【正确答案】
【详解】由题意可知，，
即，又，
所以.
故答案为.
13．【正确答案】
【详解】因为命题：“存在，使得”为假命题，
则“任意，都有”为真命题，
对于，所以，
要使“任意，都有”为真命题，
则，即，
因为，
所以，
当且仅当，即时，等号成立.
所以的最小值为.
故答案为.
14．【正确答案】
【详解】依题意，设，则，
因为，
所以，
由表格可知，，
所以的最高位的数值为.
故答案为.
15．【正确答案】(1)
(2)
【详解】（1）
.
（2）因为，，
所以
.
16．【正确答案】(1)
(2)
【详解】（1）令，当时，，
，
由函数在上单调递减，
则， ，
故当时，求该函数的值域为；
（2）由可得，
即对于恒成立，
当时，，恒成立；
当时，，
又在上单调递减，故，
故，即；
综上所述.
17．【正确答案】(1)，
(2)在上单调递减，证明见解析
(3)
【详解】（1）由题意可得，即，
又，故，
即，此时有，
故关于原点对称，故，；
（2）在上单调递减；证明如下：
令，则
，
由，则，，，
故，即在上单调递减；
（3）由题意可得为奇函数，则有，
又在上单调递减，则有，解得.
18．【正确答案】(1)，
(2)
【详解】（1）由，则，
由为上的奇函数，为上的偶函数，
则有，，
故，
即，
即，
则；
（2）由题意可得在上的值域为在上的值域的子集，
，
令，则在上单调递增，故当时，
故时，；
当，，
则当时，在上单调递增，故，
则有，解得；
当时，在上单调递减，故，
则有，无解；
当时，，，
则有，解得；
综上所述.
19．【正确答案】(1)函数不是“函数”，理由见解析
(2)
(3)证明见解析
【详解】（1）对于fx=lnx，取，
则，．
因为，不满足，
故fx=lnx不是“函数”；
（2）因为函数是“函数”，
所以对于任意的，
有恒成立，
即恒成立，
所以恒成立，
又，故，
则，
则，即，即实数的取值范围为
（3）由函数为“函数”，可知对于任意正数，
都有，，且，
令，可知，即，
故对于自然数与正数，
都有，
对任意，可得，又，
所以，
同理，
故，
即.真数
2
3
4
5
6
7
8
9
10
（近似值）
0.30103
0.47712
0.60206
0.69897
0.77815
0.84510
0.90309
0.95424
1.000