2024-2025学年山东省青岛市高二上学期期中考试数学检测试卷（附解析）

这是一份2024-2025学年山东省青岛市高二上学期期中考试数学检测试卷（附解析），共15页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
一、单选题（本大题共8小题）
1．设直线：的倾斜角为，则的值为（ ）
A．2B．C．D．
2．已知直线平分圆的周长，则（ ）
A．2B．1C．D．4
3．已知直线的一个方向向量为，平面的一个法向量为，若，则（ ）
A．1B．2C．3D．4
4．在四面体中，，若，则（ ）
A．B．C．D．
5．已知椭圆：（）的离心率为，且点为椭圆的一个焦点，则椭圆与直线在第一象限的交点为（ ）
A．B．C．D．
6．圆：与圆：的公切线的条数为（ ）
A．1B．2C．3D．4
7．若双曲线的右焦点到其渐近线的距离为，则双曲线的离心率为（ ）
A．B．C．D．
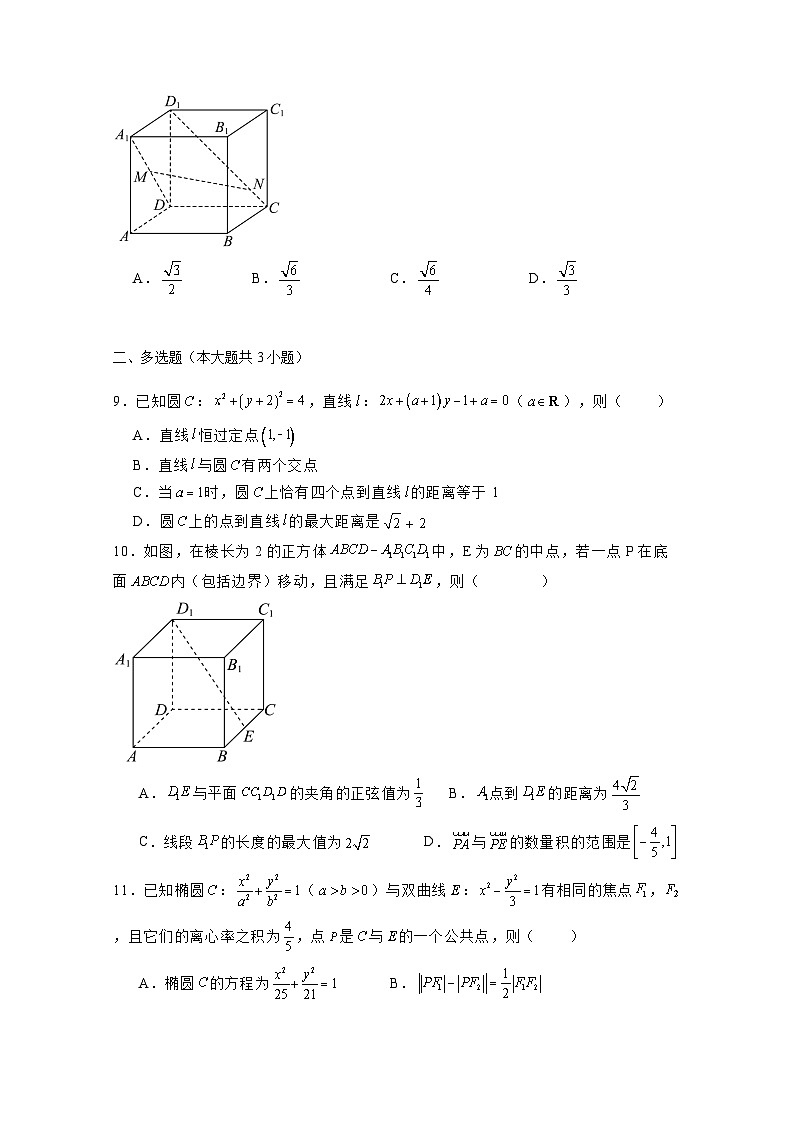
8．如图，在棱长为2的正方体中，为线段的中点，为线段上的动点，则直线与直线所成角的余弦值的最大值为（ ）

A．B．C．D．
二、多选题（本大题共3小题）
9．已知圆：，直线：（），则（ ）
A．直线恒过定点
B．直线与圆有两个交点
C．当时，圆上恰有四个点到直线的距离等于1
D．圆上的点到直线的最大距离是
10．如图，在棱长为2的正方体中，E为的中点，若一点P在底面内（包括边界）移动，且满足，则（ ）
A．与平面的夹角的正弦值为B．点到的距离为
C．线段的长度的最大值为 D．与的数量积的范围是
11．已知椭圆：（）与双曲线：有相同的焦点，，且它们的离心率之积为，点是与的一个公共点，则（ ）
A．椭圆的方程为B．
C．为等腰三角形D．对于上的任意一点，
三、填空题（本大题共3小题）
12．在空间直角坐标系中，点，点，点，则在方向上的投影向量的坐标为 ．
13．如图，赵州桥是一座位于河北省石家庄市赵县城南洨河之上的石拱桥，因赵县古称赵州而得名．赵州桥始建于隋代，是世界上现存年代最久远、跨度最大、保存最完整的单孔石拱桥．小明家附近的一座桥是仿赵州桥建造的抛物线形拱桥．这座桥的拱顶离水面时，水面宽，当水面的宽度为时，水面下降了 ．
14．已知点是圆：上的动点，点，则线段的中点的轨迹方程是 ；若直线：，为直线上的动点，过点作点的轨迹的切线，切点为，，设，当四边形的面积最小时，面积为 ．
四、解答题（本大题共5小题）
15．已知的顶点，顶点在轴上，边上的高所在的直线方程为边上的中线所在的直线方程为.
(1)求直线的方程；
(2)求的值.
16．如图，在六棱柱中，底面是正六边形，设，，.

(1)用，，分别表示，．
(2)若，，，求：
（ⅰ）；
（ⅱ）．
17．已知抛物线：的焦点为．
(1)求抛物线的焦点坐标和准线方程；
(2)过焦点的直线与抛物线交于，两点，若，求线段的长．
18．已知直线：，圆：．
(1)当为何值时，直线被圆截得的弦最长？当为何值时，直线被圆截得的弦最短？
(2)是否存在，使得直线被圆截得的弦长为？若存在，求出的值；若不存在，请说明理由．
19．已知椭圆：（）的焦距为，，分别为椭圆的左、右焦点，过的直线与椭圆交于两点，的周长为8.
(1)求椭圆的标准方程.
(2)对于，是否存在实数，使得直线分别交椭圆于点，且？若存在，求出的值；若不存在，请说明理由.
答案
1．【正确答案】C
【详解】直线：可化为，
所以直线的斜率为，即 ，
故选:C.
2．【正确答案】B
【详解】因为直线平分圆的周长，
所以直线过圆心，
所以，解得，
故选:B.
3．【正确答案】B
【详解】由即可得，解得；
故选：B
4．【正确答案】A
【详解】如图，

因为，所以，又，
所以，
又，
所以且，解得：．
故选：A
5．【正确答案】D
【详解】由题可得，，解得，
所以椭圆方程为，
联立，可得，解得，
所以椭圆与直线在第一象限的交点为，
故选:D.
6．【正确答案】C
【详解】由，可得，
所以圆心，
设两圆的半径分别为，则，
圆心距，
所以两圆外切，则公切线的条数为3条，
故选:C.
7．【正确答案】B
【详解】根据对称性，双曲线的焦点到两条渐近线的距离相等，
其中一条渐近线的方程为，即，
右焦点Fc,0到的距离等于，
所以，所以，
即，则，所以，
故选：B.
8．【正确答案】D
【详解】建立如图所示的空间直角坐标系，
则,0,，,2,，,0,，,0,，,0,，,2,，
设，，
则,,，
则，，
则，
设直线与直线所成角为，
则，当且仅当时取等号，
则直线与直线所成角的余弦值的最大值为，
故选：D．

9．【正确答案】ABD
【详解】
对A，由，可得，
令，解得，所以直线恒过定点，A正确；
对B，设直线直线恒过定点为，
圆心,半径，
则，
所以点在圆内，则直线与圆相交，
所以直线与圆有两个交点，B正确；
对C，时，：，即，
圆心到直线的距离，
因为，
所以圆上恰有两个点到直线的距离等于1，
且这两个点均位于圆被直线所截得的优弧上，C错误；
对D，当时，圆上的点到直线的距离有最大值，
最大值为，D正确；
故选:ABD.
10．【正确答案】ABD
【分析】建系，标点，设，根据向量垂直可得.对于A：利用空间向量求线面夹角；对于B：利用空间向量求点到线的距离；对于C：根据空间向量的模长公式分析求解；对于D：根据空间向量的数量积分析求解.
【详解】如图，以为坐标原点，分别为轴，建立空间直角坐标系，
则，设，
可得，，
若，则，可得，
则，解得，即.
对于选项A：可知平面的法向量，
则，
所以与平面的夹角的正弦值为，故A正确；
对于选项B：因为，
所以点到的距离为，故B正确；
对于选项C：因为，
则，
且，可得当且仅当时，取到最大值，
所以线段的长度的最大值为3，故C错误；
对于选项D：因为，，
则，
且，可知当时，取到最小值；
当时，取到最大值；
所以与的数量积的范围是，故D正确.
故选ABD.
11．【正确答案】ABC
【详解】
由双曲线：的方程可知，双曲线的焦点，，
离心率为，
所以椭圆的焦点为，，离心率为，
所以椭圆中，，
所以椭圆的方程为，A正确；
因为点是与的一个公共点，
所以点在双曲线上，
所以根据双曲线的定义可知，
，且，
所以，B正确；
根据对称性，不妨设，则，
又根据椭圆的定义可知，，
所以联立，解得
，所以，所以为等腰三角形，C正确；
设，则，，
所以，
解得，此时，
所以存在点的坐标为或或或，
使得，D错误；
故选：ABC.
12．【正确答案】
【详解】由题，，
所以，
，
则在方向上的投影向量的坐标为
.
故答案为: .
13．【正确答案】/
【详解】建系如图，设抛物线方程为，
则根据题意可知图中坐标为，
，，
抛物线方程为，
令，可得，
则水面下降了米
故
14．【正确答案】
【详解】
设，，则有，
根据中点坐标公式可得，，解得，
所以，整理得，
所以线段的中点的轨迹方程是；
所以可知点为圆的圆心，且
所以,
所以要使四边形的面积最小，则最小，
当时，最小，为点到直线的距离，
此时，
所以.
故答案为: ;.
15．【正确答案】(1)
(2)
【详解】（1）由边上的高所在的直线方程为，其斜率为，
则，即，又，
则，即；
（2）设，由在上，即，即，
则中点坐标为，故有，即.
16．【正确答案】(1);
(2);
【详解】（1）

如图，连接，取中点为，连接，
因为底面是正六边形，
所以,即，
所以,
又因为,
所以.
（2）由题知，，
根据，
可知，
且因为底面是正六边形，所以所以，
所以（ⅰ）
=
（ⅱ）因为，
所以
=，
所以.
17．【正确答案】(1)焦点为，准线.
(2)
【详解】（1）由抛物线方程可得，，
所以焦点为，准线.
（2）设，
根据对称性，不妨设在轴上方，则在轴下方，
根据抛物线的定义可知，，所以，
将代入可得或（舍），
所以，
所以,
所以直线的直线方程为，即，
联立，消去可得，，
根据韦达定理可得，，
所以，
所以.

18．【正确答案】(1)答案见解析；
(2)
【详解】（1）易知直线：恒过定点；
圆：的圆心为，半径；
当直线过圆心时，弦长为圆的直径，即，
解得；
当圆心与定点连线与直线垂直时，弦长最短；
此时直线的斜率为0，所以，
解得.
因此时，直线被圆截得的弦最长，时，直线被圆截得的弦最短；
（2）设圆心到直线的距离为，
由弦长为可得，解得；
即，解得
即存在，使得直线被圆截得的弦长为.
19．【正确答案】(1)
(2)存在，
【详解】（1）因为的周长为
，所以，
又因为，所以，所以，
所以椭圆的标准方程为.
（2）
设，设中点为，
联立，消去整理得，，
所以，即，
所以或，
又由韦达定理可得，，
所以，
所以，
因为，所以，
由或，可知，直线的斜率均存在，且都不等于零，
所以，即，
整理得，解得，
又因为或，所以满足题意，
所以存在.