2025年高考数学二轮复习专项精练18 空间点、直线、平面之间的位置关系（真题精练+模拟精练）

这是一份2025年高考数学二轮复习专项精练18 空间点、直线、平面之间的位置关系（真题精练+模拟精练），文件包含2025二轮复习专项精练18空间点直线平面之间的位置关系真题精练+模拟精练原卷版docx、2025二轮复习专项精练18空间点直线平面之间的位置关系真题精练+模拟精练解析版docx等2份试卷配套教学资源，其中试卷共41页， 欢迎下载使用。
【真题精练】
一、单选题
1．（2024·全国·高考真题）已知正三棱台的体积为，，，则与平面ABC所成角的正切值为（ ）
A．B．1C．2D．3
2．（2024·全国·高考真题）设为两个平面，为两条直线，且.下述四个命题：
①若，则或 ②若，则或
③若且，则 ④若与,所成的角相等，则
其中所有真命题的编号是（ ）
A．①③B．②④C．①②③D．①③④
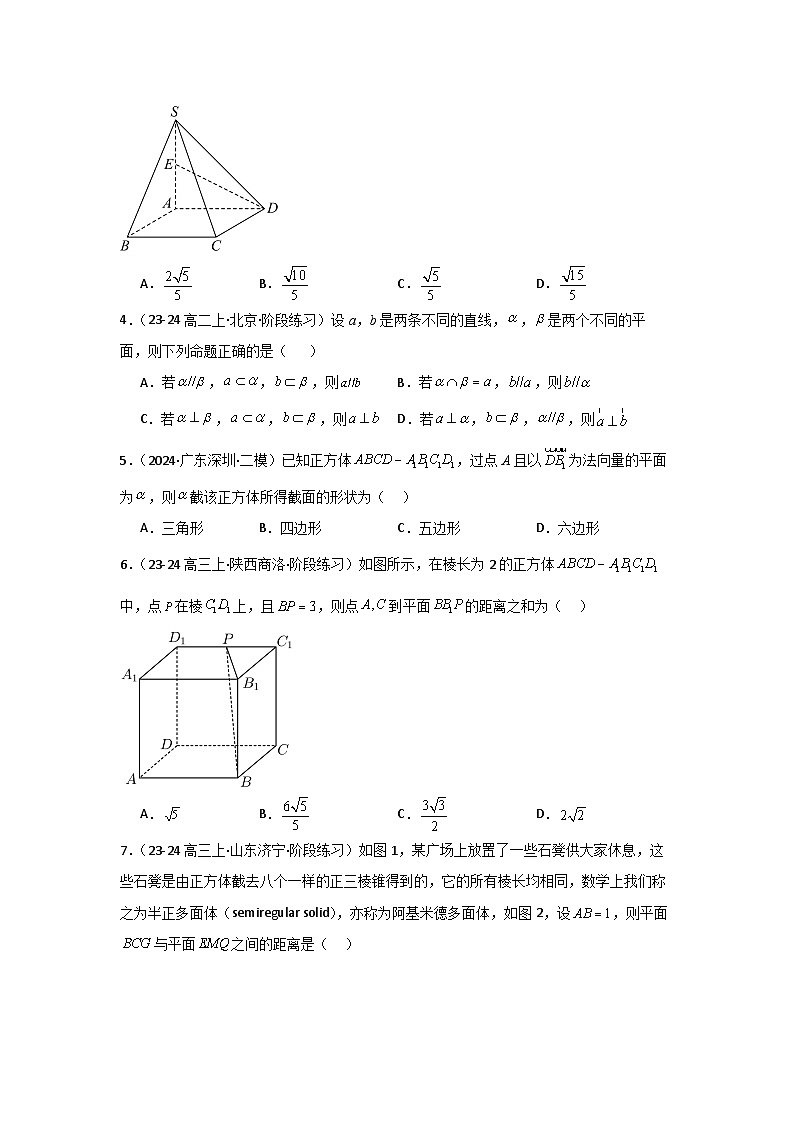
3．（2023·全国·高考真题）已知为等腰直角三角形，AB为斜边，为等边三角形，若二面角为，则直线CD与平面ABC所成角的正切值为（ ）
A．B．C．D．
4．（2023·全国·高考真题）在三棱锥中，是边长为2的等边三角形，，则该棱锥的体积为（ ）
A．1B．C．2D．3
5．（2022·全国·高考真题）在正方体中，E，F分别为的中点，则（ ）
A．平面平面B．平面平面
C．平面平面D．平面平面
6．（2022·全国·高考真题）在长方体中，已知与平面和平面所成的角均为，则（ ）
A．B．AB与平面所成的角为
C．D．与平面所成的角为
二、多选题
7．（2023·全国·高考真题）已知圆锥的顶点为P，底面圆心为O，AB为底面直径，，，点C在底面圆周上，且二面角为45°，则（ ）．
A．该圆锥的体积为B．该圆锥的侧面积为
C．D．的面积为
8．（2022·全国·高考真题）已知正方体，则（ ）
A．直线与所成的角为B．直线与所成的角为
C．直线与平面所成的角为D．直线与平面ABCD所成的角为
参考答案：
1．B
【分析】解法一：根据台体的体积公式可得三棱台的高，做辅助线，结合正三棱台的结构特征求得，进而根据线面夹角的定义分析求解；解法二：将正三棱台补成正三棱锥，与平面ABC所成角即为与平面ABC所成角，根据比例关系可得，进而可求正三棱锥的高，即可得结果.
【详解】解法一：分别取的中点，则，
可知，
设正三棱台的为，
则，解得，
如图，分别过作底面垂线，垂足为，设，
则，，
可得，
结合等腰梯形可得,
即，解得，
所以与平面ABC所成角的正切值为；
解法二：将正三棱台补成正三棱锥，
则与平面ABC所成角即为与平面ABC所成角，
因为，则，
可知，则，
设正三棱锥的高为，则，解得，
取底面ABC的中心为，则底面ABC，且，
所以与平面ABC所成角的正切值.
故选：B.
2．A
【分析】根据线面平行的判定定理即可判断①；举反例即可判断②④；根据线面平行的性质即可判断③.
【详解】对①，当，因为，，则，
当，因为，，则，
当既不在也不在内，因为，，则且，故①正确；
对②，若，则与不一定垂直，故②错误；
对③，过直线分别作两平面与分别相交于直线和直线，
因为，过直线的平面与平面的交线为直线，则根据线面平行的性质定理知，
同理可得，则，因为平面，平面，则平面，
因为平面，，则，又因为，则，故③正确；
对④，若与和所成的角相等，如果，则，故④错误；
综上只有①③正确，
故选：A.
3．C
【分析】根据给定条件，推导确定线面角，再利用余弦定理、正弦定理求解作答.
【详解】取的中点，连接，因为是等腰直角三角形，且为斜边，则有，
又是等边三角形，则，从而为二面角的平面角，即，

显然平面，于是平面，又平面，
因此平面平面，显然平面平面，
直线平面，则直线在平面内的射影为直线，
从而为直线与平面所成的角，令，则，在中，由余弦定理得：
，
由正弦定理得，即，
显然是锐角，，
所以直线与平面所成的角的正切为.
故选：C
4．A
【分析】证明平面，分割三棱锥为共底面两个小三棱锥，其高之和为AB得解.
【详解】取中点，连接，如图，
是边长为2的等边三角形，，
，又平面，，
平面，
又，，
故，即，
所以，
故选：A
5．A
【分析】证明平面，即可判断A；如图，以点为原点，建立空间直角坐标系，设，分别求出平面，，的法向量，根据法向量的位置关系，即可判断BCD.
【详解】解：在正方体中，
且平面，
又平面，所以，
因为分别为的中点，
所以，所以，
又，
所以平面，
又平面，
所以平面平面，故A正确；
选项BCD解法一：
如图，以点为原点，建立空间直角坐标系，设，
则，
，
则，，
设平面的法向量为，
则有，可取，
同理可得平面的法向量为，
平面的法向量为，
平面的法向量为，
则，
所以平面与平面不垂直，故B错误；
因为与不平行，
所以平面与平面不平行，故C错误；
因为与不平行，
所以平面与平面不平行，故D错误，
故选：A.
选项BCD解法二：
解：对于选项B，如图所示，设，，则为平面与平面的交线，
在内，作于点，在内，作，交于点，连结，
则或其补角为平面与平面所成二面角的平面角，
由勾股定理可知：，，
底面正方形中，为中点，则，
由勾股定理可得，
从而有：，
据此可得，即，
据此可得平面平面不成立，选项B错误；
对于选项C，取的中点，则，
由于与平面相交，故平面平面不成立，选项C错误；
对于选项D，取的中点，很明显四边形为平行四边形，则，
由于与平面相交，故平面平面不成立，选项D错误；
故选：A.
6．D
【分析】根据线面角的定义以及长方体的结构特征即可求出．
【详解】如图所示：
不妨设，依题以及长方体的结构特征可知，与平面所成角为，与平面所成角为，所以，即，，解得．
对于A，，，，A错误；
对于B，过作于，易知平面，所以与平面所成角为，因为，所以，B错误；
对于C，，，，C错误；
对于D，与平面所成角为，，而，所以．D正确．
故选：D．
7．AC
【分析】根据圆锥的体积、侧面积判断A、B选项的正确性，利用二面角的知识判断C、D选项的正确性.
【详解】依题意，，，所以，
A选项，圆锥的体积为，A选项正确；
B选项，圆锥的侧面积为，B选项错误；
C选项，设是的中点，连接，
则，所以是二面角的平面角，
则，所以，
故，则，C选项正确；
D选项，，所以，D选项错误.
故选：AC.

8．ABD
【分析】数形结合，依次对所给选项进行判断即可.
【详解】如图，连接、，因为，所以直线与所成的角即为直线与所成的角，
因为四边形为正方形，则，故直线与所成的角为，A正确；
连接，因为平面，平面，则，
因为，，所以平面，
又平面，所以，故B正确；
连接，设，连接，
因为平面，平面，则，
因为，，所以平面，
所以为直线与平面所成的角，
设正方体棱长为，则，，，
所以，直线与平面所成的角为，故C错误；
因为平面，所以为直线与平面所成的角，易得，故D正确.
故选：ABD
【模拟精练】
一、单选题
1．（2024·湖南·二模）如图，在三棱柱中，分别为的中点，则下列说法错误的是（ ）
A．四点共面B．
C．三线共点D．
2．（23-24高一下·湖南常德·期中）设，是两条不同的直线，是两个不同的平面，则下列结论正确的是（ ）
A．若，则B．若，则
C．若，则是异面直线D．若，则或，是异面直线
3．（21-22高二上·贵州遵义·期末）如图，在四棱锥中，平面，四边形为平行四边形，且为的中点，则异面直线与所成的角的余弦值为（ ）
A．B．C．D．
4．（23-24高二上·北京·阶段练习）设a，b是两条不同的直线，，是两个不同的平面，则下列命题正确的是（ ）
A．若，，，则B．若，，则
C．若，，，则D．若，，，则
5．（2024·广东深圳·二模）已知正方体，过点A且以为法向量的平面为，则截该正方体所得截面的形状为（ ）
A．三角形B．四边形C．五边形D．六边形
6．（23-24高三上·陕西商洛·阶段练习）如图所示，在棱长为2的正方体中，点在棱上，且，则点到平面的距离之和为（ ）

A．B．C．D．
7．（23-24高三上·山东济宁·阶段练习）如图1，某广场上放置了一些石凳供大家休息，这些石凳是由正方体截去八个一样的正三棱锥得到的，它的所有棱长均相同，数学上我们称之为半正多面体（semiregular slid），亦称为阿基米德多面体，如图2，设，则平面与平面之间的距离是（ ）
A．B．C．D．
8．（2023·四川泸州·二模）《九章算术》中关于“刍童”（上、下底面均为矩形的棱台）体积计算的注释：将上底面的长乘以二与下底面的长相加，再与上底面的宽相乘，将下底面的长乘以二与上底面的长相加，再与下底面的宽相乘，把这两个数值相加，与高相乘，再取其六分之一．现有“刍童”，其上、下底面均为正方形，若，且每条侧棱与底面所成角的正切值均为，则该“刍童”的体积为（ ）
A．224B．448C．D．147
二、多选题
9．（2024·辽宁·二模）已知是两条不同的直线，是两个不同的平面，则下列命题为真命题的有（ ）
A．若，则
B．若，则
C．若，则
D．若为异面直线，，则
10．（2024·湖南娄底·一模）已知是空间中三条不同的直线，是空间中两个不同的平面，下列命题不正确的是（ ）
A．若，则
B．若，则
C．若，则或.
D．若，则，
11．（2024·辽宁沈阳·二模）已知正四棱锥的所有棱长均相等，为顶点在底面内的射影，则下列说法正确的有（ ）
A．平面平面
B．侧面内存在无穷多个点，使得平面
C．在正方形的边上存在点，使得直线与底面所成角大小为
D．动点分别在棱和上（不含端点），则二面角的范围是
12．（2024·安徽芜湖·二模）如图，多面体由正四棱锥和正四面体组合而成，其中，则下列关于该几何体叙述正确的是（ ）
A．该几何体的体积为B．该几何体为七面体
C．二面角的余弦值为D．该几何体为三棱柱
13．（2024·黑龙江齐齐哈尔·一模）已知四面体的各个面均为全等的等腰三角形，且.设为空间内任一点，且五点在同一个球面上，则（ ）
A．
B．四面体的体积为
C．当时，点的轨迹长度为
D．当三棱锥的体积为时，点的轨迹长度为
14．（2024·江西上饶·二模）在四棱锥中，是正方形，，，，为棱上一点，则下列结论正确的是（ ）
A．点到平面的距离为1
B．若，则过点，，的平面截此四棱锥所得截面的面积为
C．四棱锥外接球的表面积为
D．直线与平面所成角的正弦值的最大值为
三、填空题
15．（23-24高三下·广东深圳·期中）在长方体中，，点为侧面内一动点，且满足平面，则的最小值为 ，此时点到直线的距离为 .
16．（2024·广东·二模）将一个直角三角板放置在桌面上方，如图，记直角三角板为，其中，记桌面为平面.若，且与平面所成的角为，则点到平面的距离的最大值为 .
四、解答题
17．（2024·四川泸州·三模）如图，在四棱锥中，底面是矩形，，，与交于点，底面，，点，分别是棱，的中点，连接，，.

(1)求证：平面平面；
(2)求三棱锥的体积.
18．（2024·上海松江·二模）如图，在四棱锥中，底面为菱形，平面，为的中点.
(1)设平面与直线相交于点，求证：；
(2)若，，，求直线与平面所成角的大小.
参考答案：
1．D
【分析】对于AB，利用线线平行的传递性与平面公理的推论即可判断；对于C，利用平面公理判断得，的交点在，从而可判断；对于D，举反例即可判断.
【详解】对于AB，如图，连接，，
因为是的中位线，所以，
因为，且，所以四边形是平行四边形，
所以，所以，所以四点共面，故AB正确；
对于C，如图，延长，相交于点，
因为，平面，所以平面，
因为，平面，所以平面，
因为平面平面，
所以，所以三线共点，故C正确；
对于D，因为，当时，，
又，则，故D错误.
故选：D.
2．D
【分析】利用空间中线、面的位置关系一一判定选项即可.
【详解】
对于A，可设为平面，显然，但，故A错误；
对于B，可设为平面，显然，但，故B错误；
对于C，可设分别为平面，平面，
显然，但，故C错误；
对于D，若，则两平面不会有交点，所以或，是异面直线，
故D正确.
故选：D
3．B
【分析】分别取的中点，连接，则可证明为异面直线SC与DE所成的角，分别在三角形中由勾股定理求出，和的长度，利用余弦定理计算得到答案.
【详解】如图所示：
分别取的中点，连接.
由且可得是等边三角形，
则且，且，故且，
所以四边形为平行四边形，故，
因为，所以为异面直线SC与DE所成的角（或其补角），
因为平面，平面，∴，，
故和均为直角三角形，
所以，，
，
由余弦定理得.
则异面直线与所成的角的余弦值为.
故选：B
4．D
【分析】对于ABC：借助于长方体分析判断；对于D：根据面面平行的性质以及线面垂直的性质分析判断.
【详解】在长方体，令平面是平面，
对于A，若平面为平面，直线为直线，直线为直线，
显然，，，此时直线是异面直线，不平行，故A错误；
对于B，若平面为平面，
则，直线为直线，直线为直线，
显然，但，此时直线不与平面平行，故B错误；
对于C，若平面为平面，直线为直线，直线为直线，
显然，，，此时直线平行，不垂直，故C错误；
对于D，过直线作平面与平面相交，设交线为，
因为，，，且，可得，
又因为，，则，所以，故D正确．
故选：D．
5．A
【分析】作出辅助线，根据线面垂直的判定定理得到⊥平面，故平面即为平面，得到截面的形状.
【详解】连接，
因为平面，平面，
所以，
又四边形为正方形，所以，
又，平面，
所以平面，
因为平面，
所以，
同理可证明，
因为，平面，
故平面，
故平面即为平面，
则截该正方体所得截面的形状为三角形.
故选：A
6．B
【分析】根据条件确定点P的位置，利用线面平行把点到平面的距离分别转化点到平面的距离求解即可.
【详解】在棱长为2的正方体中，平面，平面，
则，由，得，
在中，，则，即点为中点，
又平面，平面，因此平面，
于是点到平面的距离等于点到平面的距离，同理点到平面的距离
等于点到平面的距离，连接，过分作的垂线，垂足分别为，如图，

由，得，解得，
在中，，则，
所以点到平面的距离之和为.
故选：B
7．D
【分析】不妨记正方体为，设对角线分别交平面和平面于点，，可推出即为平面与平面的距离，结合等体积法求得，结合对称性求得即可．
【详解】如图，不妨记正方体为，，，
故四边形是平行四边形，所以，
又，分别为，的中点，
所以，同理，
所以，又平面，平面，
所以平面，同理平面，
又，，平面，
所以平面平面，
设对角线分别交平面和平面于点，，
因为平面，平面，
所以，
连接，因为分别为的中点，
故，又，平面，，
所以平面，又平面，
所以，同理，
又，，平面，
所以平面，
又平面平面，
所以平面，
即为平面与平面的距离，
则，
由正方体棱长为得，
由题意得，为等边三角形，
故，
根据，
得，
解得，
根据对称性知，
所以，
则平面与平面的距离为．
故选：D
【点睛】方法点睛：求点到平面的距离方法，一是建立空间直角坐标系，利用空间向量求解；二是利用等体积法求解；三是作出辅助线，在三角形中结合余弦定理等方法进行求解.
8．B
【分析】根据题意结合图形得到是“刍童”其中一条侧棱与与底面所成角的平面角，从而求得该刍童的高，进而根据刍童的体积公式即可求得结果．
【详解】连接，交于点，连接，交于点，连接，过作，如图，
.
因为“刍童”上、下底面均为正方形，且每条侧棱与底面所成角的正切值均相等，
所以底面，又，所以底面，
所以是“刍童”其中一条侧棱与底面所成角的平面角，则，
因为，所以，
易知四边形是等腰梯形，则，
所以在中，，则，即“刍童”的高为，
则该刍童的体积.
故选：B．
9．AD
【分析】根据直线与平面的位置关系，由线面垂直、线面平行的性质逐项判断即可得出结论.
【详解】对于A，若，是两个不同的平面，则可得，即A正确；
对于B，若，当都平行于两平面的交线时，，可知B错误；
对于C，若，则可能会，即C错误；
对于D，若，又为异面直线，所以，即D正确.
故选：AD
10．ABC
【分析】由题意分别进行判断，错误的选项指明错误点.
【详解】对，需要补上不平行才成立，否则可能与相交或平行，故错误；
对，若，则或，故错误；
对，有可能且且，故错误；
对D，若，则，故D正确.
故选：ABC.
11．BD
【分析】过作直线，则为平面与平面的交线，取中点中点F，连接，求得可判断A；取中点中点H，连接，可得，，可判断B；由已知可知当Q在正方形各边中点时，与底面所成的角最大，可得，判断C；作垂直于，连接，则为二面角的平面角，求得二面角范围是，判断D.
【详解】已知所有棱长都相等，不妨设为1．
对于A：过S作直线，因为，所以，
所以为平面与平面的交线，
取中点中点F，连接，由正四棱锥，
可得，所以，
所以为二面角的平面角，连接，
在中，
所以平面与平面不垂直，故A错误；
对于B：取中点中点H，连接，
因为，又平面 ，平面，
所以平面，平面，又，
所以平面平面，所以当时，平面，这样的点P有无穷多，故B正确；
对于C：由已知可知当Q在正方形各边中点时，与底面所成的角最大，，所以，所以不布存Q使得与底面成的角为，故C错误；
对于D：作垂直于，连接，
因为平面，又平面，所以，
又，所以平面，因为平面，所以，
因为则为二面角的平面角，
当都无限向点B靠拢时，；当时，，
所以二面角范围是，故D正确．
故选：BD.
12．ACD
【分析】选项A可以分别求正四棱锥和正四面体的体积即可；
选项C先确定二面角的平面角为，在三角形中利用余弦定理可得；
选项D先根据二面角与二面角的关系确定四点共面，再证得平面平面，三个侧面都是平行四边形即可；
选项B根据选项D三棱柱有5个面，可判断错误.
【详解】
如图：在正四面体中中，为的中点，连接，连接作于，
则为的中心，为正四面体中的高，
因， ，，，
，
在正四面体中中，为的中点，所以，，
故为二面角的一个平面角，
如图：在正四棱锥中，由题意，
连接，交于点，连接，则为正四棱锥的高，
，，
，
该几何体的体积为，故A正确，
取的中点，连接，，
由题意正四棱锥的棱长都为1，所以，，
故即为二面角的一个平面角，
其中，，
在中，，故C正确，
因，可知二面角与二面角所成角互补，
故平面与为同一平面，同理，平面和平面也为同一平面，
故该几何体有5个面，B错误，
因四点共面，且和都为等边三角形，易知，且，故侧面为平行四边形，
又平面,平面，所以平面，
同理平面，且侧面为平行四边形，
又，平面，平面，
所以平面平面，又侧面为正方形，
故多面体即为三棱柱，故D正确，
故选：ACD
13．AC
【分析】根据线面的垂直可判断线线垂直，判断A；根据棱锥的体积公式可判断B；根据条件，确定轨迹的形状，结合圆的周长求得轨迹长度或范围，即可判断C，D.
【详解】对于A，依题意，可知，
设F为的中点，连接，则，
而平面，故平面，
平面，故，A正确；
对于B，将四面体放入长方体中，设长方体的相邻三条棱长分别为，
则，解得，
由于，即异面直线和的距离为，且平面，，
所以四面体的体积为，B错误；
对于C，由以上分析可知，四面体的外接球半径为，
由，知点的轨迹为一个圆，设轨迹圆的半径为，
则，解得，
所以的轨迹长度为，C正确；
对于D，由题意可得,
故的外接圆半径为，
所以球心到所在平面的距离为，
设三棱锥的高为h，
由三棱锥的体积为时，可得，
故，
又由，故E点轨迹为外接球上平行于平面且到平面的距离为的两个截面圆，
其中一个圆为外接球的大圆，
所以点的轨迹长度大于，D错误，
故选：AC.
【点睛】难点点睛：本题考查了四面体中的线面以及线线的位置关系，以及体积和空间几何体中的轨迹问题，难点在于要发挥空间想象，明确空间几何体中的线线位置关系，特别是选项D中要明确E点轨迹，从而确定轨迹长度或其范围.
14．ABD
【分析】设点到平面的距离为，结合，求得，可判定A正确；取中点为，连接，，可得截面为直角梯形，进而可判定B正确；结合球的截面的性质，可求得四棱锥外接球的半径为，结合球的表面积公式，可判定C不正确；作和 ，证得平面平面，将与平面所成的角转化为，设，求得，结合二次函数的性质，可判定D正确.
【详解】对于A选项，因为，，又，且，面，
所以面，又因为，所以平面，
因为，且，
可得到平面的距离为，即三棱锥的高为，
设点到平面的距离为，且，
由，可得，得.
所以点到平面的距离为1，所以A正确；
对于B选项，因为，所以点为棱的中点，
取中点为，连接，，则平面即为平面截此四棱锥所得的截面.
且点是的中点，点为棱的中点，
所以在中，是的中位线，则，且，
又因为四边形是正方形，则，所以，
因为面，且面，面，所以.
所以四边形是以为下底、为上底，为高的直角梯形，
因为，在等腰中，，且平分，
可得，
则平面截此四棱锥所得截面的面积为，所以B正确；
对于C选项，又因为，，且，
所以，即，其中为外接圆半径，
因为正方形的中心到面的距离等于其边长的一半，即，故四棱锥外接球的半径为.
所以四棱锥外接球的表面积为，所以C不正确；
对于D选项，过点作，再过点作，使得分别在线段上，连接.
根据线面平行的判定定理，可得平面，平面，
因为，且平面，所以平面平面，
又因为平面，所以平面，即平面.
所以即为与平面所成的角，即为与平面所成的角.
由于平面，在平面内，故.
从而在直角中，可得.
设，由，可得，
所以，所以.
由于，故在中，由余弦定理可得，
在中，由余弦定理可得，
在直角中，可得，且当时，不等号取等.
所以的最大值是，所以D正确.
故选：ABD.
【点睛】解题方法点拨：
1、立体几何中的动态问题主要包括：空间动点轨迹的判断，求解轨迹的长度及动角的范围等问题；
2、解答方法：一般时根据线面平行，线面垂直的判定定理和性质定理，结合圆或圆锥曲线的定义推断出动点的轨迹，有时也可以利用空间向量的坐标运算求出动点的轨迹方程；
3、对于线面位置关系的存在性问题，首先假设存在，然后再该假设条件下，利用线面位置关系的相关定理、性质进行推理论证，寻找假设满足的条件，若满足则肯定假设，若得出矛盾的结论，则否定假设；
4、对于探索性问题用向量法比较容易入手，一般先假设存在，设出空间点的坐标，转化为代数方程是否有解的问题，若由解且满足题意则存在，若有解但不满足题意或无解则不存在.
15． /
【分析】由题意，根据线面平行的判定定理和面面平行的判定定理可证得平面平面，由面面平行的性质确定点的轨迹为线段，且当取最小值时，建立如图空间直角坐标系，利用空间向量法求解点线距离即可.
【详解】如图所示，因为且，故四边形为平行四边形，则，
因为平面平面，所以平面，
同理可证平面，因为平面，
所以平面平面，因为平面，要使得平面，
则平面，因为平面平面，
故点的轨迹为线段，当取最小值时，，则为的中点，
则.
以为原点，的方向分别为，轴建立空间直角坐标系，
易知，
取，
则，
所以点到直线的距离为.
故答案为：；
【点睛】关键点点睛：解决本题的关键是通过平面平面确定点的轨迹为线段，即当时取最小值，注重考查学生的数学运算和逻辑推理能力.
16．
【分析】作出辅助线，判断出当四点共面时，点A到的距离最大，进而算出，最后得到答案．
【详解】如图，过作⊥，交于，过A作⊥，交于，
因为在中，,，
则，当四点共面时，点A到的距离最大．
因为⊥，所以是BC与平面所成的角，则，则，
于是，，即A到的最大距离为．
故答案为：．
17．(1)见解析
(2)
【分析】（1）根据中位线定理和面面平行的判定定理即可证明；
（2）根据等体积法即可求解.
【详解】（1）因为底面是矩形，AC与BD交于点O
所以O为AC中点，
点E是棱PA的中点，F分别是棱PB的中点，
所以OE为三角形的中位线，OF为三角形的中位线，
所以,，
平面，平面，平面，
平面，平面，平面，
而,平面，平面，
平面平面.
（2）因为底面ABCD是矩形，，，
所以为等边三角形，所以，
所以，
根据体积相等法可知，
，
故三棱锥的体积为.
18．(1)证明见解析
(2)
【分析】（1）根据线面平行的判定定理，证出平面，然后根据平面平面，利用线面平行的性质定理证出；
（2）连接，取中点，连接、，根据线面垂直的判定定理，证出平面，可得是直线与平面的所成角，然后在中利用锐角三角函数的定义算出答案．
【详解】（1）证明：平面与直线相交于点，平面平面，
四边形是菱形，，
平面，平面，平面，
平面，平面平面，
；
（2）连接，取中点，连接、，
菱形中，，，是等边三角形，
是中点，，
平面，平面，，
、平面，，平面．
是直线与平面的所成角，
是中点，，．
平面，平面，，
为中点，，中，，
等边中，高，
中，，
可得，即直线与平面的所成角等于．
题号
1
2
3
4
5
6
7
8


答案
B
A
C
A
A
D
AC
ABD


题号
1
2
3
4
5
6
7
8
9
10
答案
D
D
B
D
A
B
D
B
AD
ABC
题号
11
12
13
14






答案
BD
ACD
AC
ABD