广东省东莞市2024-2025学年八年级上学期12月月考数学试卷(含答案)

这是一份广东省东莞市2024-2025学年八年级上学期12月月考数学试卷(含答案)，共17页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．下面四个汉字中,可以看做是轴对称图形的是( )
A.B.C.D.
2．在下列各原命题中,逆命题是假命题的是( )
A.两直线平行,同旁内角互补
B.如果两个三角形全等,那么这两个三角形的对应边相等
C.如果两个三角形全等,那么这两个三角形的对应角相等
D.两个相等的角是对顶角
3．若等腰三角形的两条边长分别为6cm和13cm,则它的周长为( )
A.26B.32C.26或32D.19或26
4．如图,,,要得到,可以添加( )
A.B.C.D.
5．下列各式计算正确的是( )
A.B.
C.D.
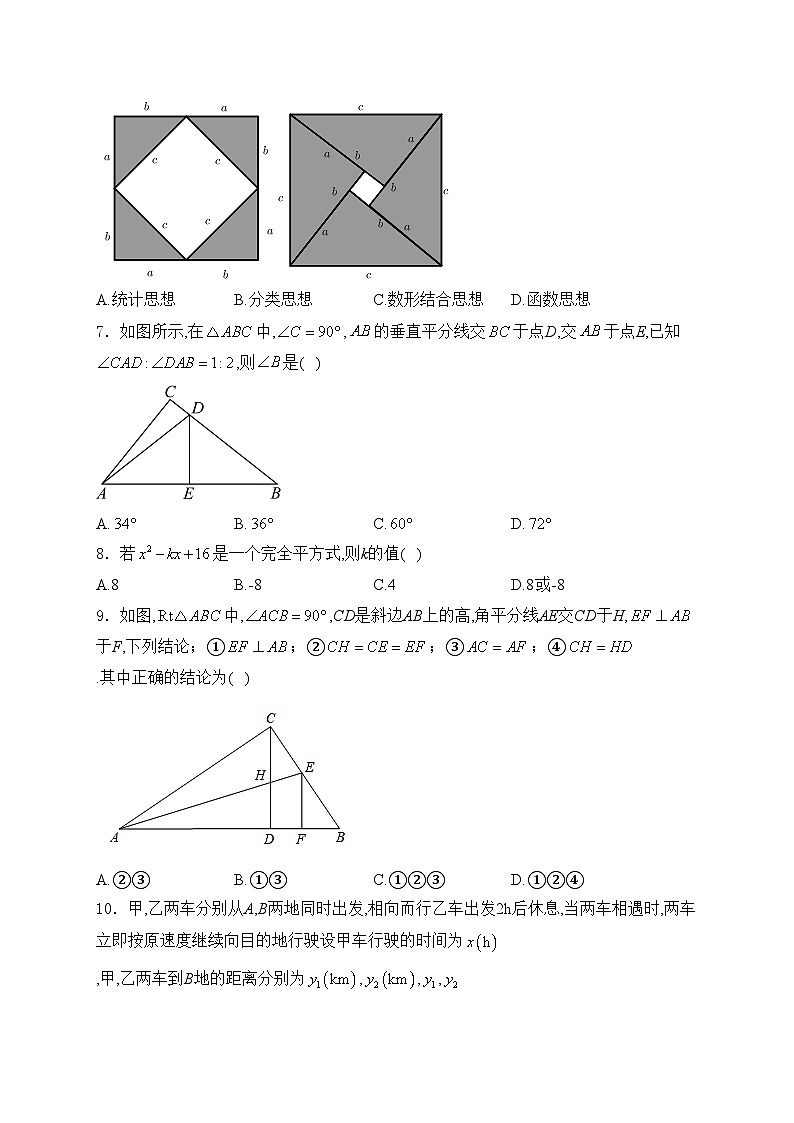
6．在勾股定理的学习过程中,我们已经学会了运用以下图形,验证著名的勾股定理：这种根据图形直观推论或验证数学规律和公式的方法,简称为“无字证明”.实际上它也可用于验证数与代数,图形与几何等领域中的许多数学公式和规律,它体现的数学思想是( )
A.统计思想B.分类思想C.数形结合思想D.函数思想
7．如图所示,在中,,的垂直平分线交于点D,交于点E,已知,则是( )
A.B.C.D.
8．若是一个完全平方式,则k的值( )
A.8B.-8C.4D.8或-8
9．如图,中,,CD是斜边AB上的高,角平分线AE交CD于H,于F,下列结论；①；②；③；④.其中正确的结论为( )
A.②③B.①③C.①②③D.①②④
10．甲,乙两车分别从A,B两地同时出发,相向而行乙车出发2h后休息,当两车相遇时,两车立即按原速度继续向目的地行驶设甲车行驶的时间为,甲,乙两车到B地的距离分别为,,,关于x的函数图象如图下列结论：①甲车的速度是；②乙车休息了0.5h；③两车相距akm时,甲车行驶了正确的是( )
A.①②B.①③C.②③D.①②③
二、填空题
11．已知,则______.
12．正多边形的每个内角等于,则这个正多边形的边数为____________条.
13．______.
14．若点和点关于y轴对称,则点______.
15．等腰三角形中一个角为,则这个等腰三角形的顶角的度数为______.
16．如图所示,在矩形中,厘米,厘米,点P沿边从点A开始向点B以1厘米/秒的速度移动,点Q沿从点B开始向点C以2厘米/秒的速度移动,P、Q同时出发,用t(秒)表示移动的时间.如果当移动的时间在,那么四边形的面积与矩形的面积关系的规律是______.
17．我国宋代数学家杨辉发现了展开式系数的规律：
以上系数三角表称为“杨辉三角”,根据上述规律,展开式的系数和是______.
三、解答题
18．化简.
19．如图,已知,,,求证：.
20．如图所示,是的角平分线,于点E.的面积为,,,则的长为多少?
21．如图,三个顶点的坐标分别为、、.
(1)画出关于y轴的对称图形,并写出点的坐标；
(2)在y轴上求作一点P,使的周长最小,并求出点P的坐标及的周长最小值.
22．先化简,再求值：,其中,.
23．已知实数a、b、c满足.
(1)求a、b、c的值；
(2)判断以a、b、c为边能否构成三角形？若能构成三角形,判别此三角形的形状,并求出三角
形的面积；若不能,请说明理由.
24．如图,在四边形ABCD中,,E为CD的中点,连接AE、BE,,延长AE交BC的延长线于点F.求证：
(1)；
(2).
25．我们现给出如下结论：“直角三角形斜边上的中线等于斜边的一半”,图形语言说明：如图1所示,在中,,由是中线,可得.
请结合上述结论解决如下问题：
已知：P是边上的一动点(不与A,B集合),分别过点A、点B向直线作垂线,垂是分别为点E点F,Q为边的中点.
(1)如图2所示,当点P与点Q重合时,与的位置关系是____________,与的数量关系是____________.
(2)如图3所示,当点P在线段上不与点Q重合时,试判断与的数量关系,并给与证明.
(3)如图4所示,当点P在线段的延长线上时,此时(2)中的结论是否成立？若成立,请写出证明过程；若不成立,请说明理由.
参考答案
1．答案：A
解析：根据轴对称图形的定义可知,只有选项A的图形可以沿一条直线折叠使得直线两旁的部分能够互相重合,故A选项是轴对称图形.
故选：A.
2．答案：C
解析：A逆命题是同旁内角互补,两直线平行,是真命题,
∴A不符合题意；
B逆命题是如果两个三角形的对应边相等,那么这两个三角形全等,是真命题,
∴B不符合题意；
C逆命题是如果两个三角形的对应角相等,那么这两个三角形全等,是假命题,
∴C符合题意；
D逆命题是如果两个角是对顶角,那么这两个角相等,是真命题,
∴D不符合题意；
故选C.
3．答案：B
解析：当13cm为底边长时,则两条腰长为6cm,但,不构成三角形,舍去；
当6cm为底边长时,则两条腰长为13cm,满足,构成三角形,
∴该等腰三角形的周长为,
故选：B.
4．答案：B
解析：A、∵,
∴,
又∵,只有两组相等的条件,
∴不能判定,不符合题意；
B、∵,
∴,
又∵,,
∴,
∴可以证明,符合题意；
C、∵,
又∵,,
两边及其一边的对角对应相等不能证明两个三角形全等,
∴不能证明,不符合题意；
D、∵,
又∵,,
两边及其一边的对角对应相等不能证明两个三角形全等,
∴不能证明,不符合题意.
故选：B.
5．答案：D
解析：A、,故本选项错误；
B、,故本选项错误；
C、,故本选项错误；
D、,故本选项正确.
故选：D.
6．答案：C
解析：根据图形直观推论或验证数学规律和公式的方法,
如勾股定理的推导是根据图形面积转换得以证明的,
由图形到数学规律的转化体现的数学的思想为：数形结合思想,
故选：C.
7．答案：B
解析：∵的垂直平分线交于点D,
∴,
∴是等腰三角形,,
∵,
∴设,则,
∴,
∴,
即,
故选：B.
8．答案：D
解析：∵是一个完全平方式,
∴,
解得：,
故选：D.
9．答案：C
解析：∵,
∴,
∵CD是AB边上的高,
∴,
∴,
∴,故①说法正确；
∵AE是的角平分线,,,
∴,,,
∵,,
∴,
∴,故②说法正确；
∵,,,
∴,
∴,故③说法正确；
假设,
又∵,,
∴,
∴,
∵,
∴,
又∵D与F不重合,
∴,
∴,故④说法错误,
故选C.
10．答案：A
解析：由函数图象可知,甲5小时到达,速度为,故①正确；
甲与乙相遇时,时间为,所以乙休息了,②正确；
乙的速度为：,
在2小时时,甲乙相距,
∴在2小时前,若两车相距时,,解得,
当两车相遇后,即2.5小时后,若两车相距akm时,,
解得,
∴两车相距时,甲车行驶了或,故③错误；
故选：A.
11．答案：
解析：由题意得,,,
解得：,,
所以,
故答案为：.
12．答案：12
解析：多边形内角和为,则每个内角为／,,所以应填12.
13．答案：
解析：
故答案为：.
14．答案：0
解析：点和点关于y轴对称,
,,
解得：,,
,
故答案为：0.
15．答案：
解析：,
的角只能为等腰三角形的顶角,
这个等腰三角形的顶角的度数为,
故答案为：.
16．答案：当时,四边形的面积总是矩形的面积一半
解析：由题意可知,,,,
,,,,
,,
,
,
当时,四边形的面积总是矩形的面积一半,
故答案为：当时,四边形的面积总是矩形的面积一半.
17．答案：
解析：解展开式中所有项的系数和为,
展开式中所有项的系数和为,
展开式中所有项的系数和为,
,
展开式的系数和是,
故答案为：.
18．答案：
解析：
.
19．答案：见解析
解析：证明：∵,
∴.
即,
在和中,
∴.
∴.
20．答案：2
解析：如图,作于F,
是的角平分线,,,
,
的面积为,,,
,即,
.
21．答案：(1)
(2)
解析：(1)如图所示,由图可知；
(2)如图所示,点P即为所求点.
设直线的解析式为,
∵,,
∴,解得,
∴直线的解析式为,
∴点P坐标,
∴的周长最小值.
22．答案：；2022
解析：原式
.
当,时,
原式.
23．答案：(1),,
(2)直角三角形；面积为
解析：(1)∵实数a,b,c满足
∴,,,
∴,,；
(2)∵,,,
∴,,,
∴,
∴以a,b,c为边的三角形是直角三角形,
∴该三角形的面积为：.
24．答案：(1)证明见解析
(2)证明见解析
解析：(1),
,,
点E是CD的中点,
,
在和中,,
,
；
(2)由(1)已证：,
,
又,
是线段AF的垂直平分线,
,
由(1)可知,,
.
25．答案：(1)；
(2),证明见解析
(3)成立,证明见解析
解析：(1)如图1,
当点P与点Q重合时,与的位置关系是,与的数量关系是,
理由：
为的中点,
,
,,
,,
在和中
,
,
,
故答案为：；；
(2)
证明：延长交于D,
,,
,
(3)当点P在线段延长线上时,此时(2)中结论成立
证明：延长交的延长于D
∵,
∴
.