初中数学湘教版（2024）七年级下册（2024）1.2 乘法公式完整版ppt课件

这是一份初中数学湘教版（2024）七年级下册（2024）1.2 乘法公式完整版ppt课件，文件包含新湘教版初中数学七年级下册123《运用乘法公式进行计算和推理》课件pptx、新湘教版初中数学七年级下册123《运用乘法公式进行计算和推理》教案docx等2份课件配套教学资源，其中PPT共18页， 欢迎下载使用。
1.熟练地运用乘法公式进行计算.
正确选择乘法公式进行运算.
综合运用平方差和完全平方公式进行多项式的计算.
2.能正确地根据题目的要求选择不同的乘法公式进行运算.
3.提高学生对乘法公式综合运用的能力，分析、解决问题的能力.
4.培养学生实事求是、科学严谨的学习态度.
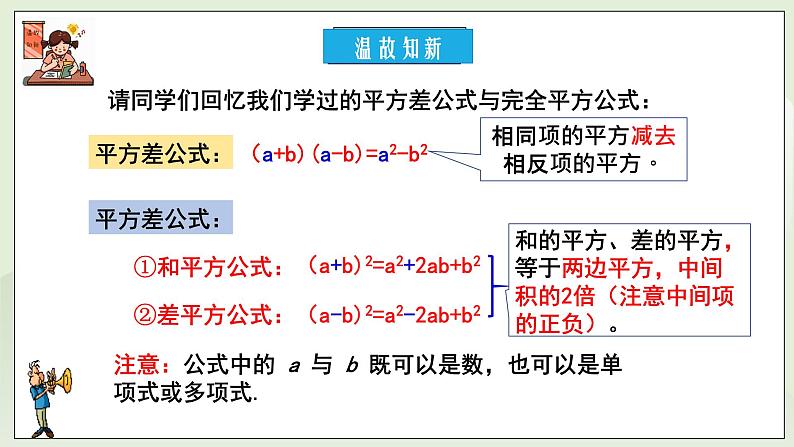
请同学们回忆我们学过的平方差公式与完全平方公式：
注意：公式中的 a 与 b 既可以是数，也可以是单项式或多项式.
（a+b)(a-b)=a2-b2
（a+b)2=a2+2ab+b2
（a-b)2=a2-2ab+b2
相同项的平方减去相反项的平方。
和的平方、差的平方，等于两边平方，中间积的2倍（注意中间项的正负）。
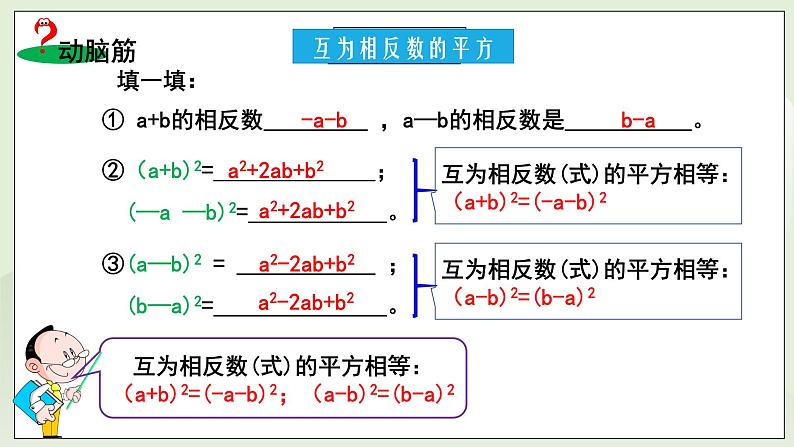
① a+b的相反数 ，a—b的相反数是 。
②（a+b)2= ； (—a —b)2= 。
③(a—b)2 = ； (b—a)2= 。
互为相反数(式)的平方相等：（a+b)2=(-a-b)2
互为相反数(式)的平方相等：（a-b)2=(b-a)2
运用完全平方公式计算：
(1)(-x+1)2
解：原式=(x-1)2
=x2-2∙x∙1+12
底数的第一项是负号，可将整个底数变成相反数。
解：原式=(2x+3)2
=(2x)2+2∙2x∙3+32
(2)(-2x-3)2
运用乘法公式计算：(x + 1)(x2+ 1)(x - 1).
解：原式= (x+1)(x-1)(x2+1) = (x2-1)(x2+1) = x4-1
例7 运用乘法公式计算：（1）(a+ b + c)2； （2）（a- b + c)(a+ b - c).
是一个三项式，如果将（a+b)看成一个整体，就满足了完全平方公式。
解：原式=[(a+b)+c]2
=(a+b)2+2﹒(a+b)﹒c+c2
=a2+2ab+b2 +2ac+2bc+c2
解：原式=[a-(b-c)][a+(b-c)]
=a2-(b2-2bc+c2)
=a2-b2+2bc-c2
例8 运用乘法公式计算：（1）(a+ b)2 +(a- b)2；
解：原式=a2+2ab+b2
（2）(a+ b)2 -(a- b)2
+a2 -2ab+b2
将(a+ b)2和(a- b)2都看成一个整体，就可以使用平方差公式
解：原式=[(a+ b)+(a- b)][(a+ b)-(a- b)]
例9 运用乘法公式计算：(x + y)3.
解：原式=(x+y)2(x+y)
=(x2 + 2xy + y2)(x + y)
=x3+2x2y+xy2+yx2+2xy2+y3
=x3+3x2y+3xy2+y3
（1） 152 = =100×1× +25；
（3） 352 = =100×3× +25
（2） 252 = =100×2× +25
由此猜测：十位数字是a，个位数字是5的两位数可以表示为 ，它的平方可表示为100× × + 。
等于其十位数字a与a+1的积的100倍，再加上25。
证明：十位数字是a，个位数字是5的两位数是10a+5.
(10a)2 + 2﹒10a﹒5+52
= 100a2+100a+25.
又∵100a(a+1)+25 =100a2 +100a+25，
∴（10a+5)2 =100a(a+1)+25.
练 习
1. 运用乘法公式计算：
（1）(x-2)(x+2)(x2+4）； （2）(x+1)2(x-1)2；
（3）(a-b-c)2； （4）(x+2y-1)(x+2y+1）；
（5）(2x+y-1)(2x-y+1）.
解：原式=(x2-4)(x2+4）
解：原式=[(x+1)(x-1)]2
解：原式=[a-(b+c)]2
=a2-2a(b+c)+(b+c)2
=a2-2ab-2ac+b2+2bc+c2
解：原式=[(x+2y)-1][(x+2y)+1]
=x2+4xy+y2-1
=(x+2y)2-12
解：原式=[2x+(y-1)][2x-(y-1)]
=4x2-(y-1)2
=4x2-y2+2y-1
2. 运用乘法公式计算：（3x-2)2 -(2x + 5)2.
原式=[(3x-2)+(2x+5)][(3x-2)-(2x+5)]
=(3x-2+2x+5)(3x-2-2x-5)
=(5x+3)(x-7)
=5x2-35x+3x-21
=5x2-32x-21
原式=9x2-2﹒3x﹒2+4-（4x2+2﹒2x﹒5+25）
=9x2-12x+4-4x2-20x-25
3. 若n是整数，则(n+3)2 -（5n+9）一定能被2整除. 试说明理由.
解：(n+3)2 -（5n+9)=n2+6n+9-5n-9
又∵n(n+1)=n2+n
∴(n+3)2=n(n+1)
∴n(n+1)表示两个连续整数相乘，
∴n(n+1)一定是个偶数，
∴(n+3)2 -（5n+9)一定是个偶数，即一定能被2整除。
运用乘法公式进行计算和推理
互为相反数的平方相等：
个数是5的两位数的平方：
课堂作业：P22习题2第3、4题
课后作业：P22习题2第6、7题，并做P24~26《复习题1》