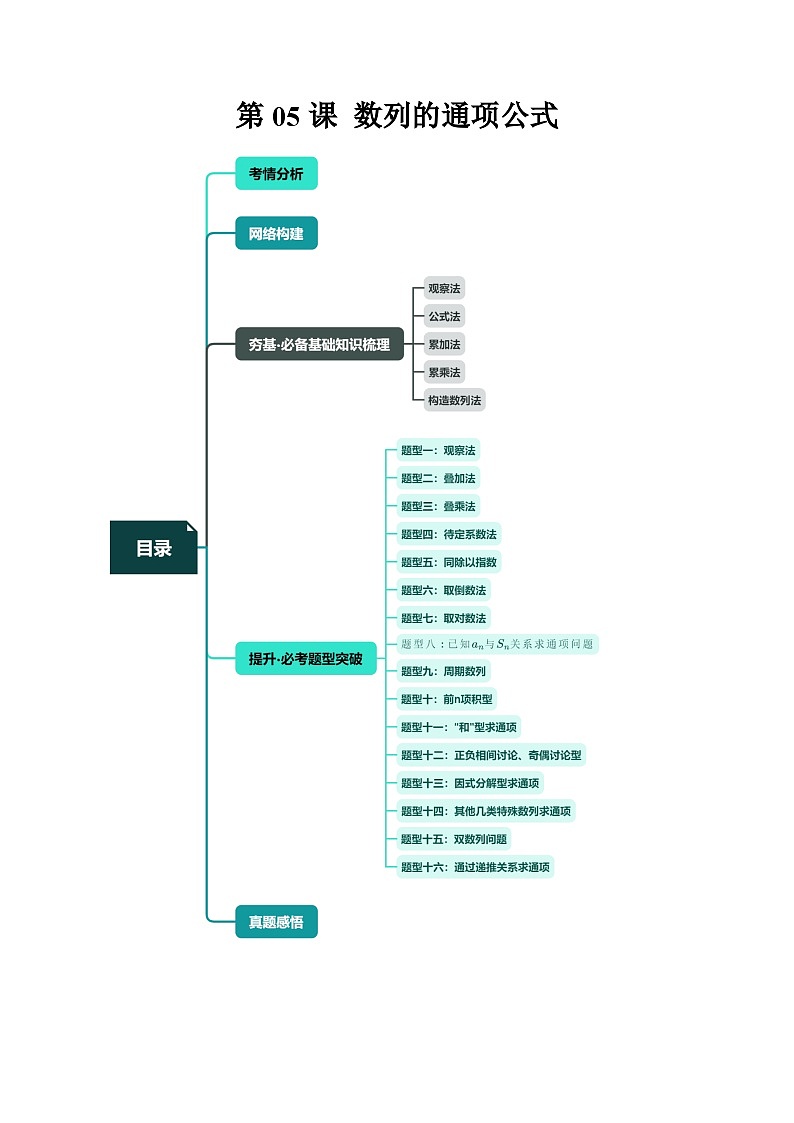
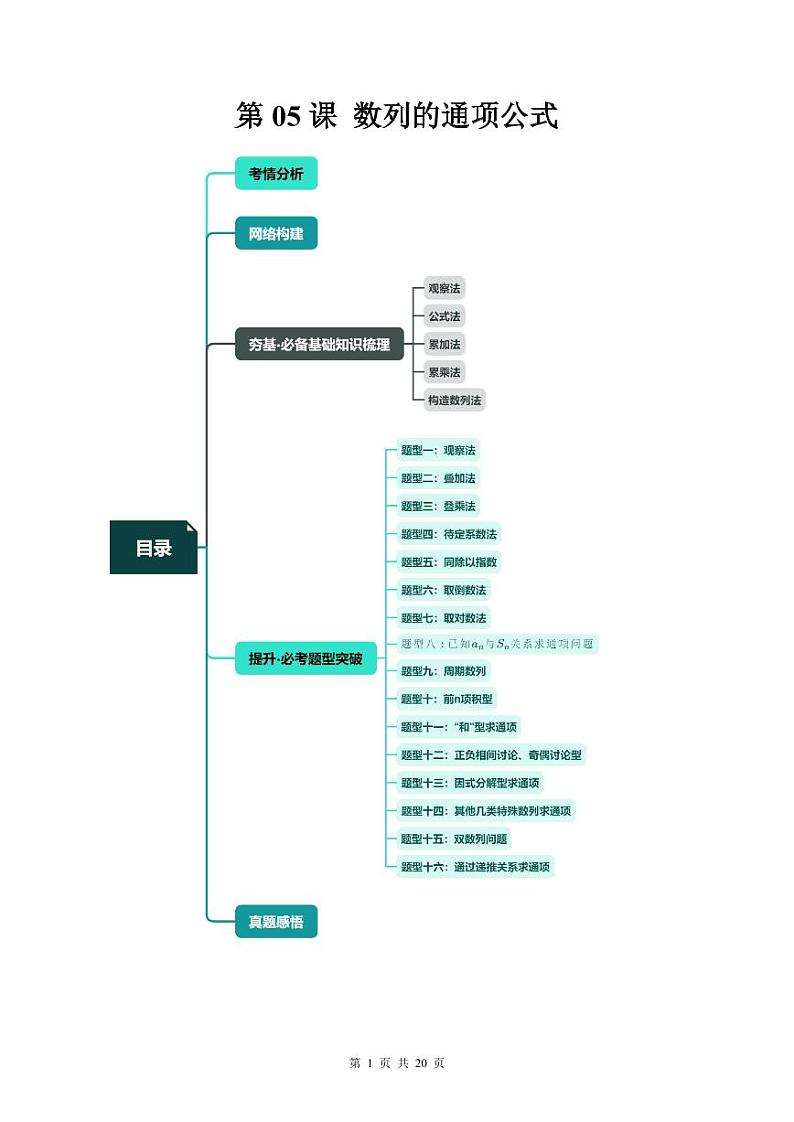
（寒假）2024-2025学年高二数学寒假提升讲义+随堂检测 第05课 数列的通项公式（2份，原卷版+教师版）

这是一份（寒假）2024-2025学年高二数学寒假提升讲义+随堂检测 第05课 数列的通项公式（2份，原卷版+教师版），文件包含寒假2024-2025学年高二数学寒假提升讲义+随堂检测第05课数列的通项公式原卷版docx、寒假2024-2025学年高二数学寒假提升讲义+随堂检测第05课数列的通项公式原卷版pdf、寒假2024-2025学年高二数学寒假提升讲义+随堂检测第05课数列的通项公式教师版docx、寒假2024-2025学年高二数学寒假提升讲义+随堂检测第05课数列的通项公式教师版pdf等4份试卷配套教学资源，其中试卷共64页， 欢迎下载使用。

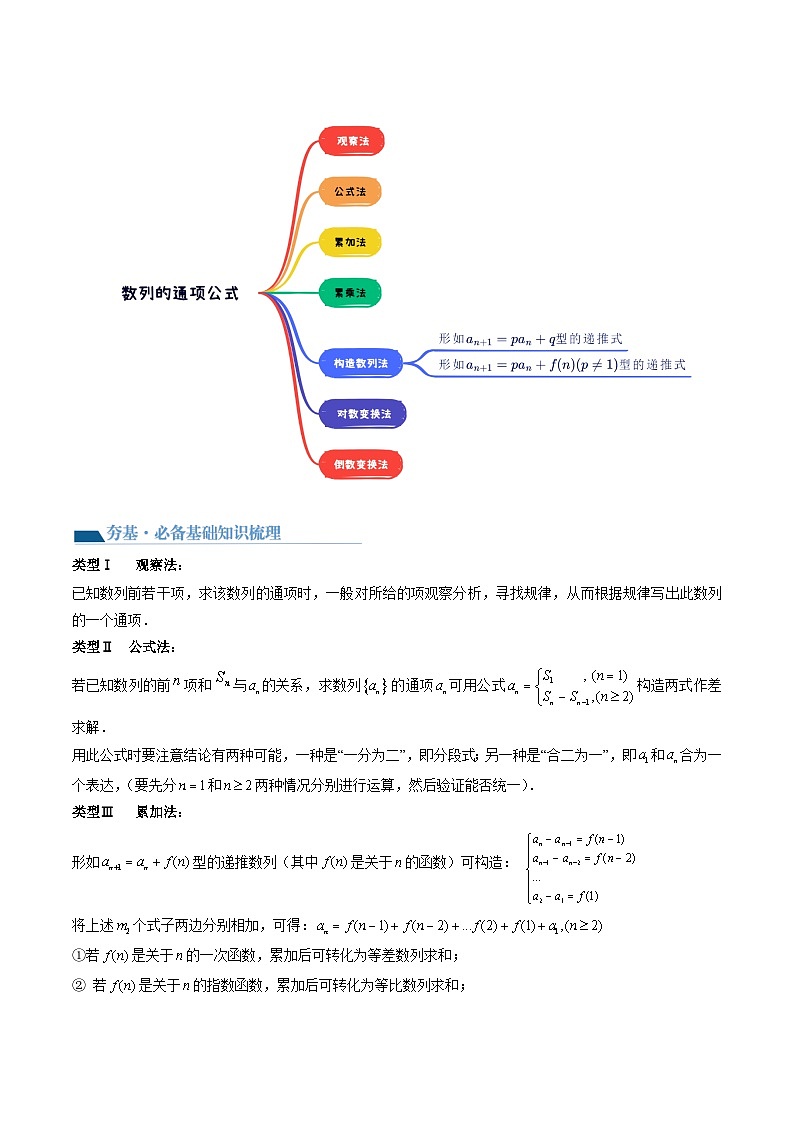
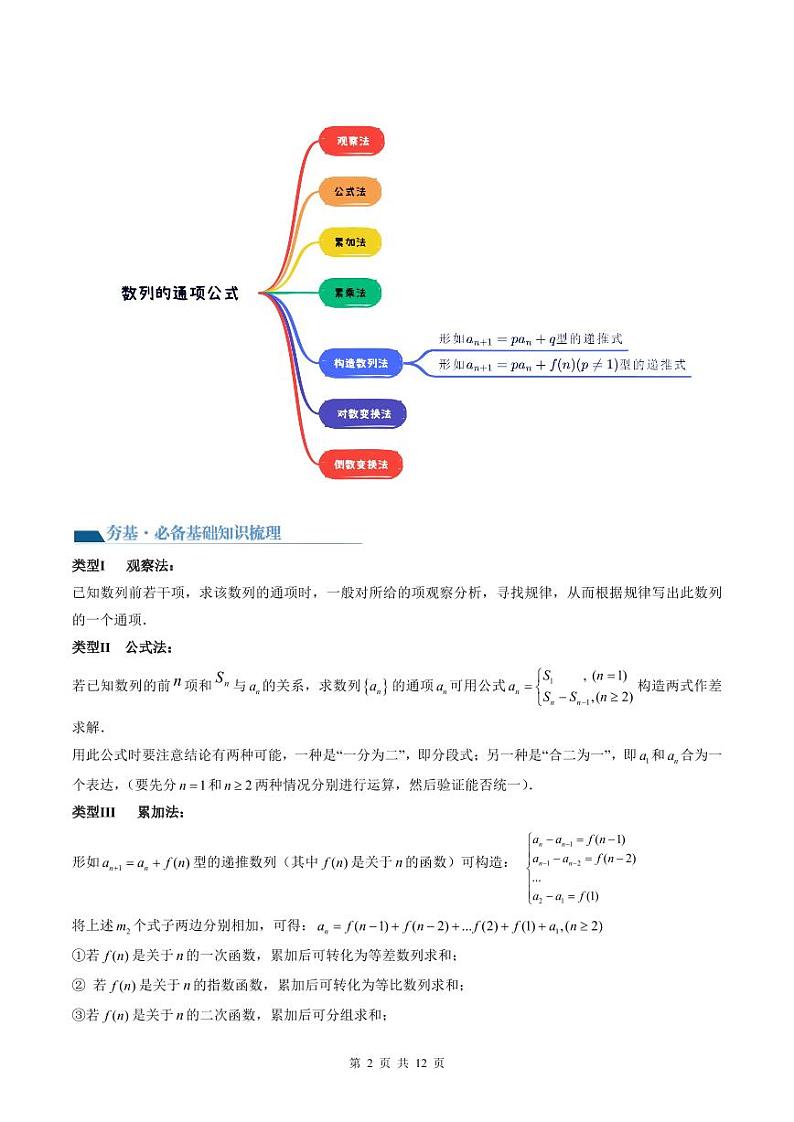
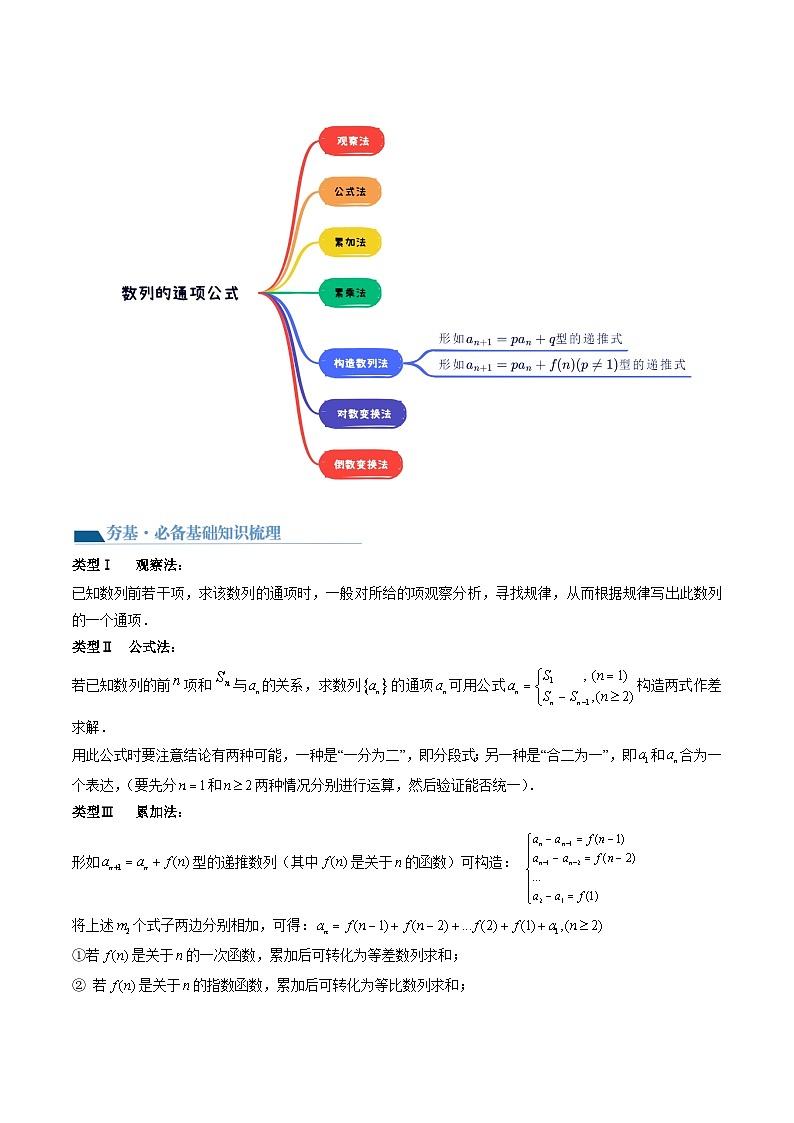
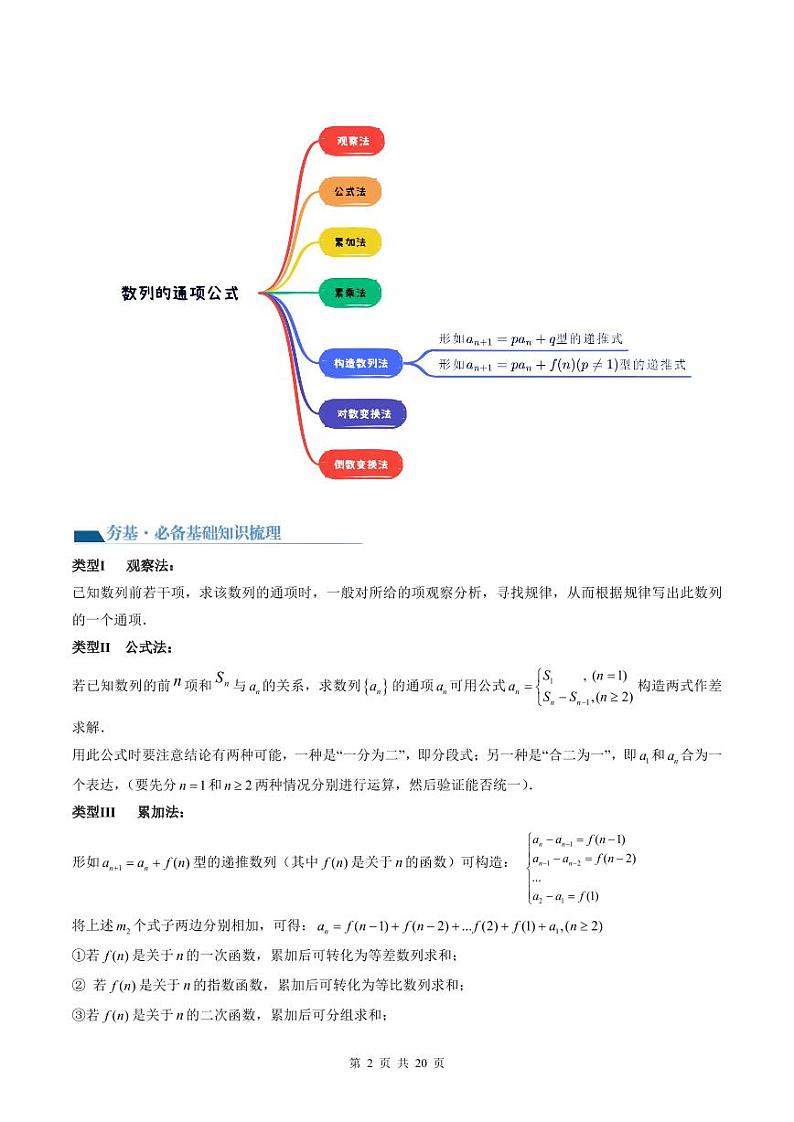
类型Ⅰ 观察法：
已知数列前若干项，求该数列的通项时，一般对所给的项观察分析，寻找规律，从而根据规律写出此数列的一个通项．
类型Ⅱ 公式法：
若已知数列的前项和与的关系，求数列的通项可用公式构造两式作差求解．
用此公式时要注意结论有两种可能，一种是“一分为二”，即分段式；另一种是“合二为一”，即和合为一个表达，（要先分和两种情况分别进行运算，然后验证能否统一）．
类型Ⅲ 累加法：
形如型的递推数列（其中是关于的函数）可构造：
将上述个式子两边分别相加，可得：
= 1 \* GB3 ①若是关于的一次函数，累加后可转化为等差数列求和；
= 2 \* GB3 ② 若是关于的指数函数，累加后可转化为等比数列求和；
= 3 \* GB3 ③若是关于的二次函数，累加后可分组求和；
= 4 \* GB3 ④若是关于的分式函数，累加后可裂项求和．
类型Ⅳ 累乘法：
形如型的递推数列（其中是关于的函数）可构造：
将上述个式子两边分别相乘，可得：
有时若不能直接用，可变形成这种形式，然后用这种方法求解．
类型Ⅴ 构造数列法：
（一）形如（其中均为常数且）型的递推式：
（1）若时，数列{}为等差数列；
（2）若时，数列{}为等比数列；
（3）若且时，数列{}为线性递推数列，其通项可通过待定系数法构造等比数列来求．方法有如下两种：
法一：设，展开移项整理得，与题设比较系数（待定系数法）得，即构成以为首项，以为公比的等比数列．再利用等比数列的通项公式求出的通项整理可得
法二：由得两式相减并整理得即构成以为首项，以为公比的等比数列．求出的通项再转化为类型Ⅲ（累加法）便可求出
（二）形如型的递推式：
（1）当为一次函数类型（即等差数列）时：
法一：设，通过待定系数法确定的值，转化成以为首项，以为公比的等比数列，再利用等比数列的通项公式求出的通项整理可得
法二：当的公差为时，由递推式得：，两式相减得：，令得：转化为类型Ⅴ㈠求出 ，再用类型Ⅲ（累加法）便可求出
（2）当为指数函数类型（即等比数列）时：
法一：设，通过待定系数法确定的值，转化成以为首项，以为公比的等比数列，再利用等比数列的通项公式求出的通项整理可得
法二：当的公比为时，由递推式得：——①，，两边同时乘以得——②，由①②两式相减得，即，在转化为类型Ⅴ㈠便可求出
法三：递推公式为（其中p，q均为常数）或（其中p，q， r均为常数）时，要先在原递推公式两边同时除以，得：，引入辅助数列（其中），得：再应用类型Ⅴ㈠的方法解决．
（3）当为任意数列时，可用通法：
在两边同时除以可得到，令，则，在转化为类型Ⅲ（累加法），求出之后得．
类型Ⅵ 对数变换法：
形如型的递推式：
在原递推式两边取对数得，令得：，化归为型，求出之后得（注意：底数不一定要取10，可根据题意选择）．
类型Ⅶ 倒数变换法：
形如（为常数且）的递推式：两边同除于，转化为形式，化归为型求出的表达式，再求；
还有形如的递推式，也可采用取倒数方法转化成形式，化归为型求出的表达式，再求．
类型Ⅷ 形如型的递推式：
用待定系数法，化为特殊数列的形式求解．方法为：设，比较系数得，可解得，于是是公比为的等比数列，这样就化归为型．
总之，求数列通项公式可根据数列特点采用以上不同方法求解，对不能转化为以上方法求解的数列，可用归纳、猜想、证明方法求出数列通项公式
题型一：观察法
例1．“中国剩余定理”又称“孙子定理”，1852年英国来华传教伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年，英国数学家马西森指出此法符合1801年由高斯得出的关于同余式解法的一般性定理，因而西方称之为“中国剩余定理”．“中国剩余定理”讲的是一个关于整除的问题，现有这样一个整除问题：将正整数中能被3除余2且被7除余2的数按由小到大的顺序排成一列，构成数列，则（ ）
A．17B．37C．107D．128
【答案】C
【解析】∵能被3除余2且被7除余2，∴既是3的倍数，又是7的倍数，
即是21的倍数，且，∴，即，∴．故选：C．
例2．线性分形又称为自相似分形，其图形的结构在几何变换下具有不变性，通过不断迭代生成无限精细的结构.一个正六边形的线性分形图如下图所示，若图1中正六边形的边长为1，图中正六边形的个数记为，所有正六边形的周长之和､面积之和分别记为，其中图中每个正六边形的边长是图中每个正六边形边长的，则下列说法正确的是（ ）
A．B．
C．存在正数，使得恒成立D．
【答案】D
【解析】A选项，图1中正六边形的个数为1，图2中正六边形的个数为7，由题意得为公比为7的等比数列，所以，故，A错误；B选项，由题意知，，，B错误；C选项，为等比数列，公比为，首项为6，故，因为，所以单调递增，不存在正数，使得恒成立，C错误；D选项，分析可得，图n中的小正六边形的个数为个，每个小正六边形的边长为，故每个小正六边形的面积为，则，D正确.故选：D
变式1．大衍数列，来源于《乾坤谱》中对易传“大衍之数五十”的推论，主要用于解释中国传统文化中的太极衍生原理，数列中的每一项都代表太极衍生过程，是中华传统文化中隐藏着的世界数学史上第一道数列题，其各项规律如下：0，2，4，8，12，18，24，32，40，50，．．．，记此数列为，则（ ）
A．650B．1050C．2550D．5050
【答案】A
【解析】由条件观察可得：，即，所以是以2为首项，2为公差的等差数列.故，故选：A
变式2．大衍数列，来源于《乾坤谱》中对易传“大衍之数五十”的推论，主要用于解释中国传统文化中的太极衍生原理，数列中的每一项，都代表太极衍生过程中，曾经经历过的两仪数量总和，是中华传统文化中隐藏着的世界数学史上第一道数列题．其前10项依次是0，2，4，8，12，18，24，32，40，50，则此数列的第25项与第24项的差为（ ）
A．22B．24C．25D．26
【答案】B
【解析】设该数列为，当为奇数时，所以为奇数；当为偶数时，所以为偶数数；所以，故选:B.
变式3．“杨辉三角”是中国古代重要的数学成就，如图是由“杨辉三角”拓展而成的三角形数阵，从第三行起，每一行的第三个数1，，，，构成数列，其前n项和为，则（ ）
A．B．C．D．
【答案】B
【解析】由题意可知，
则，
所以其前n项和为：
，则.故选：B.
【解题方法总结】
观察法即根据所给的一列数、式、图形等，通过观察分析数列各项的变化规律，求其通项．使用观察法时要注意： = 1 \* GB3 \* MERGEFORMAT ①观察数列各项符号的变化，考虑通项公式中是否有或者 部分． = 2 \* GB3 \* MERGEFORMAT ②考虑各项的变化规律与序号的关系． = 3 \* GB3 \* MERGEFORMAT ③应特别注意自然数列、正奇数列、正偶数列、自然数的平方、与有关的数列、等差数列、等比数列以及由它们组成的数列．
题型二：叠加法
例3．数列1，3，7，15，……的一个通项公式是（ ）
A．B．C．D．
【答案】C
【解析】依题意得，，，所以依此类推得，
所以．
又也符合上式，所以符合题意的一个通项公式是．故选：C．
例4．在数列中，，，则（ ）
A．B．C．D．
【答案】B
【解析】因为，故可得，，…，，及累加可得，
则，所以，
则．
故选：B．
变式3．已知数列满足，，则的通项为( )
A． B． C． D．
【答案】D
【解析】因为，所以，则当时，，
将个式子相加可得，因为，则，当时，符合题意，所以.故选：D.
变式4．已知数列 满足：，，，则（ ）
A． B． C． D．
【答案】C
【解析】，，∴，，
∴，
又，故，所以，
所以，
故，
则，所以.故选：C．
【解题方法总结】
数列有形如的递推公式，且的和可求，则变形为，利用叠加法求和
题型三：叠乘法
例5．已知数列满足，，则（ ）
A．2023B．2024C．4045D．4047
【答案】C
【解析】，，即，可得，
.
例6．已知数列满足，(，)，则数列的通项（ ）
A． B． C． D．
【答案】A
【解析】数列满足，，整理得，，，，
所有的项相乘得：，整理得：，故选：．
【解题方法总结】
数列有形如的递推公式，且的积可求，则将递推公式变形为，利用叠乘法求出通项公式
题型四：待定系数法
例7．已知数列是首项为.
(1)求通项公式；
(2)求数列的前项和.
【解析】（1），设，
即，即，解得，
，故是首项为，公比为的等比数列.
，故.
（2），则
.
例8．已知数列中，，满足，设为数列的前项和．
(1)证明：数列是等比数列；
(2)若不等式对任意正整数恒成立，求实数的取值范围．
【解析】（1）因为，所以，
所以是以为首项，公比为的等比数列，
所以，所以．
（2）因为，
所以
，
若对于恒成立，即，
可得即对于任意正整数恒成立，
所以，令，则，
所以，可得，所以，
所以的取值范围为．
变式5．（2023·全国·高三专题练习）已知数列中，，，则数列的通项公式为 .
【答案】
【解析】因为，设，即，根据对应项系数相等则，解得，故，所以是为首项，为公比的等比数列，所以，即.
故答案为：
变式6．已知数列中，，且（，且），则数列的通项公式为 ．
【答案】
【解析】由，得，即由所以，
于是数列是以首项为，公比为的等比数列，因此，即，
当时，,此式满足，所以数列的通项公式为.
故答案为：.
【解题方法总结】
形如（为常数，且）的递推式，可构造，转化为等比数列求解．也可以与类比式作差，由，构造为等比数列，然后利用叠加法求通项．
题型五：同除以指数
例9．已知数列满足，，求数列的通项公式．
【解析】将两边除以，
得，则，故数列是以为首项，以为公差的等差数列，
则，∴数列的通项公式为．
例10．在数列{}中，求通项公式．
【解析】可化为：．
又则数列是首项为，公比是2的等比数列．
∴，则．所以数列{}通项公式为
变式7．已知数列满足，求数列的通项公式．
【解析】由，可得
又，则数列是以为首项，2为公比的等比数列，
则，故．则数列的通项公式为.
变式8．已知数列满足，，求数列的通项公式．
【解析】解法一：因为，设，
所以，
则，解得，即，
则数列是首项为，公比为的等比数列，
所以，即；
解法二：因为，两边同时除以得，
所以，，所以是以为首项，为公比的等比数列，
所以，则，所以.
变式9．已知数列满足，则数列的通项公式为 .
【答案】
【解析】解法一：设，整理得，可得，
即，且，
则数列是首项为，公比为的等比数列，所以，即；
解法二：(两边同除以) 两边同时除以得：，
整理得，且，则数列是首项为，公比为的等比数列，
所以，即；
解法三：(两边同除以)两边同时除以得：，即，
当时，则
，故，
显然当时，符合上式，故.故答案为：.
【解题方法总结】
形如 ，）的递推式，当时，两边同除以转化为关于的等差数列；当时，两边人可以同除以得，转化为．
题型六：取倒数法
例11．设，数列满足，，求数列的通项公式．
【解析】，，两边取倒数得到，
令，则，当时，，，，
数列是首项为，公差为的等差数列．，，．
当时，，则，
数列是以为首项，为公比的等比数列．
，，，
，，
例12．已知数列中，，.
(1)求数列的通项公式；
(2)求证：数列的前n项和.
【解析】（1）因为，，故，
所以，整理得．
又，，，所以为定值，
故数列是首项为2，公比为2的等比数列，所以，得.
（2）因为， 所以．
【解题方法总结】
对于，取倒数得．
当时，数列是等差数列；
当时，令，则，可用待定系数法求解．
题型七：取对数法
例13．已知数列满足，.
(1)证明数列是等比数列，并求数列的通项公式；
(2)若，数列的前项和，求证：.
【解析】（1）因为，所以，则，
又，所以数列是以为首项，为公比的等比数列，
则，所以；
（2）由，得，则，
所以，所以，
所以，
因为，所以，
所以.
【解题方法总结】
形如的递推公式，则常常两边取对数转化为等比数列求解．
题型八：已知通项公式与前项的和关系求通项问题
例14．数列的前项和为，满足，且，则的通项公式是 ．
【答案】
【解析】，，且，
，是以为首项，为公比的等比数列．，．
时，，且不满足上式，所以．
故答案为：.
例15．已知数列中，，前n项和为.若，则数列的前2023项和为 .
【答案】
【解析】在数列中，又，且，
两式相除得，，
∴数列 是以1为首项，公差为1的等差数列，则，∴ ，
当，，当时，，也满足上式，
∴数列的通项公式为，则，
数列的前2023项和为.
故答案为：
变式10．已知各项均为正数的数列满足，其中是数列的前n项和.
(1)求数列的通项公式；
(2)若对任意，且当时，总有恒成立，求实数的取值范围.
【解析】（1）∵，∴当时，，解得.
当时，，即，
∵，∴，∴数列是以1为首项，2为公差的等差数列，∴.
（2）因为，所以
∴当时， ，
∴
，
∴，
∴实数的取值范围为.
变式11．已知是各项都为正数的数列，为其前n项和，且，，
(1)求数列的通项；
(2)证明：.
【解析】（1）法一：因为，所以当时，，
所以，，两式相减可得，
又，所以是首项为，公差为的等差数列，所以，即，
故当时，，经检验，当时，满足上式，
所以.
法二：因为，所以当时，，
故，等号两边平方得，
设，则，
又，，所以是首项为，公差为的等差数列，
故，即，则，
故，则，解得或，
当时，，则，而，矛盾，舍去，
当时，经检验，满足题意，故.
（2）由法一易知，由法二易得，
故由（1）得，，
所以，命题得证.
【解题方法总结】
对于给出关于与的关系式的问题，解决方法包括两个转化方向，在应用时要合理选择．一个方向是转化为的形式，手段是使用类比作差法，使=（，），故得到数列的相关结论，这种方法适用于数列的前项的和的形式相对独立的情形；另一个方向是将转化为（，），先考虑与的关系式，继而得到数列的相关结论，然后使用代入法或者其他方法求解的问题，这种情形的解决方法称为转化法，适用于数列的前项和的形式不够独立的情况．
简而言之，求解与的问题，方法有二，其一称为类比作差法，实质是转化的形式为的形式，适用于的形式独立的情形，其二称为转化法，实质是转化的形式为的形式，适用于的形式不够独立的情形；不管使用什么方法，都应该注意解题过程中对的范围加以跟踪和注意，一般建议在相关步骤后及时加注的范围．
数列的通项公式 随堂检测
1.南宋数学家杨辉所著的《详解九章算法·商功》中出现了如图所示的形状，后人称为“三角垛”，“三角垛”的最上层有1个球，第二层有3个球，第三层有6个球，······，则第十层有（ ）个球．

A．12B．20C．55D．110
【答案】C
【解析】由题意知：，，，
，所以.故选：C
2.若数列的前4项分别是，则该数列的一个通项公式为（ ）
A．B．C．D．
【答案】D
【解析】因为数列的前4项分别是，正负项交替出现，分子均为1，分母依次增加1，
所以对照四个选项，正确.故选：D
3.若，则（ ）
A．55B．56C．45D．46
【答案】D
【解析】由，得，，，，，
累加得，，当时，上式成立，则，
所以.故选：D.
4.已知是数列的前n项和，且对任意的正整数n，都满足：，若，则（ ）
A．B．C．D．
【答案】A
【解析】当时，由累加法可得：，所以（），又因为，所以（），当时，，符合，所以（），所以，所以．故选：A.
5.数列中，，（为正整数），则的值为（ ）
A．B．C．D．
【答案】A
【解析】因为，所以，
所以，故选：A
6.已知，，则数列的通项公式是（ ）
A．B．C．D．n
【答案】D
【解析】由，得，即，则，，，…，，由累乘法可得，所以，又，符合上式，所以.故选：D．
7.已知数列满足，且，则( )
A．B．C．D．
【答案】D
【解析】数列满足，且，∴，，∴，，，，累乘可得：，可得：．故选：D﹒
8.已知数列的前项和为，且（），
(1)求数列的通项公式；
(2)设，求数列的前项和.
【解析】（1）当时，，
当时，，
故，故数列是以1为首项，2为公比的等比数列，故；
（2）由（1）得，故，
则，
故，
则
9.已知数列的前项和为，．
(1)证明：是等差数列；
(2)求数列的前项积．
【解析】（1）由，得．所以，
即，整理得，上式两边同时除以，得．
又，所以，即，所以是首项为2，公差为1的等差数列．
（2）由（1）知，．所以．
所以．
10.已知数列，为数列的前项和，且满足，．
(1)求的通项公式；
(2)证明：．
【解析】（1）对任意的，
当时，，两式相减．整理得，
当时，，
也满足，从而．
（2）证明：证法一：因为，
所以，．
从而；
证法二：因为，
所以，，证毕.