2022-2023学年四川省成都市龙泉驿区九年级上学期数学期末模拟试题及答案

这是一份2022-2023学年四川省成都市龙泉驿区九年级上学期数学期末模拟试题及答案，共27页。
A．x+1＝0B．2x＞2C．D．x2+1＝5
2．（3分）如图所示几何体的俯视图是（ ）
A．B．C．D．
3．（3分）在一个不透明的口袋中装有2个红球和若干个白球，它们除颜色外其他完全相同．通过多次摸球试验后发现，摸到红球的频率稳定在20%附近，则口袋中白球可能有（ ）
A．5个B．6个C．7个D．8个
4．（3分）下列两个图形一定相似的是（ ）
A．有一个角为110°的两个等腰三角形
B．两个直角三角形
C．有一个角为55°的两个等腰三角形
D．两个矩形
5．（3分）方程（m﹣2）x2﹣4x﹣1＝0有两个不等的实数根，则m的取值范围是（ ）
A．m＞﹣2B．m＜﹣2C．m≤﹣2D．m＞﹣2且m≠2
6．（3分）已知△ABC∽△DEF，S△ABC：S△DEF＝1：4．则它们的周长比为（ ）
A．1：2B．1：4C．2：1D．4：1
7．（3分）某超市2019年的销售利润是100万元，计划到2021年利润要达到144万元，若设每年平均增长率是x%，则可得方程（ ）
A．100（1+x）2＝144B．100（1+x%）2＝144
C．x2＝144D．100x（x+1）＝144
8．（3分）函数y＝kx﹣k与y＝在同一坐标系中的图象可能是（ ）
A．B．
C．D．
二．填空题（共10小题，满分30分，每小题3分）
9．（3分）如果反比例函数y＝（a是常数）的图象在第二、四象限，那么a的取值范围是 ．
10．（3分）已知线段a＝2厘米，c＝4厘米，则线段a和c的比例中项b是 厘米．
11．（3分）如图，在矩形ABCD中，已知AB＝3BC＝6，直线EF分别与AB，CD，AC交于点E，F，O，OA＝OC，若G，H分别为AO，OC的中点，且四边形GEHF是矩形，则AE的长为 ．
12．（3分）如图，D、E分别是△ABC的边AB、AC上的动点，若AE＝3，AC＝8，AB＝6，且△ADE与△ABC相似，则AD的长度是 ．
13．（3分）若（b+d≠0），则＝ ．
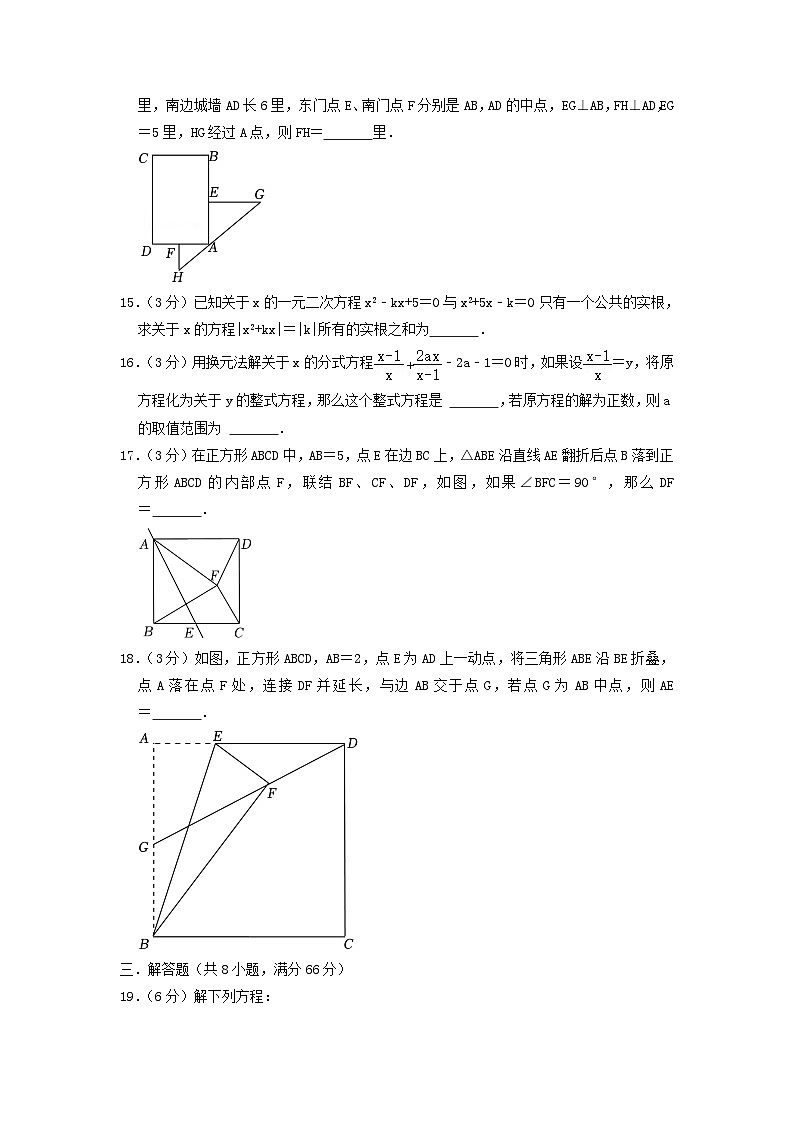
14．（3分）“今有邑，东西六里，南北八里，各开中门，出东门五里有木，问：出南门几何步而见木？”这段话摘自《九章算术》，意思是说：如图，矩形ABCD，东边城墙AB长8里，南边城墙AD长6里，东门点E、南门点F分别是AB，AD的中点，EG⊥AB，FH⊥AD，EG＝5里，HG经过A点，则FH＝ 里．
15．（3分）已知关于x的一元二次方程x2﹣kx+5＝0与x2+5x﹣k＝0只有一个公共的实根，求关于x的方程|x2+kx|＝|k|所有的实根之和为 ．
16．（3分）用换元法解关于x的分式方程﹣2a﹣1＝0时，如果设＝y，将原方程化为关于y的整式方程，那么这个整式方程是 ，若原方程的解为正数，则a的取值范围为 ．
17．（3分）在正方形ABCD中，AB＝5，点E在边BC上，△ABE沿直线AE翻折后点B落到正方形ABCD的内部点F，联结BF、CF、DF，如图，如果∠BFC＝90°，那么DF＝ ．
18．（3分）如图，正方形ABCD，AB＝2，点E为AD上一动点，将三角形ABE沿BE折叠，点A落在点F处，连接DF并延长，与边AB交于点G，若点G为AB中点，则AE＝ ．
三．解答题（共8小题，满分66分）
19．（6分）解下列方程：
（1）2（x﹣1）2﹣18＝0；
（2）2x2﹣7x+3＝0．
20．（8分）如图，点A、F、C、D在同一直线上，点B和点E分别在直线AD的两侧，且AB＝DE，∠A＝∠D，AF＝DC．
（1）求证：四边形BCEF是平行四边形；
（2）若∠DEF＝90°，DE＝8，EF＝6，当AF为 时，四边形BCEF是菱形．
21．（8分）今年猪肉价格受非洲猪瘟疫情影响，有较大幅度的上升，为了解某地区养殖户受非洲猪瘟疫情感染受灾情况，现从该地区建档的养殖户中随机抽取了部分养殖户进行了调查（把调查结果分为四个等级：A级：非常严重；B级：严重；C级：一般；D级：没有感染），并将调查结果绘制成如下两幅不完整的统计图．请根据统计图中的信息解决下列问题：
（1）本次抽样调查的养殖户的总户数是 ；把图2条形统计图补充完整．
（2）若该地区建档的养殖户有1500户，求非常严重与严重的养殖户一共有多少户？
（3）某调研单位想从5户建档养殖户（分别记为a，b，c，d，e）中随机选取两户，进一步跟踪监测病毒传播情况，请用列表或画树状图的方法求出选中养殖户e的概率．
22．（8分）如图，AB和CD表示两根直立于地面的柱子，AD和BC表示起固定作用的两根钢筋，AD与BC的交点记为M，已知AB＝4m，CD＝6m，求点M离地面的高度MH．
23．（8分）图象是函数性质的直观载体，通过图象我们容易把握函数的整体性质，下面我们就一类特殊的函数展开探索，经历分析解析式、列表、描点、连线过程得到函数y＝，y＝+1，y＝﹣1的图象如图所示．
（1）观察发现：三个函数的图象都是双曲线，且分别关于直线y＝x、y＝x+1、y＝x﹣1对称：三个函数解析式中分式部分完全相同，则图象的大小和形状完全相同，只有位置和对称轴发生了变化．因此，我们可以通过描点或平移的方法画函数图象，平移函数y＝的图象可以得到函数y＝+1，y＝﹣1的图象，分别写出平移的方向和距离．
（2）探索思考：在所给的平面直角坐标系中，请用你喜欢的方法画出函数y＝的图象，并写出这个函数的一条性质．
（3）拓展应用：若直线y＝kx+b过点（2，5）、（6，3），结合你所画的函数图象，直接写出不等式≤kx+b的解集．
24．（8分）若y是x的函数，h为常数（h＞0），若对于该函数图象上的任意两点（x1，y1）、（x2，y2），当a≤x1≤b，a≤x2≤b（其中a、b为常数，a＜b）时，总有|y1﹣y2|≤h，就称此函数在a≤x≤b时为有界函数，其中满足条件的所有常数h的最小值，称为该函数在a≤x≤b时的界高．
（1）函数：①y＝2x，②，③y＝x2在﹣1≤x≤1时为有界函数的是 （填序号）；
（2）若一次函数y＝kx+2（k≠0），当a≤x≤b时为有界函数，且在此范围内的界高为b﹣a，请求出此一次函数解析式；
（3）已知函数y＝x2﹣2ax+5（a＞1），当1≤x≤a+1时为有界函数，且此范围内的界高不大于4，求实数a的取值范围．
25．（10分）如图，点A，B在反比例函数y＝（k＞0，x＞0）的图象上，AM⊥x轴于点M，BC∥AM交线段OA于点C，连结OB．已知点A，B的横坐标分别为6，4．
（1）求的值．
（2）当△AOM与△OBC的面积之差等于4时，求k的值．
26．（10分）如图1，在边长为4的正方形ABCD中，点E在直线BC上，连接AE，以AE为边作正方形AEFG（A，E，F，G四个顶点按照逆时针排列），连接AF，直线AF交直线CD于点H．
（1）当点E在边BC上时（点E不与点B重合），连接DG，
①求证：△ADG是直角三角形．
②线段BE，DH，EH之间有怎么的关系，并加以证明．
（2）当点E不在线段BC上时，请直接写出线段BE，DH，EH之间的关系．
（3）如图2，当点E在边BC上时（点E不与点B重合）连接BD，分别交AE，AH于点M，N，当CE+CH＝4.5时，请直接写出线段MN的长．
参考答案与试题解析:
一．选择题（共8小题，满分24分，每小题3分）
1．（3分）下列方程是一元二次方程的是（ ）
A．x+1＝0B．2x＞2C．D．x2+1＝5
【解答】解：A．方程x+1＝0是一元一次方程，选项A不符合题意；
B.2x＞2是一元一次不等式，选项B不符合题意；
C．方程＝4是分式方程，选项C不符合题意；
D．方程x2+1＝5是一元二次方程，选项D符合题意．
故选：D．
2．（3分）如图所示几何体的俯视图是（ ）
A．B．C．D．
【解答】解：根据题意得：该几何体的俯视图为一个矩形，矩形的右侧有一条纵向的线段．
故选：C．
3．（3分）在一个不透明的口袋中装有2个红球和若干个白球，它们除颜色外其他完全相同．通过多次摸球试验后发现，摸到红球的频率稳定在20%附近，则口袋中白球可能有（ ）
A．5个B．6个C．7个D．8个
【解答】解：设袋中白球的个数为x，
根据题意，得：＝20%，
解得x＝8，
经检验x＝8是分式方程的解，
所以口袋中白球可能有8个，
故选：D．
4．（3分）下列两个图形一定相似的是（ ）
A．有一个角为110°的两个等腰三角形
B．两个直角三角形
C．有一个角为55°的两个等腰三角形
D．两个矩形
【解答】解：A、分别有一个角是110°的两个等腰三角形，其底角等于55°，所以有一个角是110°的两个等腰三角形相似，此选项符合题意；
B、两个直角三角形的对应锐角不一定相等，对应边不一定成比例，所以两个直角三角形不一定相似，此选项不符合题意；
C、一个角为55°的两个等腰三角形不一定相似，因为55°的角可能是顶角，也可能是底角，此选项不符合题意；
D、两个矩形的对应边不一定成比例，所以两个矩形不一定相似，此选项不符合题意．
故选：A．
5．（3分）方程（m﹣2）x2﹣4x﹣1＝0有两个不等的实数根，则m的取值范围是（ ）
A．m＞﹣2B．m＜﹣2C．m≤﹣2D．m＞﹣2且m≠2
【解答】解：∵方程（m﹣2）x2﹣4x﹣1＝0有两个不等的实数根，
∴，
解得：m＞﹣2且m≠2．
故选：D．
6．（3分）已知△ABC∽△DEF，S△ABC：S△DEF＝1：4．则它们的周长比为（ ）
A．1：2B．1：4C．2：1D．4：1
【解答】解：∵△ABC∽△DEF，S△ABC：S△DEF＝1：4，
∴△ABC与△DEF的相似比为：1：2，
∴△ABC与△DEF的周长比为：1：2．
故选：A．
7．（3分）某超市2019年的销售利润是100万元，计划到2021年利润要达到144万元，若设每年平均增长率是x%，则可得方程（ ）
A．100（1+x）2＝144B．100（1+x%）2＝144
C．x2＝144D．100x（x+1）＝144
【解答】解：由题意可得，
100（1+x%）＝144，
故选：B．
8．（3分）函数y＝kx﹣k与y＝在同一坐标系中的图象可能是（ ）
A．B．
C．D．
【解答】解：当k＞0时，一次函数y＝kx﹣k的图象过一、三、四象限，反比例函数y＝的图象在二、四象限，
当k＜0时，一次函数y＝kx﹣k的图象过一、二、四象限，反比例函数y＝的图象在一、三象限，
∴A、B、D不符合题意，C符合题意；
故选：C．
二．填空题（共10小题，满分30分，每小题3分）
9．（3分）如果反比例函数y＝（a是常数）的图象在第二、四象限，那么a的取值范围是 a＜2 ．
【解答】解：∵反比例函数y＝的图象分布在第二、四象限，
∴a﹣2＜0，
解得a＜2．
故答案为：a＜2．
10．（3分）已知线段a＝2厘米，c＝4厘米，则线段a和c的比例中项b是 2 厘米．
【解答】解：∵线段b是a、c的比例中项，
∴b2＝ac＝8，
解得b＝±2，
又∵线段是正数，
∴b＝2．
故答案为：2．
11．（3分）如图，在矩形ABCD中，已知AB＝3BC＝6，直线EF分别与AB，CD，AC交于点E，F，O，OA＝OC，若G，H分别为AO，OC的中点，且四边形GEHF是矩形，则AE的长为 3+ ．
解：过O作ON⊥AB于N，
可知，ON＝BC＝1，
∵四边形GFHE是矩形，
∴GH＝EF，
∵G，H分别为OA，OC的中点，
∴OG+OH＝，
在Rt△ABC中，AC＝，
∴OG+OH＝GH＝EF＝，
∴OA＝，OE＝，
在Rt△ONA中，AN＝，
在Rt△ONE中，NE＝，
∴AE＝AN+NE＝3+．
故答案为：3+．
12．（3分）如图，D、E分别是△ABC的边AB、AC上的动点，若AE＝3，AC＝8，AB＝6，且△ADE与△ABC相似，则AD的长度是 4或 ．
解：当△ADE∽△ABC时，可得，
即，
解得AD＝；
当△AED∽△ABC时，可得，
即，
解得AD＝4，
综上所述，AD的长为4或．
故答案为：4或．
13．（3分）若（b+d≠0），则＝ ．
解：∵，
∴a＝b，c＝d，
∴＝．
故答案为：．
14．（3分）“今有邑，东西六里，南北八里，各开中门，出东门五里有木，问：出南门几何步而见木？”这段话摘自《九章算术》，意思是说：如图，矩形ABCD，东边城墙AB长8里，南边城墙AD长6里，东门点E、南门点F分别是AB，AD的中点，EG⊥AB，FH⊥AD，EG＝5里，HG经过A点，则FH＝ 2.4 里．
解：EG⊥AB，FH⊥AD，HG经过A点，
∴FA∥EG，EA∥FH，
∴∠HFA＝∠AEG＝90°，∠FHA＝∠EAG，
∴△GEA∽△AFH，
∴．
∵AB＝8里，DA＝6里，EG＝5里，
∴FA＝3里，EA＝4里，
∴＝，
解得：FH＝2.4里．
故答案为：2.4．
15．（3分）已知关于x的一元二次方程x2﹣kx+5＝0与x2+5x﹣k＝0只有一个公共的实根，求关于x的方程|x2+kx|＝|k|所有的实根之和为 ﹣12 ．
解：设公共根为t，则，
②﹣①得（k+5）t＝k+5，
∵t有唯一的值，
∴k+5≠0，t＝1，
把t＝1代入②得1+5﹣k＝0，解得k＝6，
∴关于x的方程|x2+kx|＝|k|变形为|x2+6x|＝6，
即x2+6x+6＝0或x2+6x﹣6＝0，
∵方程x2+6x+6＝0的两实根之和为﹣6，方程x2+6x﹣6＝0的两实根之和为﹣6，
∴关于x的方程|x2+kx|＝|k|所有的实根之和为﹣12．
故答案为﹣12．
16．（3分）用换元法解关于x的分式方程﹣2a﹣1＝0时，如果设＝y，将原方程化为关于y的整式方程，那么这个整式方程是 y2﹣（2a+1）y+2a＝0 ，若原方程的解为正数，则a的取值范围为 a＜且a≠0 ．
解：设＝y，则＝，关于x的分式方程﹣2a﹣1＝0可化为y+﹣2a﹣1＝0，
两边都乘以y得，y2﹣（2a+1）y+2a＝0，
即（y﹣2a）（y﹣1）＝0，
解得y＝2a（a≠0），y＝1，
当y＝1时，即＝1，此方程无实数根，
当y＝2a时，即＝2a，
两边都乘以x得，x﹣1＝2ax，
解得x＝﹣，
又∵原方程的解为正数，
∴﹣＞0，
解得a＜，而a≠0，
∴a的取值范围为a＜且a≠0，
故答案为：y2﹣（2a+1）y+2a＝0；a＜且a≠0．
17．（3分）在正方形ABCD中，AB＝5，点E在边BC上，△ABE沿直线AE翻折后点B落到正方形ABCD的内部点F，联结BF、CF、DF，如图，如果∠BFC＝90°，那么DF＝ ．
解：连接EF，过点F作FH⊥BC于点H，延长HF交AD于点G，如图所示：
∴∠GHC＝90°，
在正方形ABCD中，∠BCD＝∠CDA＝90°，
∴四边形GHCD是矩形，
∴GH＝CD，GD＝HC，
根据翻折，可得△ABE≌△AFE，
∴∠AFE＝∠ABE，BE＝FE，
∴∠EBF＝∠EFB，
∵∠BFC＝90°，
∴∠FBC+∠FCB＝90°，
∴∠EFC＝∠ECF，
∴FE＝CE，
∴BE＝CE，
在正方形ABCD中，∠ABE＝90°，AB＝BC＝CD＝AD＝5，AD∥BC，
∴∠AFE＝90°，，
∴∠AFG+∠EFH＝90°，
∵∠EFH+∠FEH＝90°，
∴∠AFG＝∠FEH，
∵FH⊥BC，且AD∥BC，
∴∠AGF＝∠FHE＝90°，
∴△AGF∽△FHE，
∴，
设EH＝m，FH＝n，则GF＝2m，AG＝2n，
∵EC＝，
CH＝，
∵GD＝CH，GH＝CD，
∴，
解得，
∴GF＝2m＝3，GD＝＝1，
根据勾股定理，得DF＝＝，
故答案为：．
18．（3分）如图，正方形ABCD，AB＝2，点E为AD上一动点，将三角形ABE沿BE折叠，点A落在点F处，连接DF并延长，与边AB交于点G，若点G为AB中点，则AE＝ ．
解：过点F作MN∥AB，分别交AD，BC于点M，N，如图，
，
∵四边形ABCD为正方形，
∴∠A＝90°，AB＝AD＝2，四边形ABNM为矩形，
∴AM＝BN，AB＝MN＝2，
∵点G为AB中点，
∴＝1，
∵MN∥AB，
∴△DMF∽△DAG，
∴，
即DM＝2MF，
设MF＝x，则DM＝2x，AM＝2﹣2x，NF＝2﹣x，
∴BN＝AM＝2﹣2x，
根据折叠的性质得，AE＝EF，AB＝BF＝2，
在Rt△BNF中，
根据勾股定理得，BF2＝BN2+NF2，
∴22＝（2﹣2x）2+（2﹣x）2，
整理得，5x2﹣12x+4＝0，
解得：或2（舍去），
∴，，
设AE＝y，则EF＝y，EM＝AD﹣DM﹣AE＝2﹣＝，
在Rt△EMF中，
由勾股定理得，EF2＝EM2+MF2，
∴，
∴y＝，
∴AE＝．
故答案为：．
三．解答题（共8小题，满分66分）
19．（6分）解下列方程：
（1）2（x﹣1）2﹣18＝0；
（2）2x2﹣7x+3＝0．
解：（1）（x﹣1）2＝9，
x﹣1＝±3，
所以x1＝4，x2＝﹣2；
（2）（2x﹣1）（x﹣3）＝0，
2x﹣1＝0或x﹣3＝0，
所以x1＝，x2＝3．
20．（8分）如图，点A、F、C、D在同一直线上，点B和点E分别在直线AD的两侧，且AB＝DE，∠A＝∠D，AF＝DC．
（1）求证：四边形BCEF是平行四边形；
（2）若∠DEF＝90°，DE＝8，EF＝6，当AF为 时，四边形BCEF是菱形．
（1）证明：∵AF＝DC，
∴AC＝DF，
在△ABC和△DEF中，
，
∴△ABC≌△DEF（SAS），
∴BC＝EF，∠ACB＝∠DFE，
∴BC∥EF，
∴四边形BCEF是平行四边形；
（2）解：如图，连接BE，交CF于点G，
∵四边形BCEF是平行四边形，
∴当BE⊥CF时，四边形BCEF是菱形，
∵∠DEF＝90°，DE＝8，EF＝6，
∴DF＝＝＝10，
∴FG＝CG＝BC•cs∠BCA＝6×＝，
∴AF＝CD＝DF﹣2FG＝10﹣＝．
故答案为：．
21．（8分）今年猪肉价格受非洲猪瘟疫情影响，有较大幅度的上升，为了解某地区养殖户受非洲猪瘟疫情感染受灾情况，现从该地区建档的养殖户中随机抽取了部分养殖户进行了调查（把调查结果分为四个等级：A级：非常严重；B级：严重；C级：一般；D级：没有感染），并将调查结果绘制成如下两幅不完整的统计图．请根据统计图中的信息解决下列问题：
（1）本次抽样调查的养殖户的总户数是 60 ；把图2条形统计图补充完整．
（2）若该地区建档的养殖户有1500户，求非常严重与严重的养殖户一共有多少户？
（3）某调研单位想从5户建档养殖户（分别记为a，b，c，d，e）中随机选取两户，进一步跟踪监测病毒传播情况，请用列表或画树状图的方法求出选中养殖户e的概率．
解：（1）21÷35%＝60户，60﹣9﹣21﹣9＝21户，
故答案为：60，补全条形统计图如图所示：
（2）1500×＝750户，
答：若该地区建档的养殖户有1500户中非常严重与严重的养殖户一共有750户；
（3）用表格表示所有可能出现的情况如下：
共有20种不同的情况，其中选中e的有8种，
∴P（选中e）＝＝，
22．（8分）如图，AB和CD表示两根直立于地面的柱子，AD和BC表示起固定作用的两根钢筋，AD与BC的交点记为M，已知AB＝4m，CD＝6m，求点M离地面的高度MH．
解：∵AB∥CD，
∴△ABM∽△DCM，
∴＝＝＝，
∵MH∥AB，
∴△MDH∽△ADB，
∴＝＝，
∴＝，
解得MH＝．
故答案为：．
23．（8分）图象是函数性质的直观载体，通过图象我们容易把握函数的整体性质，下面我们就一类特殊的函数展开探索，经历分析解析式、列表、描点、连线过程得到函数y＝，y＝+1，y＝﹣1的图象如图所示．
（1）观察发现：三个函数的图象都是双曲线，且分别关于直线y＝x、y＝x+1、y＝x﹣1对称：三个函数解析式中分式部分完全相同，则图象的大小和形状完全相同，只有位置和对称轴发生了变化．因此，我们可以通过描点或平移的方法画函数图象，平移函数y＝的图象可以得到函数y＝+1，y＝﹣1的图象，分别写出平移的方向和距离．
（2）探索思考：在所给的平面直角坐标系中，请用你喜欢的方法画出函数y＝的图象，并写出这个函数的一条性质．
（3）拓展应用：若直线y＝kx+b过点（2，5）、（6，3），结合你所画的函数图象，直接写出不等式≤kx+b的解集．
解：（1）与相比较，当x相同时，y的值增加1，即函数图象向上平移1个单位长度；与相比较，当x相同时，y的值减小1，即函数图象向下平移1个单位长度；即函数是由函数的图象向上平移一个单位得到；函数的图象是由函数的图象向下平移1个单位长度得到；
（2）函数可变形为，即函数是由函数的图象向上平移2个单位长度得到，并关于直线y＝x+2对称，如图所示：
（3）由函数图象可知，与y＝kx+b都过点（2，5），（6，3），
由函数图象可知，当x＜0或2≤x≤6时，的图象在y＝kx+b的下方，
故不等式≤kx+b的解集为：x＜0或2≤x≤6．
24．（8分）若y是x的函数，h为常数（h＞0），若对于该函数图象上的任意两点（x1，y1）、（x2，y2），当a≤x1≤b，a≤x2≤b（其中a、b为常数，a＜b）时，总有|y1﹣y2|≤h，就称此函数在a≤x≤b时为有界函数，其中满足条件的所有常数h的最小值，称为该函数在a≤x≤b时的界高．
（1）函数：①y＝2x，②，③y＝x2在﹣1≤x≤1时为有界函数的是 ①③ （填序号）；
（2）若一次函数y＝kx+2（k≠0），当a≤x≤b时为有界函数，且在此范围内的界高为b﹣a，请求出此一次函数解析式；
（3）已知函数y＝x2﹣2ax+5（a＞1），当1≤x≤a+1时为有界函数，且此范围内的界高不大于4，求实数a的取值范围．
解：（1）①当x＝﹣1时，y＝﹣2，当x＝1时，y＝2，
∴|y1﹣y2|≤|2﹣（﹣2）|＝4，故y＝2x在﹣1≤x≤1时是有界函数；
②∵的x不等于0，
∴函数在﹣1≤x≤1时没有最大值和最小值，
∴函数在﹣1≤x≤1时不是有界函数；
③当x＝﹣1或x＝1时，y＝1，当x＝0时，y＝0，
∴|y1﹣y2|≤|1﹣0|＝1，故y＝x2在﹣1≤x≤1时是有界函数；
故答案为：①③；
（2）由函数y＝kx+2在a≤x≤b时为有界函数，且此时的界高为b﹣a，
∴y最大值﹣y最小值＝b﹣a，
当k＞0时，y随x的增大而增大，
∴x＝a时，y最小值＝ka+2，x＝b时，y最大值＝kb+2，
∴kb+2﹣（ka+2）＝b﹣a，
∴k＝1，
∴y＝x+2；
当k＜0时，y随x的增大而减小，
∴x＝a时，y最大值＝ka+2，x＝b时，y最小值＝kb+2，
∴ka+2﹣（kb+2）＝b﹣a，
∴k＝﹣1，
∴y＝﹣x+2，
综上所述，一次函数的解析式为y＝x+2或y＝﹣x+2．
（3）∵y＝x2﹣2ax+5＝（x﹣a）2+5﹣a2，a＞1，
∴当1≤x＜a时，y随x的增大而减小，当a＜x≤a+1时，y随x的增大而增大，
∵当1≤x≤a+1时为有界函数，且此范围内的界高不大于4，
∴y最大值﹣y最小值≤4，
当a≤，即1＜a≤2时，a+1离a的距离比1离a的距离远或一样远，
∴x＝a时，y最小值＝5﹣a2，x＝a+1时，y最大值＝（a+1）2﹣2a（a+1）+5＝﹣a2+6，
∴﹣a2+6﹣（5﹣a2）≤4，
化简得：1≤4，
∴1＜a≤2，
当a＞，即a＞2时，a+1离a的距离比1离a的距离近，
∴x＝a时，y最小值＝5﹣a2，x＝1时，y最大值＝1﹣2a+5＝﹣2a+6，
∴﹣2a+6﹣（5﹣a2）≤4，
解得：1＜a≤3，
∴2＜a≤3，
综上所述，a的取值范围为1＜a≤3．
25．（10分）如图，点A，B在反比例函数y＝（k＞0，x＞0）的图象上，AM⊥x轴于点M，BC∥AM交线段OA于点C，连结OB．已知点A，B的横坐标分别为6，4．
（1）求的值．
（2）当△AOM与△OBC的面积之差等于4时，求k的值．
解：（1）延长BC交OM于N，
∵AM⊥x轴，BC∥AM，
∴BN⊥x轴，△CON∽△OAM，
∴＝，
∵A，B的横坐标分别为6，4，
∴OM＝6，ON＝4，
∵点A，B在反比例函数y＝（k＞0，x＞0）的图象上，
∴BN＝，AM＝，
∴＝＝，
∴CN＝AM＝，
∴BC＝BN﹣CN＝﹣＝，
∴＝＝；
（2）∵S△AOM＝•OM•AM＝×6•＝，
S△OBC＝•ON•BC＝×4•＝，
S△AOM﹣S△OBC＝4，
∴﹣＝4，
解得：k＝18．
26．（10分）如图1，在边长为4的正方形ABCD中，点E在直线BC上，连接AE，以AE为边作正方形AEFG（A，E，F，G四个顶点按照逆时针排列），连接AF，直线AF交直线CD于点H．
（1）当点E在边BC上时（点E不与点B重合），连接DG，
①求证：△ADG是直角三角形．
②线段BE，DH，EH之间有怎么的关系，并加以证明．
（2）当点E不在线段BC上时，请直接写出线段BE，DH，EH之间的关系．
（3）如图2，当点E在边BC上时（点E不与点B重合）连接BD，分别交AE，AH于点M，N，当CE+CH＝4.5时，请直接写出线段MN的长．
（1）①证明：∵四边形ABCD和四边形AEFG是正方形，
∴∠ADC＝∠ABE＝∠BAD＝∠EAG＝90°，AB＝AD，AE＝AG，∠GAH＝∠EAH＝∠EAG＝45°，
∴∠BAE＝∠DAG，
在△ADG和△ABE中，，
∴△ADG≌△ABE（SAS），
∴∠ADG＝∠ABE＝90°，
∴△ADG是直角三角形．
②解：BE+DH＝EH，理由如下：
由①得：△ADG≌△ABE，
∴BE＝DG，∠ADG＝∠ABE＝90°，
∴∠ADG+∠ADC＝180°，
∴C、D、G三点共线，
在△AEH和△AGH中，，
∴△AEH≌△AGH（SAS），
∴EH＝GH，
∵GH＝DG+DH＝BE+DH，
∴EH＝BE+DH；
（2）解：当点E在边BC的延长线上时，BE＝DH+EH，理由如下：
如图3所示：
同（1）得：△ADG≌△ABE（SAS），△AEH≌△AGH（SAS），
∴BE＝DG，EH＝GH，
∵DG＝DH+GH＝DH+EH，
∴BE＝DH+EH；
当点E在边CB的延长线上时，DH＝BE+EH，理由如下：
如图4所示：
同（1）得：△ADG≌△ABE（SAS），△AEH≌△AGH（SAS），
∴BE＝DG，EH＝GH，
∵DH＝DG+GH＝BE+EH，
∴DH＝BE+EH；
（3）解：设CE＝x，则BE＝4﹣x，
由（1）得：△ADG≌△ABE（SAS），△AEH≌△AGH（SAS），
∴BE＝DG，EH＝GH，
∵GH＝DG+DH＝BE+DH，
∴EH＝BE+DH，
∴DG＝4﹣x，
∵CE+CH＝4.5，
∴CH＝4.5﹣x，
∴DH＝4﹣（4.5﹣x）＝x﹣0.5，
∴EH＝BE+DH＝4﹣x+x﹣0.5＝3.5＝，
作AO⊥BD于O，如图2所示：
则OA＝BD＝AB＝2，∠BAO＝∠DAO＝45°＝∠EAH，△ABO和△ADO是等腰直角三角形，
∴∠BAE＝∠OAN，∠DAH＝∠OAM，＝＝，
∵∠AON＝∠ABE，
∴△AON∽△ABE，
∴＝＝，
同理：△AOM∽△ADH，
∴＝＝，
∴＝，
又∵∠MAN＝∠HAE，
∴△AMN∽△AHE，
∴＝＝，即＝，
解得：MN＝，
即线段MN的长为．