人教A版 (2019)必修 第二册第六章 平面向量及其应用6.1 平面向量的概念课时作业

这是一份人教A版 (2019)必修 第二册第六章 平面向量及其应用6.1 平面向量的概念课时作业，文件包含61平面向量的概念四大题型精讲原卷版docx、61平面向量的概念四大题型精讲解析版docx等2份试卷配套教学资源，其中试卷共18页， 欢迎下载使用。
TOC \ "1-3" \h \z \u \l "_Tc187247331" 1【本节思维导图】 PAGEREF _Tc187247331 \h 2
\l "_Tc187247332" 2【知识点梳理】 PAGEREF _Tc187247332 \h 2
\l "_Tc187247333" 2.1知识点一：向量的概念 PAGEREF _Tc187247333 \h 2
\l "_Tc187247334" 2.2知识点二：向量的表示法 PAGEREF _Tc187247334 \h 2
\l "_Tc187247335" 2.3知识点三：向量的相关概念 PAGEREF _Tc187247335 \h 3
\l "_Tc187247336" 2.4知识点四：向量的共线或平行 PAGEREF _Tc187247336 \h 3
\l "_Tc187247337" 3【典型例题】 PAGEREF _Tc187247337 \h 3
\l "_Tc187247338" 3.1题型一：向量的基本概念 PAGEREF _Tc187247338 \h 3
\l "_Tc187247339" 3.2题型二：向量的表示方法 PAGEREF _Tc187247339 \h 5
\l "_Tc187247340" 3.3题型三：利用向量相等或共线进行证明 PAGEREF _Tc187247340 \h 7
\l "_Tc187247341" 3.4题型四：向量知识在实际问题中的简单应用 PAGEREF _Tc187247341 \h 9

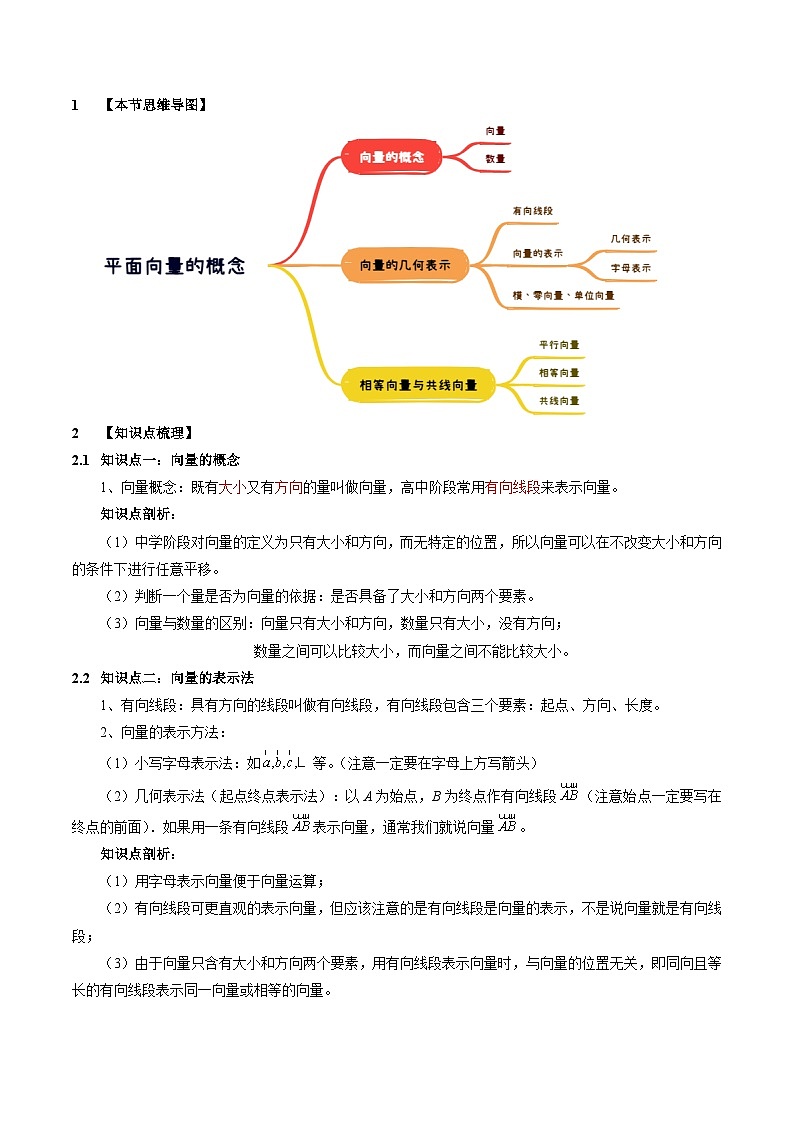
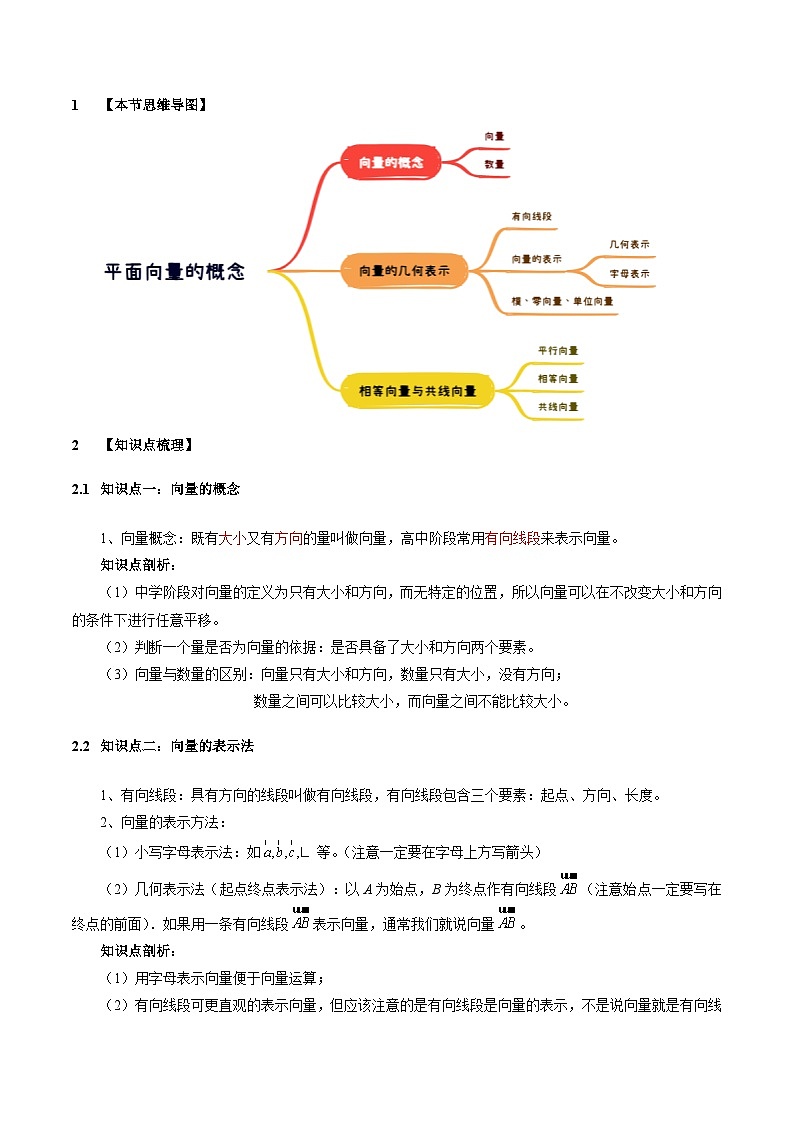
【本节思维导图】
【知识点梳理】
知识点一：向量的概念
1、向量概念：既有大小又有方向的量叫做向量，高中阶段常用有向线段来表示向量。
知识点剖析：
（1）中学阶段对向量的定义为只有大小和方向，而无特定的位置，所以向量可以在不改变大小和方向的条件下进行任意平移。
（2）判断一个量是否为向量的依据：是否具备了大小和方向两个要素。
（3）向量与数量的区别：向量只有大小和方向，数量只有大小，没有方向；
数量之间可以比较大小，而向量之间不能比较大小。
知识点二：向量的表示法
1、有向线段：具有方向的线段叫做有向线段，有向线段包含三个要素：起点、方向、长度。
2、向量的表示方法：
（1）小写字母表示法：如等。（注意一定要在字母上方写箭头）
（2）几何表示法（起点终点表示法）：以A为始点，B为终点作有向线段（注意始点一定要写在终点的前面）．如果用一条有向线段表示向量，通常我们就说向量。
知识点剖析：
（1）用字母表示向量便于向量运算；
（2）有向线段可更直观的表示向量，但应该注意的是有向线段是向量的表示，不是说向量就是有向线段；
（3）由于向量只含有大小和方向两个要素，用有向线段表示向量时，与向量的位置无关，即同向且等长的有向线段表示同一向量或相等的向量。
知识点三：向量的相关概念
1、向量的模：向量的大小叫向量的模（即有向线段的长度）．
知识点剖析：
（1）向量的模；
（2）向量的模是实数。向量不能比较大小，但向量的模是实数，可以比较大小；
2、零向量：长度为零的向量叫零向量。记作，零向量的模长为0，它的方向是任意的；
3、单位向量：长度等于1个单位的向量。
知识点剖析：
（1）在画单位向量时，长度1可以根据需要任意设定；
（2）将一个向量除以它的模，得到的向量就是一个单位向量，并且它的方向与该向量相同。
（3）相等向量：长度相等且方向相同的向量。
知识点剖析：
在平面内，相等的向量有无数多个，它们的方向相同且长度相等，但位置不同。
知识点四：向量的共线或平行
方向相同或相反的非零向量，叫共线向量（共线向量又称为平行向量）．
规定：与任一向量共线．
知识点剖析：
零向量的方向是任意的；
注意与0的含义与书写区别；
向量中平行和共线的意义相同；
共线向量与相等向量的关系：相等向量一定是共线向量，但共线向量不一定是相等的向量。
【典型例题】
题型一：向量的基本概念
【例1】（2024·全国·高一假期作业）下列量中是向量的为（ ）
A．频率B．拉力C．体积D．距离
【答案】B
【解析】显然频率、体积、距离，它们只有大小，不是向量，而拉力既有大小，又有方向，所以拉力是向量.
故选：B
【变式1-1】（2024·安徽阜阳·高二校考阶段练习）下列命题中错误的有（ ）
A．平行向量就是共线向量
B．相反向量就是长度相等且方向相反的向量
C．同向，且，则
D．两个向量平行是这两个向量相等的必要不充分条件
【答案】C
【解析】根据向量的概念，可知A、B正确；
对于C项，向量不能比较大小，故C错误；
对于D项，根据平行向量以及相等向量的概念，可知D正确.
故选：C.
【变式1-2】（2023·广东湛江·高二校考开学考试）下列命题正确的个数是（ ）
（1）向量就是有向线段；（2）零向量是没有方向的向量；
（3）零向量的方向是任意的；（4）零向量的长度为0．
A．1B．2C．3D．4
【答案】B
【解析】（1）向量可以用有向线段表示，但不能把两者等同，故错误；
（2）根据对零向量的规定零向量是有方向的，是任意的，故错误；
（3）根据对零向量的规定，零向量的方向是任意的，故正确；
（4）根据对零向量的规定，零向量的大小为0，所以零向量的长度为0，故正确．
故选：B
【变式1-3】（2024·河南濮阳·高一濮阳一高校考阶段练习）判断下列命题：①两个有共同起点而且相等的非零向量，其终点必相同；②若，则与的方向相同或相反；③若，且，则.其中，正确的命题个数为（ ）
A．0B．1C．2D．3
【答案】B
【解析】相等向量即方向相同大小相等，故两个相同向量同起点比同终点，即①正确；
零向量方向是任意的，且与任意向量都平行，所以当，若，而是非零向量，
则不满足两向量方向相同或相反，即②错误；
同理若，且时，，是非零向量，也得不到，即③错误.
综上正确的是1个.
故选：B
【变式1-4】（2024·高一课时练习）给出下列命题：①两个具有公共终点的向量，一定是共线向量；②两个向量不能比较大小，但它们的模能比较大小；③若 (λ为实数)，则λ必为零；④已知λ，μ为实数，若，则与共线.其中错误命题的个数为（ ）
A．1B．2C．3D．4
【答案】C
【解析】①错误. 两向量共线要看其方向而不是起点与终点.
②正确.因为向量既有大小，又有方向，故它们不能比较大小，但它们的模均为实数，故可以比较大小.
③错误.因为，所以或.
④错误.当λ＝μ＝0时，，此时，与可以是任意向量.
所以错误命题有3个.
故选：C.
题型二：向量的表示方法
【例2】（2024·全国·高一随堂练习）用有向线段表示下列物体运动的速度．
(1)向正东方向匀速行驶的汽车在2h内的位移是60km（用的比例尺）；
(2)做自由落体运动的物体在1s末的速度（用1cm的长度表示速度2m/s）．
【解析】（1），
以为起点，向右作有向线段，它的长度是3cm，
（2），时，，
以为起点，向下作有向线段，长度为：
【变式2-1】（2024·全国·高一随堂练习）用有向线段分别表示一个方向向上、大小为20N的力，以及一个方向向下、大小为30N的力（用1cm的长度表示大小为10N的力）．
【解析】如图，有向线段表示方向向上、大小为20N的力，有向线段表示方向向下、大小为30N的力，
【变式2-2】（2024·全国·高一随堂练习）选择适当的比例尺，用有向线段表示下列向量．
(1)终点A在起点O正东方向3m处；
(2)终点B在起点O正西方向3m处；
(3)终点C在起点O东北方向4m处；
(4)终点D在起点O西南方向2m处．
【解析】（1）从向东作长度为3m的有向线段：
（2）从向西作长度为3m的有向线段：
（3）从点起向北偏东方向作长度为4m的有向线段：
（4）从点起向南偏西方向作长度为2m的有向线段：
题型三：利用向量相等或共线进行证明
【例3】（2024·高一课时练习）如图，和是在各边的三等分点处相交的两个全等的正三角形，设的边长为a，写出图中给出的长度为的所有向量中，
（1）与向量相等的向量；
（2）与向量共线的向量；
（3）与向量平行的向量.
【解析】（1）与向量相等的向量，即与向量大小相等，方向相同的向量，有，；
（2）与向量共线的向量，即与向量方向相同或相反的向量，有，，，，；
（3）与向量平行的向量，即与向量方向相同或相反的向量，有，，，，.
【变式3-1】（2024·全国·高一课堂例题）如图，D，E分别为的边AB，AC的中点，求证：与共线，并用表示．

【解析】证明：因为D，E分别为AB，AC的中点，
所以，
即与共线．
又，且与同向，
所以．
【变式3-2】（2024·全国·高一课堂例题）已知O为正六边形的中心，在图所标出的向量中：

(1)试找出与共线的向量；
(2)确定与相等的向量；
(3)与相等吗？
【解析】（1）由O为正六边形的中心，得与共线的向量有和.
（2）由于与长度相等且方向相同，所以.
（3）显然，且，但与的方向相反，所以这两个向量不相等.
【变式3-3】（2024·高一课时练习）如图所示，在平行四边形中，，分别是，的中点.
(1)写出与向量共线的向量；
(2)求证：.
【解析】（1）因为在平行四边形中，，分别是，的中点，，，
所以四边形为平行四边形，所以.
所以与向量共线的向量为：，，.
（2）证明：在平行四边形中，，.
因为，分别是，的中点，
所以且，
所以四边形是平行四边形，
所以，，
故.
题型四：向量知识在实际问题中的简单应用
【例4】（2024·高一课时练习）一辆汽车从以点出发向西行驶了到达B点，然后向西偏北的方向行驶了到达C点，最后向东行驶了到达D点．
（1）作出向量；
（2）求．
【解析】解:（1）作出向量，如图所示，
（2）作出向量，由题意可知，与方向相反，故与共线，
又，
∴在四边形中，且，
∴四边形为平行四边形，
【变式4-1】（2024·全国·高一随堂练习）如图，某船从点O出发沿北偏东30°的方向行驶至点A处，求该船航行向量的长度（单位：n mile）．

【解析】由题意，
所以向量的长度为2 n mile．
【变式4-2】（2024·高一课时练习）已知飞机从地按北偏东方向飞行到达地，再从地按南偏东方向飞行到达地，再从地按西南方向飞行到达地．画图表示向量，并指出向量的模和方向．
【解析】以为原点，正东方向为轴正方向，正北方向为轴正方向建立直角坐标系．
由题意知点在第一象限，点在x轴正半轴上，点在第四象限，
向量如图所示，
由已知可得，
为正三角形，所以．
又，，
所以为等腰直角三角形，
所以，．
故向量的模为，方向为东南方向．
【变式4-3】（2024·高一课时练习）飞机从A地按北偏西15°的方向飞行到达B地，再从B地按南偏东75°的方向飞行到达C地，那么C地在A地什么方向上？C地距A地多远？
【解析】由题图所示，表示飞机从A地按北偏西15°方向飞行到B地的位移，则.
表示飞机从B地按南偏东75°方向飞行到C地的位移，则.
所以为飞机从A地到C地的位移.
在中，，且，
故为等边三角形，所以，.
所以C地在A地北偏东方向上，距A地.
【变式4-4】（2024·高一课时练习）一名模型赛车手遥控一辆赛车，称先前进1 m，然后原地逆时针转动角为一次操作.
（1）当时，至少需要几次操作，赛车才可以回到出发点？按照适当的比例作图加以说明.
（2）如果，且按此操作，赛车能够回到出发点，那么应该满足什么条件？
【解析】（1）因为
属于至少需要8次操作，赛车可以回到出发点，如图所示.
（2），要使赛车回到出发点，则赛车走过的是一个正多边形路径，考虑外角和为，故每次转动的角度应该是除以一个正整数所得的商，即.