中考数学一轮复习专题11 反比例函数及其应用（10个高频考点）（举一反三）（2份，原卷版+解析版）

这是一份中考数学一轮复习专题11 反比例函数及其应用（10个高频考点）（举一反三）（2份，原卷版+解析版），文件包含中考数学一轮复习专题11反比例函数及其应用10个高频考点举一反三原卷版doc、中考数学一轮复习专题11反比例函数及其应用10个高频考点举一反三解析版doc等2份试卷配套教学资源，其中试卷共81页， 欢迎下载使用。
TOC \ "1-1" \h \u
\l "_Tc25828" 【考点1 反比例函数的定义】 PAGEREF _Tc25828 \h 1
\l "_Tc31524" 【考点2 反比例函数的图象】 PAGEREF _Tc31524 \h 3
\l "_Tc1224" 【考点3 反比例函数图象的对称性】 PAGEREF _Tc1224 \h 9
\l "_Tc6758" 【考点4 反比例函数的性质】 PAGEREF _Tc6758 \h 12
\l "_Tc15071" 【考点5 反比例函数系数k的几何意义】 PAGEREF _Tc15071 \h 14
\l "_Tc2730" 【考点6 反比例函数图象上点的坐标特征】 PAGEREF _Tc2730 \h 18
\l "_Tc18456" 【考点7 待定系数法求反比例函数解析式】 PAGEREF _Tc18456 \h 22
\l "_Tc2062" 【考点8 反比例函数与一次函数的综合】 PAGEREF _Tc2062 \h 29
\l "_Tc9052" 【考点9 实际问题与反比例函数】 PAGEREF _Tc9052 \h 36
\l "_Tc13330" 【考点10 反比例函数与几何综合】 PAGEREF _Tc13330 \h 42
【要点1 反比例函数的定义】
一般的，形如的函数，叫做反比例函数。其中是自变量，是函数。
自变量的取值范围是不等于0的一切实数
【要点2 反比例函数的解析式】
1、； 2、； 3、
【考点1 反比例函数的定义】
【例1】（2022·浙江·校考三模）图像经过点(1，2)的反比例函数是（ ）
A．B．C．D．y＝2x
【答案】B
【分析】将代入到A、B、C函数关系式中求出y值即可找出答案，D中是正比例函数，不用考虑．
【详解】解：观察四个选项，A、B、C是反比函数，D是正比例函数，
将代入到A、B、C函数关系式中，只有B选项中，
故正确答案为：B．
【点睛】本题考查反比例函数上的点，熟练掌握反比例函数的定义是解题关键．
【变式1-1】（2022·辽宁抚顺·统考二模）下列函数中，y是x的反比例函数的是（ ）
A．B．C．D．
【答案】D
【分析】根据反比例函数的定义即形如（k是常数，且k≠0）的函数，对各选项进行判断即可．
【详解】A选项中函数是正比例函数，故不符合题意；
B选项中函数不是反比例函数，故不符合题意；
C选项中函数是正比例函数，故不符合题意；
D选项中函数符合反比例函数的定义，故符合题意；
故选：D．
【点睛】本题考查了反比例函数的定义．解题的关键在于对反比例定义与形式的熟练掌握与灵活运用．
【变式1-2】（2022·北京石景山·统考一模）下列两个变量之间的关系为反比例关系的是（ ）
A．圆的周长与其半径的关系
B．平行四边形面积一定时，其一边长与这边上的高的关系
C．销售单价一定时，销售总价与销售数量的关系
D．汽车匀速行驶过程中，行驶路程与行驶时间的关系
【答案】B
【分析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．
【详解】A. 圆的周长与其半径是正比例关系，不符合题意，
B. 平行四边形面积一定时，其一边长与这边上的高成反比例关系，符合题意，
C. 销售单价一定时，销售总价与销售数量成正比例关系，不符合题意，
D. 汽车匀速行驶过程中，行驶路程与行驶时间成正比例关系，不符合题意，
故选B．
【点睛】本题主要考查成反比例函数关系的量，关键就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．
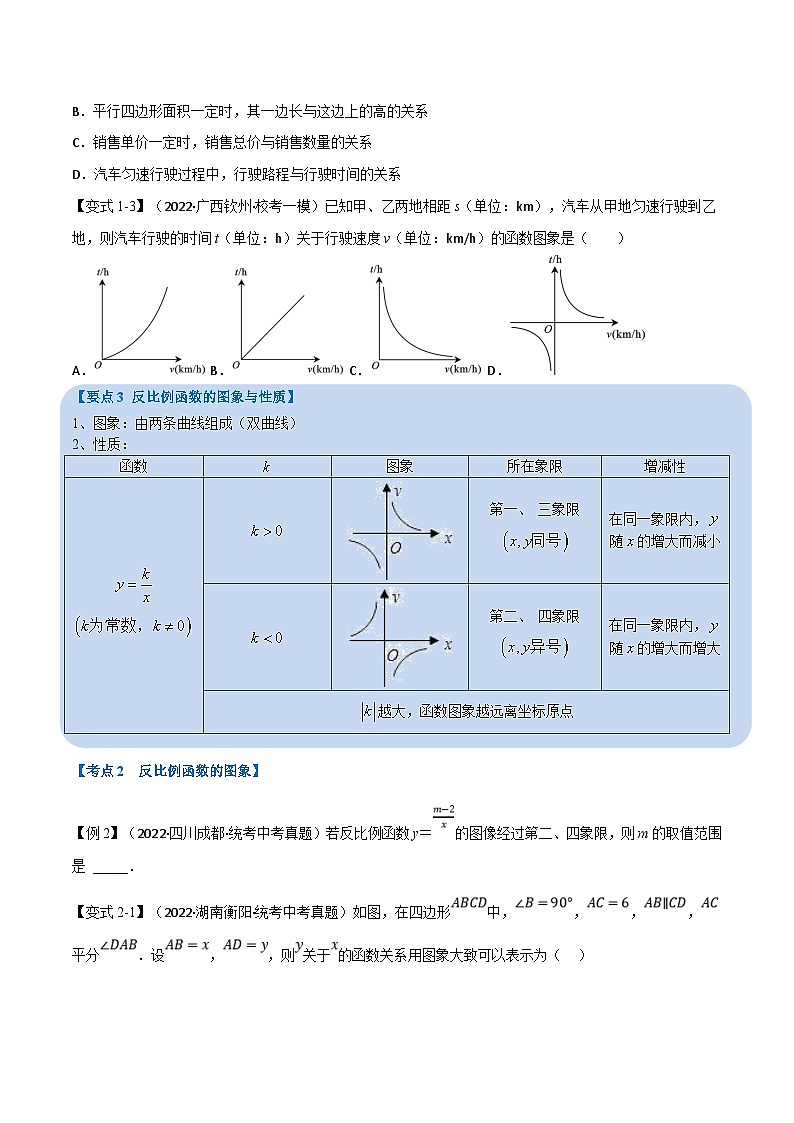
【变式1-3】（2022·广西钦州·校考一模）已知甲、乙两地相距s（单位：km），汽车从甲地匀速行驶到乙地，则汽车行驶的时间t（单位：h）关于行驶速度v（单位：km/h）的函数图象是（ ）
A．B．C．D．
【答案】C
【分析】根据实际意义，写出函数的解析式，根据函数的类型，以及自变量的取值范围即可进行判断．
【详解】解：根据题意有：v•t＝s，
∴，
故t与v之间的函数图象为反比例函数图象，
且根据实际意义v＞0、t＞0，
∴其图像在第一象限，故C正确．
故选：C．
【点睛】本题主要考查了反比例函数的应用，解答该类问题的关键是确定两个变量之间的函数关系，然后利用实际意义确定其所在的象限．
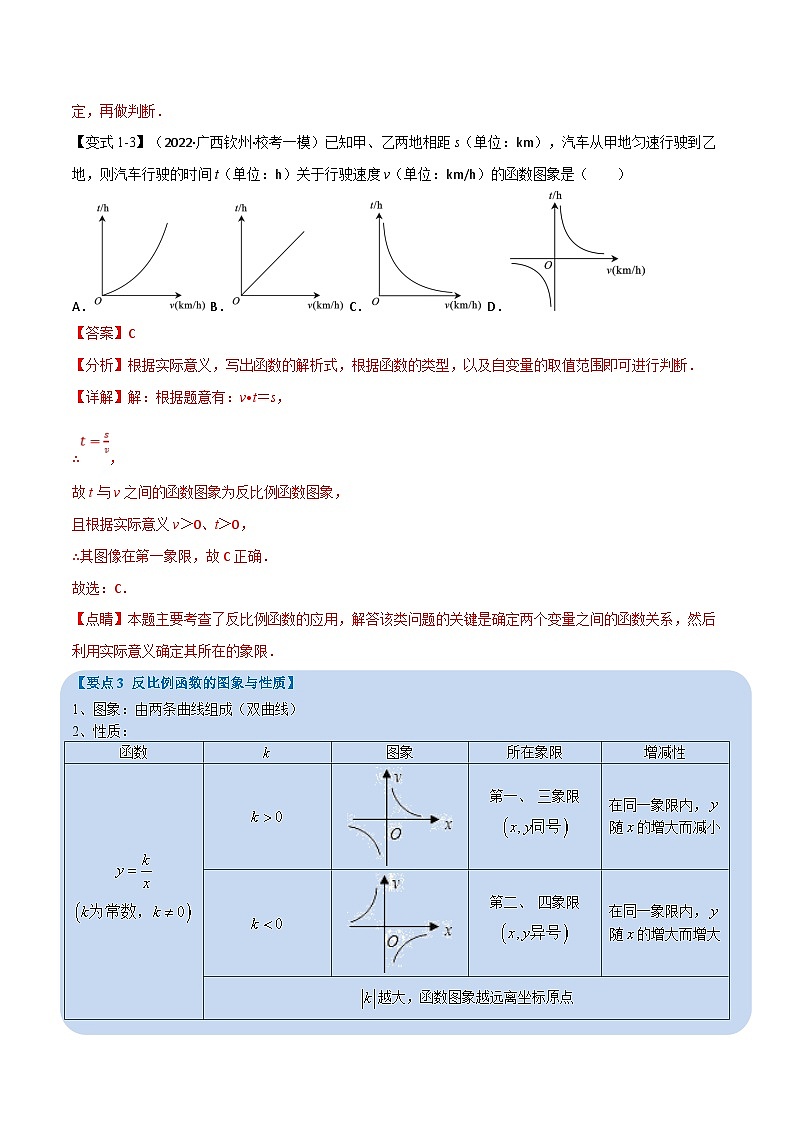
【要点3 反比例函数的图象与性质】
1、图象：由两条曲线组成（双曲线）
2、性质：
【考点2 反比例函数的图象】
【例2】（2022·四川成都·统考中考真题）若反比例函数y＝的图像经过第二、四象限，则m的取值范围是 _____．
【答案】m＜2
【分析】由反比例函数图像经过第二、四象限，得出m﹣2＜0，求出m范围即可．
【详解】解：∵反比例函数y＝的图像经过第二、四象限，
∴m﹣2＜0，
得：m＜2．
故答案为：m＜2．
【点睛】本题主要考查了反比例函数图像的性质，根据反比例函数图像的性质，列出关于m的不等式，是解题的关键．
【变式2-1】（2022·湖南衡阳·统考中考真题）如图，在四边形中，，，，平分．设，，则关于的函数关系用图象大致可以表示为（ ）
B．
C．D．
【答案】D
【分析】先证明，过点做于点，证明，利用相似三角形的性质可得函数关系式，从而可得答案．
【详解】解：∵，∴，
∵平分，∴，
∴，则，即为等腰三角形，
过点做于点．
则垂直平分，，，
∵，，
∴，
∴，
∴，
∴，
∵在中，，
∴，
故选D．
【点睛】本题考查的是角平分线的定义，等腰三角形的判定与性质，相似三角形的判定与性质，反比例函数的图象，证明是解本题的关键．
【变式2-2】（2022·四川雅安·统考中考真题）如图，在平面直角坐标系中，等腰直角三角形ABO的直角顶点A的坐标为（m，2），点B在x轴上，将△ABO向右平移得到△DEF，使点D恰好在反比例函数y＝（x＞0）的图象上．
(1)求m的值和点D的坐标；
(2)求DF所在直线的表达式；
(3)若该反比例函数图象与直线DF的另一交点为点G，求S△EFG．
【答案】(1)
(2)直线的解析式为：
(3)
【分析】（1）如图，过作于 利用等腰直角三角形的性质可得从而可得m的值，再由平移的性质可得D的纵坐标，利用反比例函数的性质可得D的坐标；
（2）由 可得等腰直角三角形向右平移了6个单位，则 再利用待定系数法求解一次函数的解析式即可；
（3）先联立两个函数解析式求解G的坐标，再利用三角形的面积公式进行计算即可．
【详解】（1）解：如图，过作于
为等腰直角三角形，

即
由平移的性质可得：
即
（2）由
等腰直角三角形向右平移了6个单位，

设为
解得：
∴直线的解析式为：
（3）如图，延长FD交反比例函数于G，连结
，
解得： 经检验符合题意；


【点睛】本题考查的是等腰直角三角形的性质，坐标与图形，反比例函数的图象与性质，函数的交点坐标问题，一元二次方程的解法，直角三角形斜边上的中线的性质，熟练是求解G的坐标是解本题的关键．
【变式2-3】（2022·内蒙古包头·中考真题）如图，反比例函数在第一象限的图象上有，两点，直线与x轴相交于点C，D是线段上一点．若，连接，记的面积分别为，则的值为___________．
【答案】4
【分析】如图，连结BD，证明 再求解反比例函数为：， 直线AB为： 再求解 再利用相似三角形的性质可得答案．
【详解】解：如图，连结BD，
，

而

在反比例函数图象上，
即反比例函数为：，
在反比例函数图象上，
即
设直线AB为：
解得：
∴直线AB为：
当时，





故答案为：4
【点睛】本题考查的是反比例函数的图象与性质，相似三角形的判定与 性质，证明是解本题的关键．
【要点4 反比例函数图象的对称性】
（1）中心对称，对称中心是坐标原点
（2）轴对称：对称轴为直线和直线
【考点3 反比例函数图象的对称性】
【例3】（2022·四川攀枝花·统考中考真题）如图，正比例函数与反比例函数的图像交于、B两点，当时，x的取值范围是（ ）
A．或B．或
C．或D．或
【答案】A
【分析】先根据反比例函数图像的对称点求出点的坐标，然后根据的解集即为反比例函数在一次函数上方的部分可得答案．
【详解】解析：正比例函数与反比例函数的图像交于、B两点，
，
由图像可知，当时，x的取值范围是或，
故选：A．
【点睛】本题考查了一次函数与反比例函数的交点问题，根据反比例函数的对称性得出点的坐标的坐标是解本题的关键．
【变式3-1】（2022·四川绵阳·统考二模）下列函数的图象既是轴对称图形，又是中心对称图形的是（ ）
A．y＝x2B．y＝C．y＝|x﹣2|D．y＝
【答案】B
【分析】根据一次函数图象，反比例函数图象，二次函数图象的对称性分析判断即可得解．
【详解】解：A、y＝x2，抛物线是轴对称图形，不是中心对称图形，不符合题意；
B、y＝，反比例函数，图象是双曲线，既是轴对称图形又是中心对称图形，符合题意；
C、y＝|x﹣2|，图象以直线x＝2为对称轴，故不是中心对称图形，不符合题意；
D、y＝，图象以y轴为对称轴，故不是中心对称图形，不符合题意；
故选：B.
【点睛】本题考查了二次函数图象，一次函数图象，反比例函数图象，熟记各图形以及其对称性是解题的关键．
【变式3-2】（2022·山东滨州·阳信县实验中学校考模拟预测）互不重合的两点，皆落于反比例函数图象上，当直线AB与第二象限角平分线垂直时，的值等于（ ）
A．B．1C．D．7
【答案】C
【分析】由直线AB与第二象限角平分线垂直可知A、B关于直线对称，即有，，再根据两点均在反比例函数图象，可得，问题随之得解．
【详解】解：根据题意A、B关于直线对称，
∴，，
∵互不重合的两点，皆落于反比例函数图象上，
∴，
∴，
故选：C．
【点睛】本题主要考考查了反比例函数的性质，轴对称的性质，根据A、B关于直线对称，得出，，是解答本题的关键．
【变式3-3】（2022·江苏南通·统考中考真题）平面直角坐标系中，已知点是函数图象上的三点.若，则k的值为___________．
【答案】##0.75
【分析】由点A、B、C的坐标可知，m＝n，点B、C关于原点对称，求出直线BC的解析式，不妨设m＞0，如图，过点A作x轴的垂线交BC于D，根据列式求出，进而可得k的值．
【详解】解：∵点是函数图象上的三点，
∴，，
∴m＝n，
∴，，
∴点B、C关于原点对称，
∴设直线BC的解析式为，
代入得：，
解得：，
∴直线BC的解析式为，
不妨设m＞0，如图，过点A作x轴的垂线交BC于D，
把x＝m代入得：，
∴D（m，），
∴AD＝，
∴，
∴，
∴，
而当m＜0时，同样可得，
故答案为：．
【点睛】本题考查了反比例函数与几何综合，中心对称的性质，待定系数法求函数解析式，熟练掌握反比例函数的图象和性质，学会利用数形结合的数学思想解答是解题的关键．
【考点4 反比例函数的性质】
【例4】（2022·上海·统考中考真题）已知反比例函数y=（k≠0），且在各自象限内，y随x的增大而增大，则下列点可能在这个函数图象上的为（ ）
A．（2，3）B．（-2，3）C．（3，0）D．（-3，0）
【答案】B
【分析】根据反比例函数性质求出k0)上，且AD⊥x轴，CA的延长线交y轴于点E．若S△ABE=，则k=______．
【答案】3
【分析】连接OD、DE，利用同底等高的两个三角形面积相等得到S△ADE= S△ABE=，以及S△ADE=S△ADO=，再利用反比例函数的比例系数k的几何意义求解即可．
【详解】解：连接OD、DE，
∵四边形ABCD是平行四边形，
∴点B、点D到对角线AC的距离相等，
∴S△ADE= S△ABE=，
∵AD⊥x轴，
∴AD∥OE，
∴S△ADE=S△ADO=，
设点D(x，y) ，
∴S△ADO=OA×AD=xy=，
∴k=xy=3．
故答案为：3．
【点睛】本题考查的是反比例系数k的几何意义，涉及到平行四边形的性质及反比例函数图象上点的坐标特点等相关知识，利用同底等高的两个三角形面积相等得到S△ADE= S△ABE是解题的关键．
【考点6 反比例函数图象上点的坐标特征】
【例6】（2022·辽宁阜新·统考中考真题）已知反比例函数的图像经过点，那么该反比例函数图像也一定经过点（ ）
A．B．C．D．
【答案】C
【分析】先把点代入反比例函数的解析式求出的值，再对各选项进行逐一判断即可．
【详解】解：反比例函数的图象经过点，
，
A、，此点不在反比例函数的图象上，故本选项错误；
B、，此点不在反比例函数的图象上，故本选项错误；
C、，此点在反比例函数的图象上，故本选项正确；
D、，此点不在反比例函数的图象上，故本选项错误．
故选：C．
【点睛】本题考查的是反比例函数图象上点的坐标特点，熟知反比例函数中，为定值是解答此题的关键．
【变式6-1】（2022·江苏淮安·统考中考真题）在平面直角坐标系中，将点向下平移5个单位长度得到点，若点恰好在反比例函数的图像上，则的值是______．
【答案】
【分析】将点向下平移5个单位长度得到点，再把点B代入反比例函数，利用待定系数法进行求解即可．
【详解】将点向下平移5个单位长度得到点，则，
∵点恰好在反比例函数的图像上，
∴，
故答案为：．
【点睛】本题考查了坐标与图形变化—平移，待定系数法求反比例函数的解析式，熟练掌握知识点是解题的关键．
【变式6-2】（2022·广东深圳·统考中考真题）如图，已知直角三角形中，，将绕点点旋转至的位置，且在的中点，在反比例函数上，则的值为________________．
【答案】
【分析】连接，作轴于点，根据直角三角形斜边中线的性质和旋转的性质得出是等边三角形，从而得出，即可得出，解直角三角形求得的坐标，进一步求得．
【详解】解：连接，作轴于点，
由题意知，是中点，，，
，
是等边三角形，
，
，，
，
，
，
，
在反比例函数上，
．
故答案为：．
【点睛】本题考查反比例函数图象上点的坐标特征，坐标与图形变化性质，解题的关键是明确题意，利用数形结合的思想解答．
【变式6-3】（2022·湖北武汉·统考中考真题）如图，，，点A，B分别在函数（）和（）的图象上，且点A的坐标为．
(1)求，的值：
(2)若点C，D分在函数（）和（）的图象上，且不与点A，B重合，是否存在点C，D，使得，若存在，请直接出点C，D的坐标：若不存在，请说明理由．
【答案】(1)，
(2)，
【分析】（1）过点A作AE⊥y轴交于点E，过点B作BF⊥y轴交于点F，将点A代入即可求得，证明△AOE≌△BOF，从而求得点B坐标，将点B代入求得；（2）由可得OC=OA=OB=OD，可得C与B关于x轴对称，A与D关于x轴对称即可求得坐标．
【详解】（1）如图，过点A作AE⊥y轴交于点E，过点B作BF⊥y轴交于点F，
∵，
∴∠AOE+∠BOF=90°，
又∵∠AOE+∠EAO=90°，
∴∠BOF=∠EAO，
又∵∠AEO=∠OFB，OA=OB，
∴△AOE≌△BOF（AAS），
∴AE=OF，OE=BF，
∵点A的坐标为，
∴AE=1，OE=4，
∴OF=1，BF=4，
∴B（4，-1），
将点A、B分别代入和，
解得，，；
（2）由（1）得，点A在图象上，点B在图象上，两函数关于x轴对称，
∵，
∴OC=OA=OB=OD，
只需C与B关于x轴对称，A与D关于x轴对称即可，如图所示，
∴点C（4，1），点D（1，-4）．
【点睛】本题考查反比例函数图象上点的坐标特征和全等三角形的判定和性质，熟知反比例函数的性质是解题的关键．
【考点7 待定系数法求反比例函数解析式】
【例7】（2022·山东威海·统考中考真题）正方形ABCD在平面直角坐标系中的位置如图所示，点A的坐标为（2，0），点B的坐标为（0，4）．若反比例函数y＝（k≠0）的图象经过点C，则k的值为 _____．
【答案】24
【分析】过点C作CE⊥y轴，由正方形的性质得出∠CBA=90°，AB=BC，再利用各角之间的关系得出∠CBE=∠BAO，根据全等三角形的判定和性质得出OA=BE=2，OB=CE=4，确定点C的坐标，然后代入函数解析式求解即可．
【详解】解：如图所示，过点C作CE⊥y轴，
∵点B（0，4），A（2，0），
∴OB=4，OA=2，
∵四边形ABCD为正方形，
∴∠CBA=90°，AB=BC，
∴∠CBE+∠ABO=90°，
∵∠BAO+∠ABO=90°，
∴∠CBE=∠BAO，
∵∠CEB=∠BOA=90°，
∴，
∴OA=BE=2，OB=CE=4，
∴OE=OB+BE=6，
∴C（4，6），
将点C代入反比例函数解析式可得：
k=24，
故答案为：24．
【点睛】题目主要考查正方形的性质，全等三角形的判定和性质，反比例函数解析式的确定等，理解题意，综合运用这些知识点是解题关键．
【变式7-1】（2022·山东淄博·统考中考真题）如图，直线y=kx+b与双曲线y=相交于A（1，2），B两点，与x轴相交于点C（4，0）．
(1)分别求直线AC和双曲线对应的函数表达式；
(2)连接OA，OB，求△AOB的面积；
(3)直接写出当x＞0时，关于x的不等式kx+b＞的解集．
【答案】(1)y=x+，y=；
(2)△AOB的面积为；
(3)1