中考数学一轮复习专题22 与圆有关的位置关系（10个高频考点）（举一反三）（2份，原卷版+解析版）

这是一份中考数学一轮复习专题22 与圆有关的位置关系（10个高频考点）（举一反三）（2份，原卷版+解析版），文件包含中考数学一轮复习专题22与圆有关的位置关系10个高频考点举一反三原卷版doc、中考数学一轮复习专题22与圆有关的位置关系10个高频考点举一反三解析版doc等2份试卷配套教学资源，其中试卷共87页， 欢迎下载使用。
TOC \ "1-1" \h \u
\l "_Tc6796" 【考点1 点与圆的位置关系】 PAGEREF _Tc6796 \h 1
\l "_Tc2492" 【考点2 直线与圆的位置关系】 PAGEREF _Tc2492 \h 3
\l "_Tc7970" 【考点3 圆与圆的位置关系】 PAGEREF _Tc7970 \h 4
\l "_Tc14974" 【考点4 切线的判定的综合运用】 PAGEREF _Tc14974 \h 5
\l "_Tc2164" 【考点5 切线的性质的综合运用】 PAGEREF _Tc2164 \h 6
\l "_Tc26213" 【考点6 切线长定理】 PAGEREF _Tc26213 \h 8
\l "_Tc15685" 【考点7 三角形的内切圆】 PAGEREF _Tc15685 \h 10
\l "_Tc19963" 【考点8 直线和圆的位置关系（一次函数）】 PAGEREF _Tc19963 \h 10
\l "_Tc25989" 【考点9 圆的切线的运用（尺规作圆）】 PAGEREF _Tc25989 \h 11
\l "_Tc25812" 【考点10 动圆问题】 PAGEREF _Tc25812 \h 13
【要点1 点与圆的位置关系】
设⊙O的半径为r，点P到圆心的距离为OP=d，则有：
点P在圆外d＞r；
点P在圆上d=r；
点P在圆内d＜r.
【考点1 点与圆的位置关系】
【例1】（2022·吉林·统考中考真题）如图，在中，，，．以点为圆心，为半径作圆，当点在内且点在外时，的值可能是（ ）
A．2B．3C．4D．5
【变式1-1】（2022·广西北海·统考二模）已知的半径为3，，则点A和的位置关系是（ ）
A．点A在圆上B．点A在圆外C．点A在圆内D．不确定
【变式1-2】（2022·山东枣庄·校考一模）设P为外一点，若点P到的最短距离为2，最长距离为6，则的半径为______．
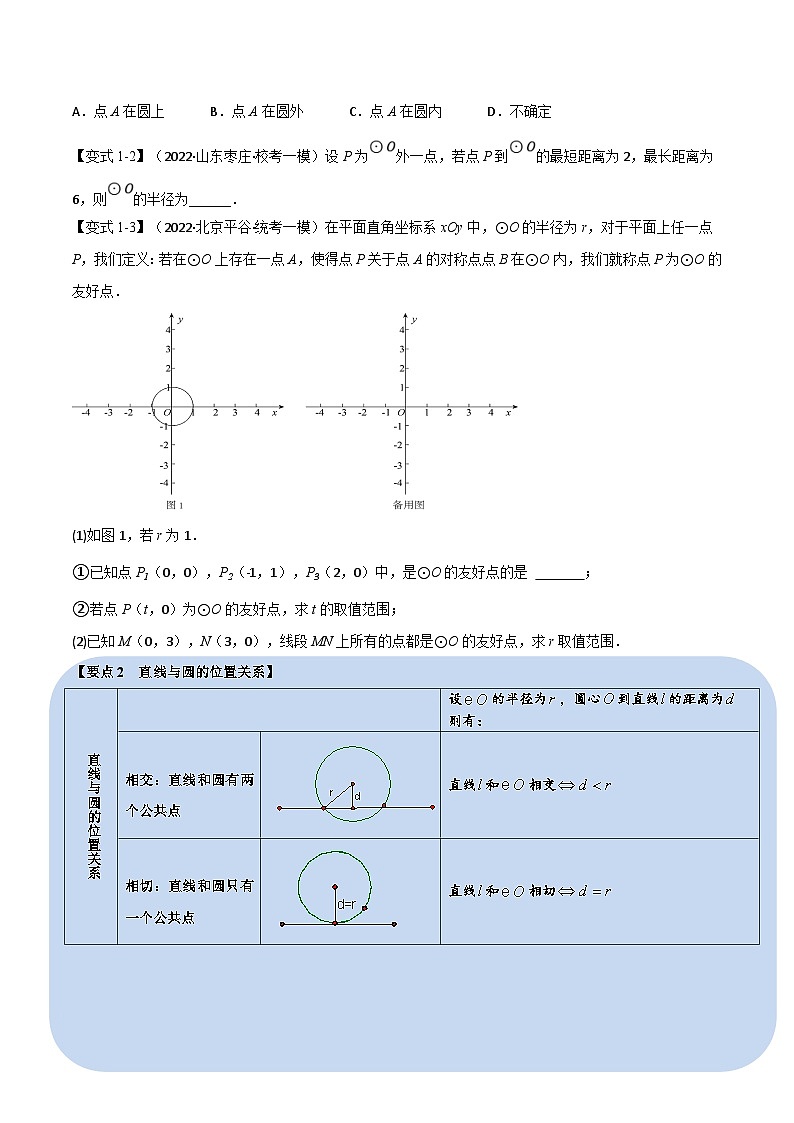
【变式1-3】（2022·北京平谷·统考一模）在平面直角坐标系xOy中，⊙O的半径为r，对于平面上任一点P，我们定义：若在⊙O上存在一点A，使得点P关于点A的对称点点B在⊙O内，我们就称点P为⊙O的友好点．
(1)如图1，若r为1．
①已知点P1（0，0），P2（﹣1，1），P3（2，0）中，是⊙O的友好点的是 ；
②若点P（t，0）为⊙O的友好点，求t的取值范围；
(2)已知M（0，3），N（3，0），线段MN上所有的点都是⊙O的友好点，求r取值范围．
【要点2 直线与圆的位置关系】
【考点2 直线与圆的位置关系】
【例2】（2022·上海金山·统考二模）在直角坐标系中，点P的坐标是(2，)，圆P的半径为2，下列说法正确的是（ ）
A．圆P与x轴有一个公共点，与y轴有两个公共点
B．圆P与x轴有两个公共点，与y轴有一个公共点
C．圆P与x轴、y轴都有两个公共点
D．圆P与x轴、y轴都没有公共点
【变式2-1】（2022·浙江杭州·统考一模）如图，若⊙的半径为6，圆心到一条直线的距离为6，则这条直线可能是（ ）
A．B．C．D．
【变式2-2】（2022·四川乐山·统考模拟预测）如图，点P在抛物线y＝x2﹣3x+1上运动，若以P为圆心的圆与x轴、y轴都相切，则符合上述条件的所有的点P共有（ ）
A．2个B．3个C．4个D．5个
【变式2-3】（2022·上海松江·统考二模）如图，已知中，，．、分别是边、上的点，，且．如果经过点，且与外切，那么与直线的位置关系是（ ）
A．相离B．相切C．相交D．不能确定
【考点3 圆与圆的位置关系】
【例3】（2022·上海松江·校考三模）已知，以点为圆心，以为半径画圆，以点为圆心，半径为，画圆已知与外离，则的取值范围为（ ）
A．0B．0C．0D．0
【变式3-1】（2022·四川绵阳·一模）如图，⊙O1的直径AB长度为12，⊙O2的直径为8，∠AO1O2＝30°，⊙O2沿直线O1O2平移，当⊙O2平移到与⊙O1和AB所在直线都有公共点时，令圆心距O1O2＝x，则x的取值范围是（ ）
A．2≤x≤10B．4≤x≤16C．4≤x≤4D．2≤x≤8
【变式3-2】（2022·湖北武汉·统考模拟预测）如图，点C是OD的中点，以OC为半径作⊙O，以CD为直径作⊙O'，AB与⊙O和⊙O'分别相切于点A和点B，连接BD，则cs∠BDC的值是（ ）
A．B．C．D．
【变式3-3】（2022·上海青浦·统考二模）如图，在直角梯形中，，E是上一定点，．点P是BC上一个动点，以P为圆心，PC为半径作⊙P．若⊙P与以E为圆心，1为半径的⊙E有公共点，且⊙P与线段AD只有一个交点，则PC长度的取值范围是 __．

【要点3 切线的判定】
（1）切线判定： = 1 \* GB3 ①经过半径的外端并且垂直于这条半径的直线是圆的切线
= 2 \* GB3 ②和圆只有一个公共点的直线是圆的切线（定义法）
= 3 \* GB3 ③如果圆心到一条直线的距离等于圆的半径，那么这条直线是圆的切线
（2）切线判定常用的证明方法：
①知道直线和圆有公共点时，连半径，证垂直；
②不知道直线与圆有没有公共点时，作垂直，证垂线段等于半径．
【考点4 切线的判定的综合运用】
【例4】（2022·湖北黄石·统考中考真题）如图是直径，A是上异于C，D的一点，点B是延长线上一点，连接、、，且．
(1)求证：直线是的切线；
(2)若，求的值；
(3)在（2）的条件下，作的平分线交于P，交于E，连接、，若，求的值．
【变式4-1】（2022·西藏·统考中考真题）如图，已知BC为⊙O的直径，点D为的中点，过点D作DG∥CE，交BC的延长线于点A，连接BD，交CE于点F．
(1)求证：AD是⊙O的切线；
(2)若EF＝3，CF＝5，tan∠GDB＝2，求AC的长．
【变式4-2】（2022·宁夏·中考真题）如图，以线段为直径作，交射线于点，平分交于点，过点作直线于点，交的延长线于点．连接并延长交于点．
(1)求证：直线是的切线；
(2)求证：；
(3)若，，求的长．
【变式4-3】（2022·辽宁鞍山·统考中考真题）如图，是的外接圆，为的直径，点为上一点，交的延长线于点，与交于点，连接，若．
(1)求证：是的切线．
(2)若，，求的半径．
【要点4 切线的性质】
（1）切线性质定理：圆的切线垂直于过切点的半径
（2）切线性质的推论： = 1 \* GB3 ①经过圆心且垂直于切线的直线必经过切点
= 2 \* GB3 ②经过切点且垂直于切线的直线必经过圆心
【考点5 切线的性质的综合运用】
【例5】（2022·湖北十堰·统考中考真题）如图，中，，为上一点，以为直径的与相切于点，交于点，，垂足为．
(1)求证：是的切线；
(2)若，，求的长．
【变式5-1】（2022·内蒙古鄂尔多斯·统考中考真题）如图，以AB为直径的⊙O与△ABC的边BC相切于点B，且与AC边交于点D，点E为BC中点，连接DE、BD．
(1)求证：DE是⊙O的切线；
(2)若DE＝5，cs∠ABD＝，求OE的长．
【变式5-2】（2022·湖北随州·统考中考真题）如图，已知D为⊙O上一点，点C在直径BA的延长线上，BE与⊙O相切，交CD的延长线于点E，且．
(1)判断CD与⊙O的位置关系，并说明理由；
(2)若，，
①求⊙O的半径；
②求BD的长．
【变式5-3】（2022·广东东莞·石龙三中校考三模）如图，AB为的直径CE与相切于点D，与BA的延长线交于点E，交CO延长线于点F，连接OD，CB，已知．
(1)求证：CB是的切线；
(2)求的半径；
(3)连接BF，求．
【要点5 切线长定理】
（1）切线长定理：过圆外一点所画的圆的两条切线长相等，这一点和圆心的连线平分两条切线的夹角
【考点6 切线长定理】
【例6】（2022·贵州黔东南·统考中考真题）如图，、分别与相切于点、，连接并延长与交于点、，若，，则的值为（ ）
A．B．C．D．
【变式6-1】（2022·四川眉山·中考真题）如图是不倒翁的主视图，不倒翁的圆形脸恰好与帽子边沿，分别相切于点，，不倒翁的鼻尖正好是圆心，若，则的度数为（ ）
A．B．C．D．
【变式6-2】（2022·四川泸州·校考模拟预测）如图，的内切圆⊙O与，BC，CA分别相切于点D，E，F，，则AD的长是（ ）
A．B．C．D．
【变式6-3】（2022·山东淄博·统考二模）如图，内切于，点P、点Q分别在直角边、斜边上，，且与相切，若，则的值为（ ）
A．B．C．D．
【要点6 三角形的内切圆】
【考点7 三角形的内切圆】
【例7】（2022·四川宜宾·统考中考真题）我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形（如图所示）．若直角三角形的内切圆半径为3，小正方形的面积为49，则大正方形的面积为______．
【变式7-1】（2022·辽宁沈阳·统考一模）已知一个等边三角形的边长是6，那么这个等边三角形内切圆半径是________．
【变式7-2】（2022·四川成都·模拟预测）如图，已知是的内切圆，，BO的延长线交AC于点D，若，，则的半径长为______．
【变式7-3】（2022·湖北武汉·校联考一模）如图，AB＝AC，⊙O是△ABC的内切圆，切点为D、E、F，连接DE、CD交⊙O于G，连接EG并延长交BC于H．
(1)求证：DE∥BC
(2)连接AG，若EH⊥BC求的值；
【考点8 直线和圆的位置关系（一次函数）】
【例8】（2022·山东菏泽·统考三模）已知在直角坐标系中，以点为圆心，以3为半径作，则直线与的位置关系是（ ）
A．相切B．相交C．相离D．与k值有关
【变式8-1】（2022·江苏南京·统考二模）在平面直角坐标系中，以O为圆心，2个单位长度为半径画圆．若一次函数（k为常数，）的图像与有公共点，则k的取值范围是_________．
【变式8-2】（2022·福建龙岩·统考二模）直线与轴、轴分别交于A和B点，圆心为（0，2）且与轴相切的圆上有一动点P，则点P到直线AB的距离的最小值为______．
【变式8-3】（2022秋·江苏扬州·九年级统考阶段练习）已知一次函数y=x+2的图象分别交x轴，y轴于A、B两点，⊙O1过以OB为边长的正方形OBCD的四个顶点，两动点P、Q同时从点A出发在四边形ABCD上运动，其中动点P以每秒个单位长度的速度沿A→B→A运动后停止；动点Q以每秒2个单位长度的速度沿A→O→D→C→B运动，AO1交y轴于E点，P、Q运动的时间为t（秒）．
（1）求E点的坐标和S△ABE的值；
（2）试探究点P、Q从开始运动到停止，直线PQ与⊙O1有哪几种位置关系，并求出对应的运动时间t的范围．
【考点9 圆的切线的运用（尺规作圆）】
【例9】（2022·江苏泰州·校联考三模）如图，AB是⊙O的直径，点D在AB的延长线上，点C在⊙O上，CA＝CD，∠CDA＝30°．
（1）试判断直线CD与⊙O的位置关系，并说明理由；
（2）若⊙O的半径为4，
①用尺规作出点A到CD所在直线的距离；
②求出该距离．
【变式9-1】（2022·山东烟台·统考中考真题）如图，⊙O是△ABC的外接圆，∠ABC＝45°．
(1)请用尺规作出⊙O的切线AD（保留作图痕迹，不写作法）；
(2)在（1）的条件下，若AB与切线AD所夹的锐角为75°，⊙O的半径为2，求BC的长．
【变式9-2】（2022春·湖南·九年级统考期中）如图．△ABC是直角三角形，∠ACB＝90°，∠A＝30°．
(1)实践与操作：利用尺规按下列要求作图．并在图中标明相应字母（保留作图痕迹．不写作法）．
①作△ABC的外接圆O；
②在AB的延长线上作一点D，使得CD与⊙O相切；
(2)综合与运用：在你所作的图中．若AC＝6，则由线段CD、BD及所围成图形的面积为______．
【变式9-3】（2022秋·河南商丘·九年级校考阶段练习）【已有经验】我们通过尺规作图，可以作经过A，B两点，如图1所示；也可以作（或），使（或）过点M，且与直线l相切，如图2－1（或图2－2）．

(1)【迁移经验】用尺规按要求画图：如图3，已知，求作使其与的两边都相切；（保留作图痕迹，不写作法）
(2)【问题解决】如图4，在中，，，．若经过点C，且与直线相切，的半径为r，当圆心O在的内部（含边界）时，
①求r的最小值；
②直接写出r的最大值．
【考点10 动圆问题】
【例10】（2022·上海·二模）如图，直线AB，CD相交于点O，，圆P的半径为1cm，动点P在直线AB上从点O左侧且距离O点6cm处，以1cm/s的速度向右运动，当圆P与直线CD相切时，圆心P的运动时间为 _____s．
【变式10-1】（2022·江苏常州·校联考一模）如图，在平面直角坐标系中，一次函数的图像与轴、轴分别交于点，点从点出发沿射线运动，点在射线上，且，以为直径作，设点．
（1）求线段的长；
（2）当点在轴上方且与轴相切时，求的值；
（3）若直径将分成的两个半圆弧中有一个半圆弧落在的内部时（含角的边上），直接写出的取值范围．
【变式10-2】（2022·河北石家庄·统考二模）如图1和图2，点在数轴上对应的数为16，过原点在数轴的上方作射线，且.点从点出发，沿数轴以每秒2个单位长度的速度向点运动，同时点从点出发，沿方向以每秒1个单位长度的速度运动，当点到达点时，点，都停止运动.以点为圆心，为半径的半圆与数轴正半轴交于点，与射线交于点，连接，设运动时间为秒，点在数轴上对应的数为．
（1）用含的式子表示的长为______，当点与点重合时，______；
（2）若与半圆相切，求；
（3）如图2，当时，半圆与的另一个交点为，求的度数及的长；
（4）若半圆与线段只有一个公共点，直接写出的取值范围．
【变式10-3】（2022春·黑龙江大庆·九年级校考阶段练习）如图，在Rt△ACB中，∠ACB＝90°，AC＝3，BC＝4，有一过点C的动圆O与斜边AB相切于动点P，连接CP．随着切点P的位置不同，则圆O的半径最小值为（ ）
A．2.5B．2.4C．2.2D．1.2直线与圆的位置关系
设的半径为，圆心到直线的距离为
则有：
相交：直线和圆有两个公共点
直线和相交
相切：直线和圆只有一个公共点
直线和相切
相离：直线和圆没有公共点
直线和相离
三角形内切圆
与三角形各边都相切的圆叫做三角形的内切圆
内切圆的圆心是三角形三个内角的角平分线的交点，叫做三角形的内心
三角形的内心到三角形三边的距离相等