中考数学二轮复习几何专项知识精讲+基础提优训练专题01 角平分线模型（知识精讲）

这是一份中考数学二轮复习几何专项知识精讲+基础提优训练专题01 角平分线模型（知识精讲），共6页。
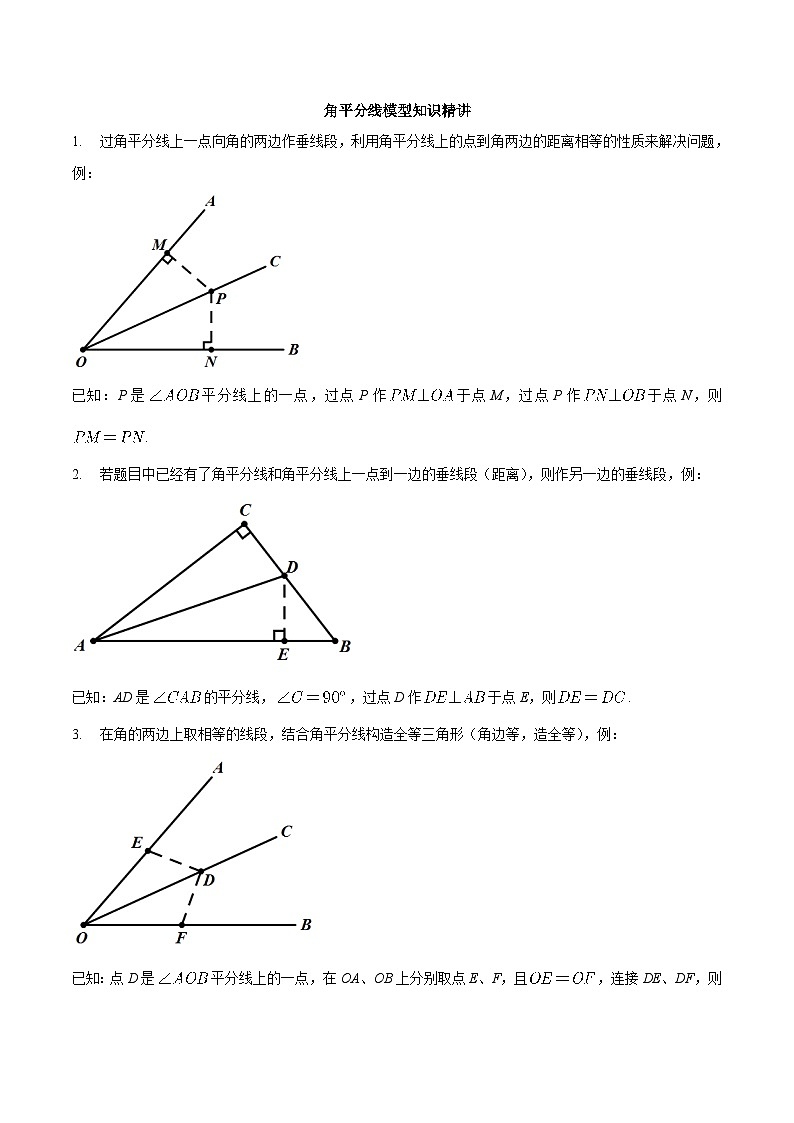
已知：P是平分线上的一点，过点P作于点M，过点P作于点N，则.
2.若题目中已经有了角平分线和角平分线上一点到一边的垂线段（距离），则作另一边的垂线段，例：
已知：AD是的平分线，，过点D作于点E，则.
3.在角的两边上取相等的线段，结合角平分线构造全等三角形（角边等，造全等），例：
已知：点D是平分线上的一点，在OA、OB上分别取点E、F，且，连接DE、DF，则.
4.过角平分线上一点作角的一边的平行线，构造等腰三角形，例：
已知：点D是平分线上的一点，过点D作，则是等腰三角形，即.
证明：是的平分线，，
又，是等腰三角形.
5.有角平分线时，过角一边上的点作角平分线的平行线，交角的另一边所在直线于一点，也可构造等腰三角形，例：
已知：OC平分，点D是OA上一点，过点D作交OB的反向延长线于点E，则.
6.从角的一边上的一点作角平分线的垂线，使之与角的另一边相交，则可得到一个等腰三角形，例：
已知：OE平分∠AOB，点D在OA上，DE⊥OE，则可延长DE交OB于点F，则DE＝EF，OD＝OF，∠ODF＝∠OFD.
7.有角平分线时，可将等角放到直角三角形中，构造相似三角形，也可以另加一对相等的角构造相似三角形，例：
（1）已知：OC平分，点E、F分别在OA、OB上，过点E作于点M，过点F作于点N，则，如图所示：
（2）已知：OC平分，点E、F在OC上，作于点M，作于点N，则，如图所示：
（3）已知：OC平分，点E、F在OC上，作，则，如图所示：
8.利用“在同圆或等圆中，相等的圆周角（圆心角）所对的弦相等”可得相等线段，例：
已知：∠BAC是圆O的圆周角，∠DOE是圆O的圆心角，AF平分∠BAC，OG平分∠DOE，连接BF、CF、DG、EG，则BF＝CF，DG＝EG.
9.【内内模型】如图，两个内角平分线交于点D，则.
证明：平分，平分，，
在中， ①
在中， ②
，
由得，
即.
10.【内外模型】如图，的一个内角平分线和一个外角平分线交于点D，则.
证明：平分，平分，，
在中，，即 ①
在中， ②
由得
，即.
11.【外外模型】如图，两个外角的角平分线交于点D，则.
证明：平分，平分，，
在中，，即 ①
，
②
由①＝②，得，
在中，，
，，
即，
由④可得，代入③式可得，
整理可得.