中考数学二轮复习几何专项知识精讲+基础提优训练专题06 半角模型巩固练习（提优）（2份，原卷版+解析版）

这是一份中考数学二轮复习几何专项知识精讲+基础提优训练专题06 半角模型巩固练习（提优）（2份，原卷版+解析版），文件包含中考数学二轮复习几何专项知识精讲+基础提优训练专题06半角模型巩固练习提优-原卷版doc、中考数学二轮复习几何专项知识精讲+基础提优训练专题06半角模型巩固练习提优-解析版doc等2份试卷配套教学资源，其中试卷共15页， 欢迎下载使用。
【解答】见解析
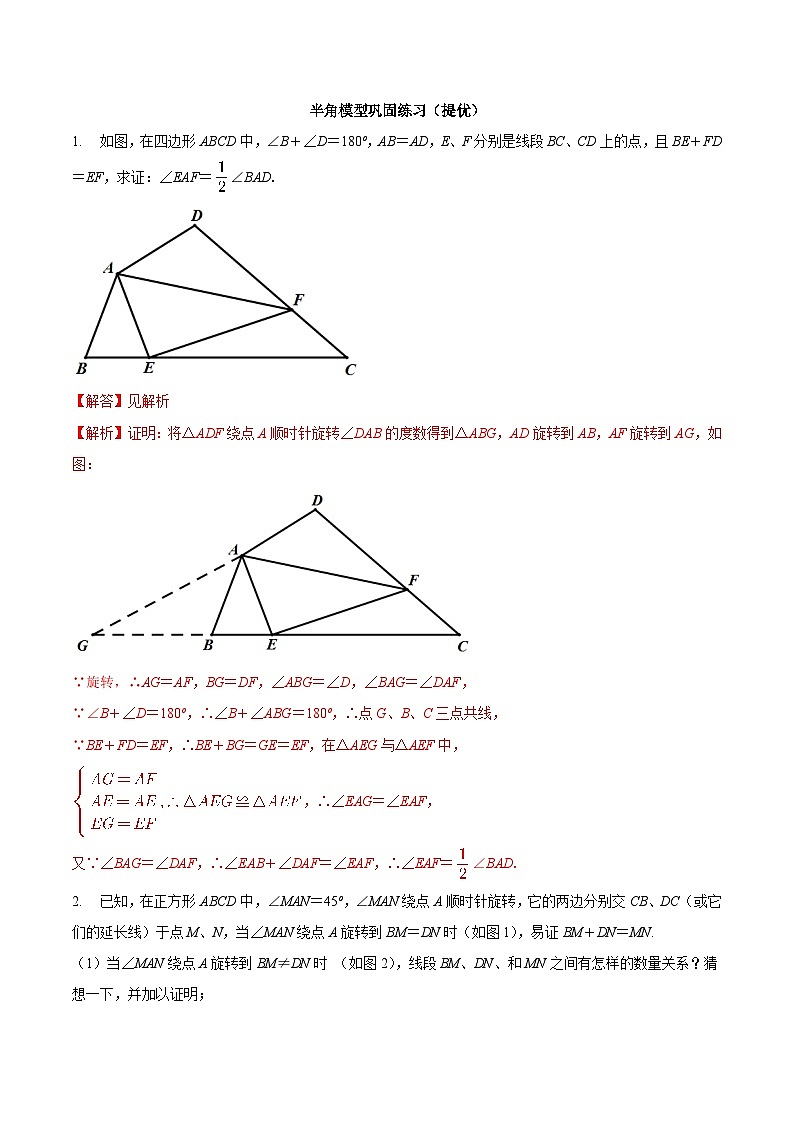
【解析】证明：将△ADF绕点A顺时针旋转∠DAB的度数得到△ABG，AD旋转到AB，AF旋转到AG，如图：
∵旋转，∴AG＝AF，BG＝DF，∠ABG＝∠D，∠BAG＝∠DAF，
∵∠B＋∠D＝180º，∴∠B＋∠ABG＝180º，∴点G、B、C三点共线，
∵BE＋FD＝EF，∴BE＋BG＝GE＝EF，在△AEG与△AEF中，
，∴∠EAG＝∠EAF，
又∵∠BAG＝∠DAF，∴∠EAB＋∠DAF＝∠EAF，∴∠EAF＝∠BAD.
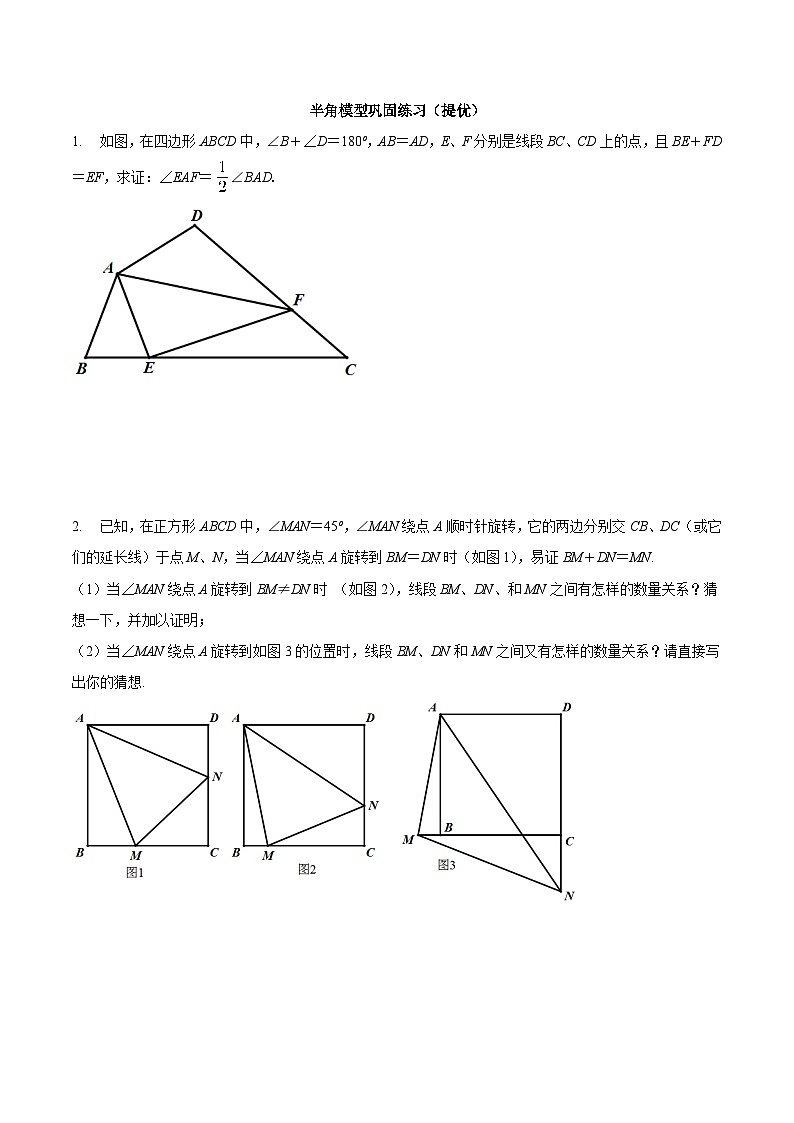
2.已知，在正方形ABCD中，∠MAN＝45º，∠MAN绕点A顺时针旋转，它的两边分别交CB、DC（或它们的延长线）于点M、N，当∠MAN绕点A旋转到BM＝DN时（如图1），易证BM＋DN＝MN.
（1）当∠MAN绕点A旋转到BM≠DN时 （如图2），线段BM、DN、和MN之间有怎样的数量关系？猜想一下，并加以证明；
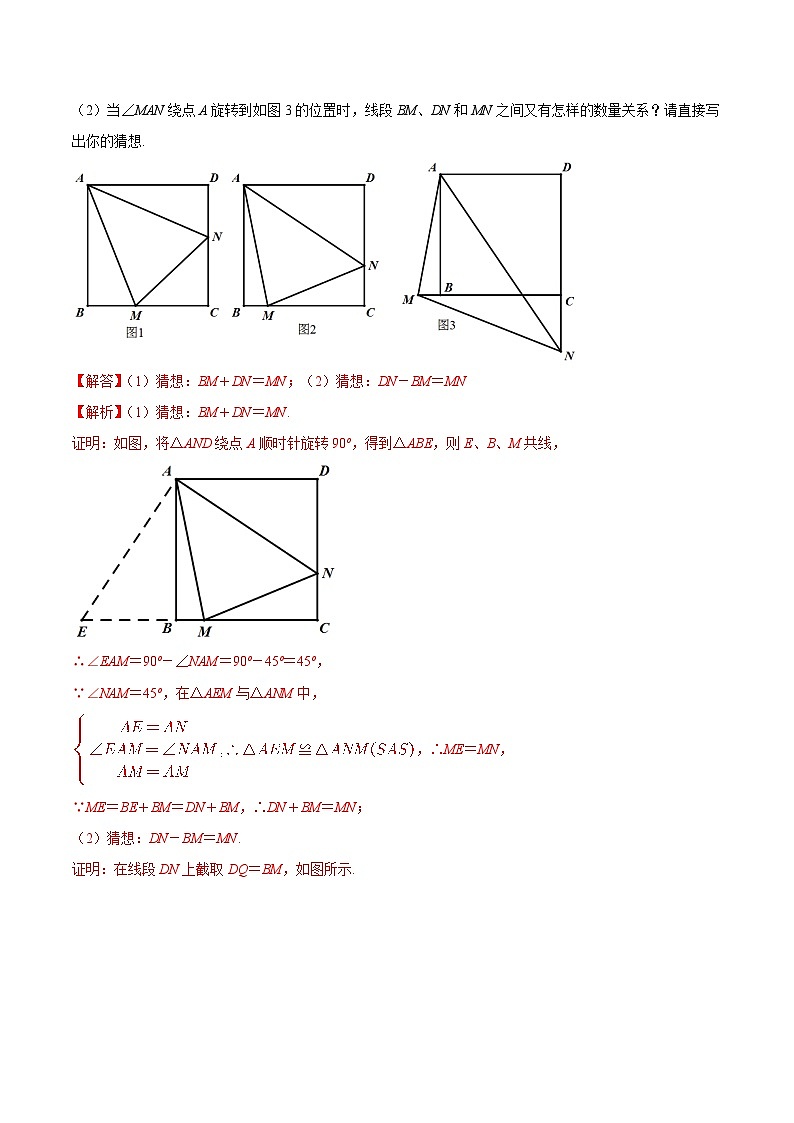
（2）当∠MAN绕点A旋转到如图3的位置时，线段BM、DN和MN之间又有怎样的数量关系？请直接写出你的猜想.
【解答】（1）猜想：BM＋DN＝MN；（2）猜想：DN－BM＝MN
【解析】（1）猜想：BM＋DN＝MN.
证明：如图，将△AND绕点A顺时针旋转90º，得到△ABE，则E、B、M共线，
∴∠EAM＝90º－∠NAM＝90º－45º＝45º，
∵∠NAM＝45º，在△AEM与△ANM中，
，∴ME＝MN，
∵ME＝BE＋BM＝DN＋BM，∴DN＋BM＝MN；
（2）猜想：DN－BM＝MN.
证明：在线段DN上截取DQ＝BM，如图所示.
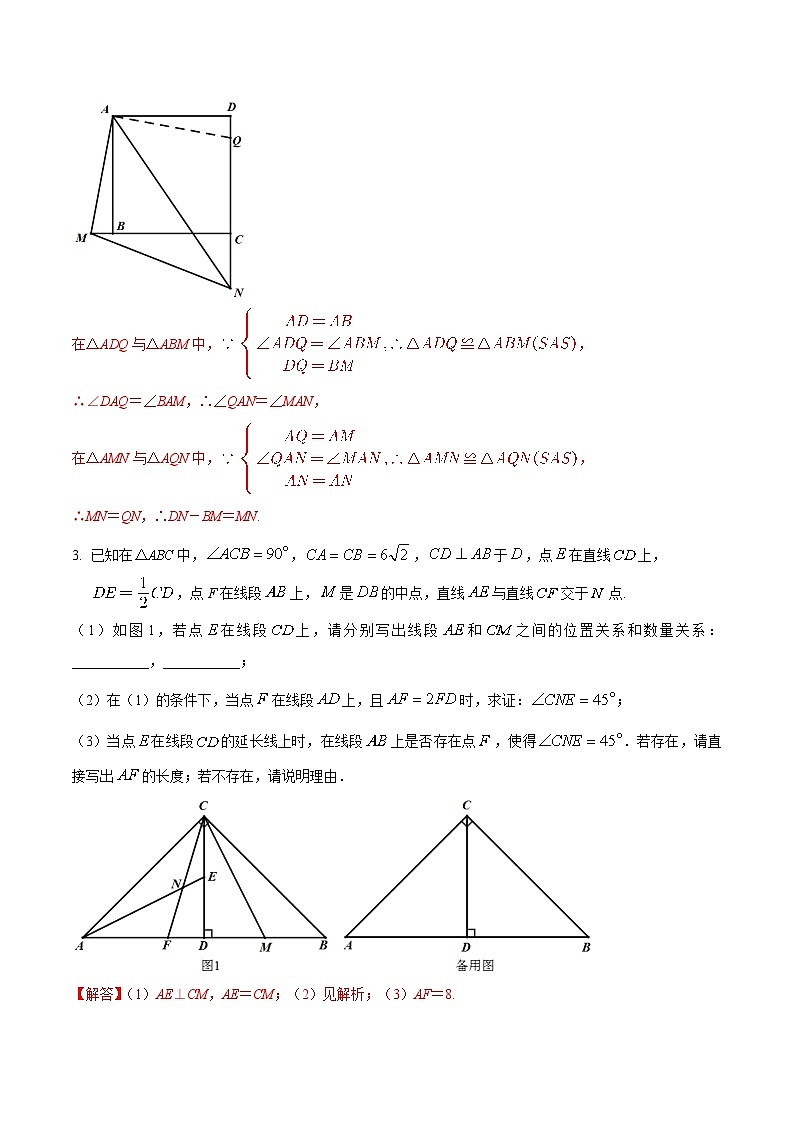
在△ADQ与△ABM中，，
∴∠DAQ＝∠BAM，∴∠QAN＝∠MAN，
在△AMN与△AQN中，，
∴MN＝QN，∴DN－BM＝MN.
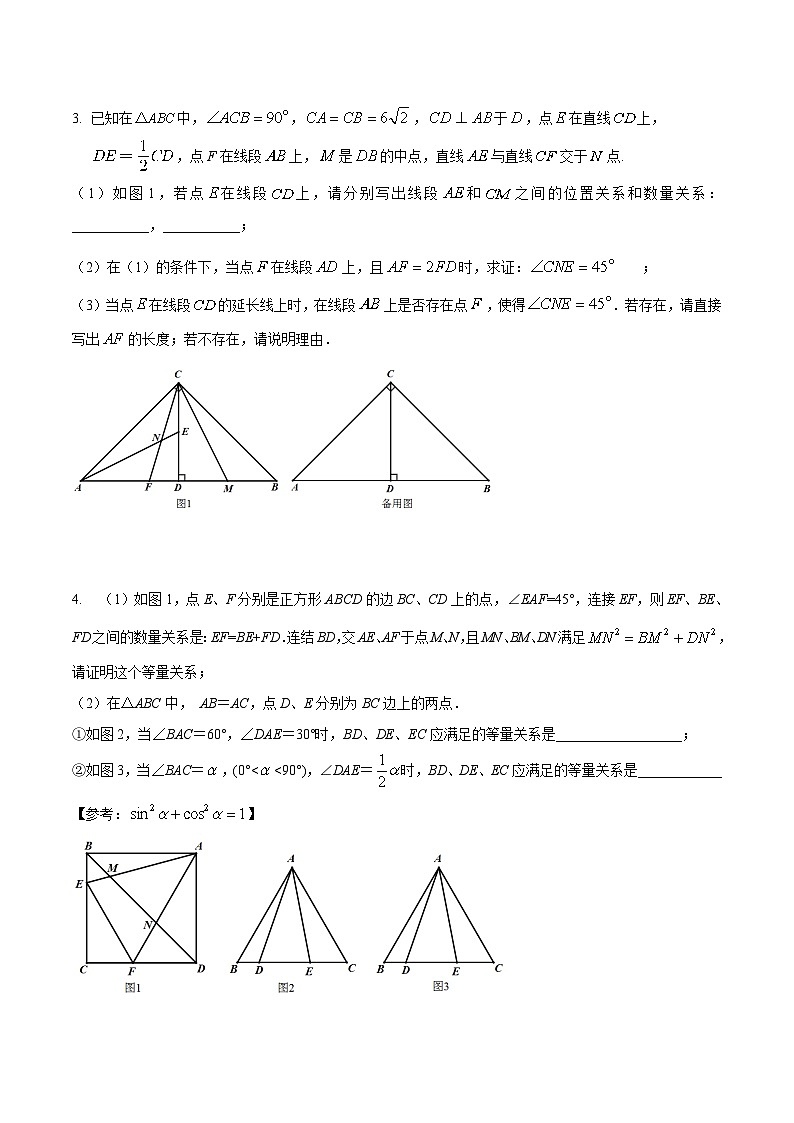
3.已知在中，，，于，点在直线上，，点F在线段上，是的中点，直线与直线交于点.
（1）如图1，若点在线段上，请分别写出线段和之间的位置关系和数量关系：___________，___________；
（2）在（1）的条件下，当点在线段上，且时，求证：；
（3）当点在线段的延长线上时，在线段上是否存在点，使得．若存在，请直接写出的长度；若不存在，请说明理由．
【解答】（1）AE⊥CM，AE＝CM；（2）见解析；（3）AF＝8.
【解析】（1）AE⊥CM，AE＝CM.
如图，延长AE交CM于点H.
∵∠ACB＝90º，CA＝CB＝，CD⊥AB于点D，
∴∠CAB＝∠CBA＝∠ACD＝∠BCD＝45º，AD＝BD＝CD＝AB，
∵M是DB的中点，∴，
∵.
在△AEC与△CMB中，，
∴AE＝CM，∠CAE＝∠BCM，
∵∠ACM＋∠BCM＝90º，∴∠ACM＋∠CAE＝90º，∴∠ACH＝90º，
∴AH⊥CM，∴AE⊥CM，AE＝CM；
（2）如图，过点A作AG⊥AB,且AG=BM,，连接CG、FG,延长AE交CM于H.
∵∠CAB＝90º， CA＝CB＝，
∴∠CAB=∠CBA=45°，，∴∠GAC=∠MBC=45°，
∵CD⊥AB，∴CD=AD=BD= ，
∵ M是DB的中点,∴BM＝DM＝3，∴AG＝3，
∵AF＝2FD，∴AF＝4，DF＝2，∴FM＝FD＋DM＝2＋3＝5，
∵AG⊥AF，，∴FG＝FM，
在△CAG和△CBM中，，
∴CG＝CM，∠ACG＝∠BCM，
∴∠MCG＝∠ACM＝∠ACG＝∠ACM＋∠BCM＝90º，在△FCG和△FCM中，
，∴∠FCG＝∠FCM，∴∠FCH＝45º，
由（1）知AE⊥CM，∴∠CHN＝90º，∴∠CNE＝45º；
（3）存在，如图作BH⊥CN.
由条件可得∠CHB=90º，
∵CD⊥AB，∴∠ADE=90º，∠CHB=∠ADE，
∵∠ACB=90∴∠CAB=∠CBA=45°，∴∠GAC=∠MBC=45º，
∵CD⊥AB，，DE=3.
在Rt△ADE中，由勾股定理可得，
∵∠CNE＝45º，∴∠CBA＝∠CNE，
∵∠AFN＝∠CFB，∴∠NAF＝∠BCF，∴△ADE∽△CHB，
，，
设 ,则，在Rt△CDF中,由勾股定理,得，
∵∠CDF＝∠BHF＝90º，∠DFC＝∠HFB，∴△CDF∽△BHF，
，解得（舍），∴AF＝6＋2＝8.
4.（1）如图1，点E、F分别是正方形ABCD的边BC、CD上的点，∠EAF=45°，连接EF，则EF、BE、FD之间的数量关系是：EF=BE+FD．连结BD，交AE、AF于点M、N，且MN、BM、DN满足，请证明这个等量关系；
（2）在△ABC中， AB＝AC，点D、E分别为BC边上的两点．
①如图2，当∠BAC＝60°，∠DAE＝30°时，BD、DE、EC应满足的等量关系是__________________；
②如图3，当∠BAC＝，(0°