中考数学二轮复习几何专项知识精讲+基础提优训练专题24 正方形存在性问题巩固练习（基础）（2份，原卷版+解析版）

这是一份中考数学二轮复习几何专项知识精讲+基础提优训练专题24 正方形存在性问题巩固练习（基础）（2份，原卷版+解析版），文件包含中考数学二轮复习几何专项知识精讲+基础提优训练专题24正方形存在性问题巩固练习基础原卷版doc、中考数学二轮复习几何专项知识精讲+基础提优训练专题24正方形存在性问题巩固练习基础解析版doc等2份试卷配套教学资源，其中试卷共36页， 欢迎下载使用。
（1）求抛物线的解析式；
（2）点Q在平面内，在第一象限内是否存在点P，使以A，B，P，Q为顶点的四边形是正方形？若存在，直接写出点P的坐标；若不存在，请说明理由．
【分析】（1）把已知点的坐标代入抛物线解析式即可求得a、b的值，可求得抛物线解析式；
（2）可先求得A、B两点的坐标，可求得AB长度，分别过A、B两点作AB的垂线，则点P可以在这两条直线上，且PA＝AB或PB＝AB，分别求得两垂线的解析式，设出点P的坐标，再根据线段相等可列出方程，可求得点P的坐标．
【解答】解：
（1）∵抛物线y＝﹣ax2+bx+5过点（1，2）、（4，5），
∴，解得，
∴抛物线解析式为y＝x2﹣4x+5；
（2）在y＝x2﹣4x+5中，令x＝0可得y＝5，
∴B（0，5），
∵y＝x2﹣4x+5＝（x﹣2）2+1，
∴A（2，1），
∴AB2，
设直线AB解析式为y＝kx+n，则有，解得，
∴直线AB解析式为y＝﹣2x+5，
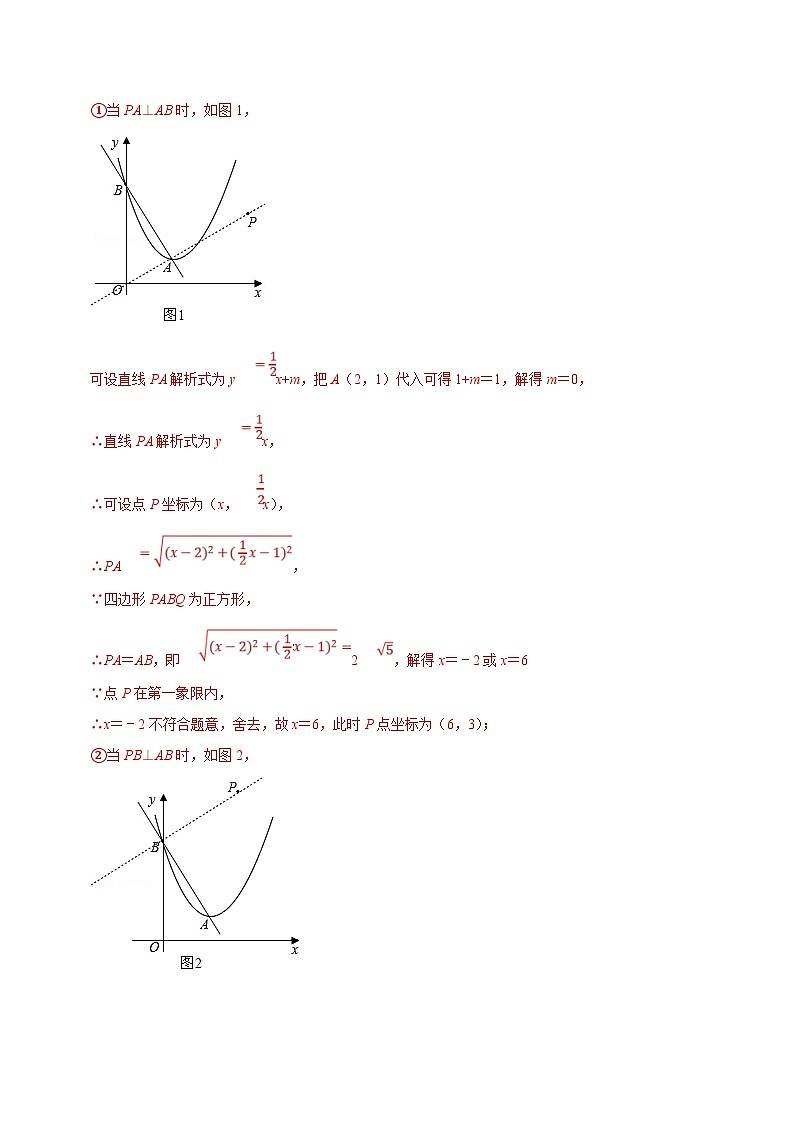
①当PA⊥AB时，如图1，
可设直线PA解析式为yx+m，把A（2，1）代入可得1+m＝1，解得m＝0，
∴直线PA解析式为yx，
∴可设点P坐标为（x，x），
∴PA，
∵四边形PABQ为正方形，
∴PA＝AB，即2，解得x＝﹣2或x＝6
∵点P在第一象限内，
∴x＝﹣2不符合题意，舍去，故x＝6，此时P点坐标为（6，3）；
②当PB⊥AB时，如图2，
可设直线PB解析式为yx+s，把B（0，5）代入可得s＝5，
∴直线PB解析式为yx+5，
∴可设P点坐标为（x，x+5），
∴PB，
同理可得2，解得x＝﹣4（舍去）或x＝4，此时P点坐标为（4，7），
当AB是正方形的对角线时，因为等P在第一象限，可得P（3，4），
综上可知存在满足条件的点P，其坐标为（6，3）或（4，7）或（3，4）．
【点评】本题为二次函数的综合应用，涉及待定系数法、二次函数的性质、勾股定理、正方形的性质、方程思想及分类讨论思想等知识点．在（1）中注意待定系数法的应用步骤，在（2）中确定出P点的位置是解题的关键，注意利用正方形的性质列方程．本题考查知识点较多，综合性较强，但难度不大．
2．如图，在矩形ABCD中，AB＝16cm，AD＝6cm，动点P，Q分别从点A，C同时出发，点P以每秒3cm的速度向点B移动，点Q以每秒2cm测得速度向点D移动，当点P到达点B处时，两点均停止移动
（1）P，Q两点出发多长时间，线段PQ的长度为10cm？
（2）是否存在某一时刻，使四边形PBCQ为正方形？若存在，求出该时刻；若不存在，请说明理由．
【分析】（1）过点P作PH⊥CD，利用勾股定理解答即可；
（2）利用正方形的性质进行解答即可．
【解答】解：（1）过点P作PH⊥CD于点H，
∴HQ＝16﹣5t，
∴PQ2＝PH2+HQ2，
即102＝（16﹣5t）2+62，
解得：，
答：P，Q两点出发或秒，线段PQ的长度为10cm；
（2）∵四边形PBCQ是正方形，
∴BP＝CQ，即16﹣3t＝2t，
解得：t，
∵，
∴不成立．
【点评】此题考查正方形的性质，关键是根据利用正方形的性质进行解答．
3．如图，在▱ABCD中，AB＝4，BC＝8，∠B＝60°，点P以每秒2个单位速度，从点B出发沿射线BA方向运动，同时直线l以每秒1个单位速度，从CD出发沿射线CB方向运动，分别交BC，AC于点G，H，连结PG，设运动的时间为t，当G与B重合时，运动停止．
（1）当t为何值时，以P，G，H，A为顶点的四边形是平行四边形；
（2）在运动过程中，是否存在以P，G，H，A为顶点的四边形是正方形？若存在，请求出t的值；若不存在，请说明理由．
【分析】（1）当PA＝GH时，以P，G，H，A为顶点的四边形是平行四边形，列出方程即可解决．
（2）不存在，根据（1）中的两种情形进行证明．
【解答】解：（1）当PA＝GH时，以P，G，H，A为顶点的四边形是平行四边形，
如图取BC中点M，连接AM，
∵AB＝4，BM＝MC＝4，∠ABC＝60°，
∴△ABM是等边三角形，
∴AM＝MC＝4，∠AMB＝60°，
∴∠MAC＝∠MCA，
∵∠AMB＝∠MAC+∠MCA，
∴∠BCA＝30°，
∴∠BAC＝90°，
∵AB∥GH，
∴∠GHC＝∠BAC＝90°
∵PA＝4﹣2t或2t﹣4，GHCGt
由题意：4﹣2tt或2t﹣4，
t或，
（2）不存在．理由如下：
由（1）可知①t时 四边形APGH是平行四边形，
∵∠PAH＝90°，
∴四边形APGH是矩形，
∵GH，PG，
∴GH≠PG，
∴四边形APGH不是正方形．
②t时，点P在BA的延长线上，四边形PAGH显然不是正方形．
【点评】本题考查平行四边形的判定和性质、正方形的判定和性质，解决问题的关键是用方程的思想思考问题，属于中考常考题型．
4．如图，在平面直角坐标系中，点A、点B分别在y轴、x轴的正半轴上，且满足（OB﹣40）2＝0，若点P从A点出发，以每秒2个单位长度的速度沿线段AO运动，同时点Q从B点出发，以每秒5个单位长度的速度沿线段BA运动，连接PQ，点P，Q的运动时间为t秒．
（1）求直线AB的解析式；
（2）设△APQ的面积为S，当t为何值时，S＝64？
（3）点N在x轴上，在坐标平面上是否存在点M，使以点M，P，Q，N为顶点的四边形在某一时刻为正方形？若存在，请直接写出点M的坐标；若不存在，请说明理由．
【分析】（1）先求出方程的根，得出A、B两点的坐标，然后根据待定系数法求得即可；
（2）根据题意得出AP＝2t，AQ＝50﹣5t，作QM⊥OA于M，根据三角形相似等边成比例求得QM（50﹣t），根据三角形面积公式即可求得△APQ的面积S与t的函数关系，把S＝64代入即可求得t的值；
（3）分别作QG⊥OB，QH⊥OA，MK⊥y轴，ML⊥x轴，根据题意得四边形OGQH是正方形，NG＝PH＝MK＝ML，根据三角函数得出，，即可求得QG＝3t，BG＝4t，得出3t＝40﹣4t，求得t，求得AP，OP的值，即可求得PH的值，从而求得NG＝PH＝MK＝ML，即可得出M点的坐标．
【解答】解：（1）（OB﹣40）2＝0，
∴OA＝30，OB＝40，
∴A（0，30），B（40，0），
设直线AB的解析式为y＝kx+b，
∴，解得
∴直线AB的解析式为yx+30；
（2）由题意得，AP＝2t，AQ＝50﹣5t
作QM⊥OA于M，如图1，
∴△ANQ∽△AOB，
∴，即，
∴QM（50﹣5t），
∴SAP•QM2t•（50﹣5t）＝﹣4t2+40t；
把S＝64代入得，64＝﹣4t2+40t，解得t＝2或8，
∵0≤t≤15，
故当t＝2或8时，S＝64；
（3）如图2，分别作QG⊥OB，QH⊥OA，MK⊥y轴，ML⊥x轴，
由四边形PQNM是正方形，则四边形OGQH是正方形，
NG＝PH＝MK＝ML，
∵QG⊥OB，
∴，
∵QB＝5t，
∴QG＝3t，BG＝4t，
∴OG＝40﹣4t，
∴3t＝40﹣4t，
∴t，
∴AP＝2t，QG，
∴OH，
∴PH＝30，
∴NG＝PH＝MK＝ML，
∴M（，）．
【点评】本题是一次函数的综合题，考查了待定系数法求一次函数的解析式，三角形相似的判定和性质，直角三角函数的应用，正方形的性质，三角形全等的性质等，作出辅助线构建直角三角形是解题的关键．
5．如图，在平面直角坐标系中，O是坐标原点，点A的坐标是（1，3），点P的坐标是（0，b）（b≠0）．直线AP交x轴于点B，记点P关于x轴的对称点为P′，点Q为x轴上一动点．
（1）当b＝1时，求OB的长；
（2）当0＜b＜3时，用含b的代数式表示OB的长；
（3）是否存在四边形PBP′Q，使四边形PBP′Q为正方形？若存在，请求出所有满足条件的b和点Q的坐标；若不存在，请说明理由．
【分析】（1）根据b的值表示出直线AP解析式，把A坐标代入求出k的值，确定出AP解析式，进而得出B坐标，确定出OB的长；
（2）设出AP解析式为y＝kx+b，把A坐标代入表示出k，即可表示出OB的长；
（3）存在四边形PBP′Q，使四边形PBP′Q为正方形，若四边形PBP′Q为正方形，则有OB＝OP＝OP′＝OQ，列出关于b的方程，求出方程的解得到b的值，即可确定出Q坐标．
【解答】解：（1）由b＝1，得到P（0，1），
设直线AP解析式为y＝kx+1，
把A（1，3）代入得：3＝k+1，
解得：k＝2，
∴直线OP解析式为y＝2x+1，
令y＝0，得到x，
∴B（，0），即OB；
（2）根据题意得：直线AP解析式为y＝kx+b，
把（1，3）代入得：3＝k+b，即k＝3﹣b，
∴直线解析式为y＝（3﹣b）x+b，
令y＝0，得到x，即OB；
（3）存在四边形PBP′Q，使四边形PBP′Q为正方形，理由为：
若四边形PBP′Q为正方形，则有OB＝OP＝OP′＝OQ，即b，
解得：b＝2，
则b＝2，Q（2，0）．
【点评】此题属于一次函数综合题，涉及的知识有：待定系数法确定一次函数解析式，坐标与图形性质，正方形的性质，以及一次函数的性质，熟练掌握待定系数法是解本题的关键．
6．如图，在平面直角坐标系中，四边形OABC为矩形，点A、点C分别在y轴、x轴的正半轴上，OA，OC的长分别是方程x2﹣7x+12＝0的两根（OA＜OC）．P为直线AB上一动点，直线PQ⊥OP交直线BC于点Q．
（1）求点B的坐标；
（2）当点P在线段AB上运动（不与A，B重合）时，设点P的横坐标为m，线段CQ的长度为l．求出l关于m的函数解析式；
（3）在坐标平面内是否存在点D，使以O、P、Q、D为顶点的四边形为正方形？若存在，请直接写出D点的坐标；若不存在，请说明理由．
【分析】（1）通过解方程求出线段的长度，利用矩形的性质得到AB＝4，BC＝3，求得B（4，3）；
（2）因为点P在线段AB上，点P的横坐标为m，用m表示出AP的长度，利用相似三角形的性质列出比例式求出l关于m的函数解析式；
（3）如图，过点D作DE⊥OC于E，由以O、P、Q、D为顶点的四边形为正方形，得到OP＝PQ＝OD，通过三角形全等，对应边相等求得AP＝m＝1，再根据另一对三角形全等得到点D的坐标．
【解答】解：（1）解方程x2﹣7x+12＝0得：x1＝3，x2＝4，
∴OA＝3，OC＝4，
∴A（0，3），C（4，0），
∵四边形OABC为矩形，
∴AB＝4，BC＝3，
∴B（4，3）；
（2）点P在线段AB上，点P的横坐标为m，
∴AP＝m，
∵CQ＝l，
∴BQ＝3﹣l，
∵∠OAP＝∠B＝∠OPQ＝90°，
∴∠APO+∠BPQ＝∠APO+∠AOP＝90°，
∴∠APO＝∠BPQ，
∴△APO∽△BPQ，
∴，
即，
∴lm2m+3；
（3）存在，
如图，过点D作DE⊥OC于E，
∵四边形ODQP是正方形，
∴OP＝PQ＝OD，
在△AOP与△BPQ中，
，
∴△AOP≌△BPQ（AAS），
∴PB＝OA＝3，
∴AP＝BP＝1，
在△AOP与△OED中，
，
∴△AOP≌△OEP（AAS），
∴OE＝AO＝3，DE＝AP＝1，
∴D（3，﹣1）．
若点P在点B的右边，同理可得D（﹣3，7）
综上所述D（3，﹣1）或（﹣3，7）
【点评】本题考查了在平面直角坐标系中求点的坐标，相似三角形的判定和性质，全等三角形的判定与性质，特别是（3）正确的画出图形是解题的关键．
7．在平面直角坐标系中，直线AB的解析式为y＝﹣2x+12，点C是线段AB的中点．
（1）如图，求直线OC的解析式；
（2）点D从点O出发，沿射线OC方向运动，速度为每秒个单位，过点D作x轴的垂线，交直线AB于点E，设△EDC的面积为S，点D的运动时间为t，写出S与t的函数关系式，并写出自变量t的取值范围；
（3）在（2）的条件下，当点D运动时间恰好为2秒时，点P为直线AD上的动点，在平面内，是否存在点Q，使以点O，A，P，Q为顶点的四边形为正方形？若存在，请求出Q点的坐标；若不存在，请说明理由．
【分析】（1）先由直线AB的解析式为y＝﹣2x+12，求出A（6，0），B（0，12），再根据中点坐标公式得到线段AB的中点C的坐标为（3，6）．然后利用待定系数法即可求出直线OC的解析式；
（2）先求出点D运动到点C所需时间为：33秒，设ED⊥x轴于点M．根据直角三角形的性质得出OC＝AC，那么∠DOM＝∠OAB．解直角△DOM，求出OM＝OD•cs∠DOM＝t，DM＝OD•sin∠DOM＝2t，即D（t，2t），E（t，﹣2t+12）．再分两种情况进行讨论：①0＜t＜3；②t＞3．根据三角形的面积公式求解即可；
（3）当点D运动时间为2秒时，OD＝2，D（2，4）．利用待定系数法求出直线AD的解析式为y＝﹣x+6．再分两种情况进行讨论：①OA为正方形的边，根据正方形的性质求出Q1点的坐标为（6，6）；②OA为正方形的对角线，易求Q2点的坐标为（3，﹣3）．
【解答】解：（1）∵直线AB的解析式为y＝﹣2x+12，
∴当y＝0时，﹣2x+12＝0，解得x＝6，即A（6，0），
当x＝0时，y＝12，即B（0，12），
∵点C是线段AB的中点，
∴点C坐标为（3，6）．
设直线OC的解析式为y＝kx，
则3k＝6，解得k＝2，
故直线OC的解析式为y＝2x；
（2）∵OC3，点D从点O出发，沿射线OC方向运动，速度为每秒个单位，
∴点D运动到点C所需时间为：33（秒）．
设ED⊥x轴于点M．
∵OC为直角△ABC斜边AB的中线，
∴OC＝AC，
∴∠DOM＝∠OAB．
∵在直角△DOM中，ODt，
∴OM＝OD•cs∠DOM＝OD•cs∠OABt•t，
DM＝OD•sin∠DOM＝OD•sin∠OABt•2t，
∴D（t，2t），
∴E（t，﹣2t+12）．
如图，分两种情况：
①当0＜t＜3时，D在线段OC上，
∵DE＝﹣2t+12﹣2t＝﹣4t+12，C到DE的距离为：3﹣t，
∴S△CDE（﹣4t+12）（3﹣t）＝2t2﹣12t+18，
即S＝2t2﹣12t+18；
②当t＞3时，D线段OC的延长线上，
∵DE＝2t﹣（﹣2t+12）＝4t﹣12，C到DE的距离为：t﹣3，
∴S△CDE（4t﹣12）（t﹣3）＝2t2﹣12t+18，
即S＝2t2﹣12t+18；
综上所述，S与t的函数关系式为S＝2t2﹣12t+18（t＞0且t≠3）；
（3）当点D运动时间为2秒时，OD＝2，D（2，4）．
设直线AD的解析式为y＝mx+n，
∵A（6，0），D（2，4），
∴，解得，
∴直线AD的解析式为y＝﹣x+6，
∴直线AD与y轴交点为（0，6）．
以点O，A，P，Q为顶点的四边形为正方形时，分两种情况：
①如果OA为正方形的边，如图，作正方形OP1Q1A，则P1为直线AD与y轴交点，
∵OA＝OP1＝6，∠OAQ1＝90°，
∴Q1点的坐标为（6，6）；
②如果OA为正方形的对角线，设OA中点为N，则N（3，0），
当x＝3时，y＝﹣3+6＝3．
作OA的垂直平分线l，交直线AD于点P2，
则P2点的坐标为（3，3），在l上截取NQ2＝NP2，
则四边形OP2AQ2是正方形，此时Q2点的坐标为（3，﹣3）．
综上所述，所求Q点的坐标为Q1（6，6），Q2（3，﹣3）．
【点评】本题是一次函数综合题，涉及到利用待定系数法求直线的解析式，一次函数图象上点的坐标特征，中点坐标公式，三角形的面积，勾股定理，直角三角形的性质，正方形的判定与性质，综合性较强，难度适中．利用数形结合、分类讨论及方程思想是解题的关键．
8．如图，平面直角坐标系中，直线AB分别交x轴正半轴于点A，交y轴正半轴于点B，且OA、OB（OA＜OB）的长是方程x2﹣12x+32＝0的两个根．
（1）求sin∠ABO的值；
（2）已知点C是OB的中点，当点P在射线BA上运动到S△AOC＝S△AOP时，求经过点P的反比例函数解析式；
（3）若点Q在线段AB上，平移直线OQ交x轴于点D，交y轴于点E．当M（a，4）时，是否存在点N使得以点D、E、M、N为顶点的四边形是正方形？若存在直接写出点N的坐标；若不存在请说明理由．
【分析】（1）可求得方程的两根分别为4和8，且OA＜OB，所以求得OA＝4，OB＝8，再根据勾股定理，求得AB的长，即可解答；
（2）先求出直线AB的解析式，再根据S△AOC＝S△AOP时，求出点P的纵坐标，把点P的纵坐标代入直线AB的解析式求点P的横坐标，即可解答；
（3）画出图形，根据正方形的性质，即可解答．
【解答】解：（1）x2﹣12x+32＝0
解得：x1＝4，x2＝8，
∵OA＜OB，
∴OA＝4，OB＝8，
∴AB，
∴sin∠ABO．
（2）如图，连接AC，OP，过点P作PD⊥OA于点D，
设直线AB的解析式为：y＝kx+b，
把A（4，0），B（0，8）代入y＝kx+b得：
，
解得：，
∴直线AB的解析式为：y＝﹣2x+8，
∵OB＝8，点C是OB的中点，
∴OC＝4，
当点P在射线BA上运动到S△AOC＝S△AOP时，
∴
即，
∴PD＝4，
∴设P（x，4），
把P（x，4）代入y＝﹣2x+8得：﹣2x+8＝4，
解得：x＝2，
∴P（2，4），
设经过点P的函数解析式为：，
∴，
∴k＝8，
∴经过点P的函数解析式为：．
（3）存在；如图，
①当直线OQ向下平移时，DENM为正方形，
当点M在y轴上时，此时点M的坐标为（0，4），此时点M与点E关于x轴对称，点D与点N关y轴对称，
根据正方形的性质，OM＝OE＝OD＝ON＝4，
所以N（﹣4，0）；
②当直线OQ向上平移时，平移到与y轴的交点为（0，4），与x轴交点为（﹣4，0），DENM为正方形，
∴O（D）＝4，O（E）＝4，
∴根据中点的性质，此时N的坐标为（﹣4，8）
∴N（﹣4，0）或N（﹣4，8）．
【点评】本题是一次函数的综合题型，其中涉及到的知识点有运用待定系数法求一次函数的解析式，正方形的性质，综合性较强，难度适中．运用数形结合、分类讨论是解题的关键．
9．如图，抛物线yx2x﹣2，经过点C（﹣3，h），CD⊥x轴，垂足为D点，Rt△AOB≌Rt△CDA，A、B分别在x轴，y轴上，在对称轴右侧的抛物线上是否存在两点P、Q，使四边形ABPQ是正方形？若存在，求出点P、Q的坐标；若不存在，请说明理由．
【分析】将点C（﹣3，h）代入抛物线yx2x﹣2，可求点C的坐标，根据全等三角形的性质可得OA＝CD＝1，OB＝AD＝3﹣1＝2，以AB为边在抛物线的右侧作正方形AQPB，过P作PE⊥y轴，过Q作QG垂直x轴于G，不难得出三角形ABO和三角形BPE和三角形QAG都全等，据此可求出P，Q的坐标，然后将两点坐标代入抛物线的解析式中即可判断出P、Q是否在抛物线上．
【解答】解：在抛物线（对称轴的右侧）上存在点P、Q，使四边形ABPQ是正方形．
把点C（﹣3，h）代入抛物线yx2x﹣2，
则h（﹣3）2（﹣3）﹣2＝1，
则C点坐标为（﹣3，1），
∵Rt△AOB≌Rt△CDA，
∴OA＝CD＝1，
∴OB＝AD＝3﹣1＝2，
以AB为边在AB的右侧作正方形ABPQ，过P作PE⊥OB于E，QG⊥x轴于G，可证△PBE≌△AQG≌△BAO，
∴PE＝AG＝BO＝2，BE＝QG＝AO＝1，
∴P点坐标为（2，1），Q点坐标为（1，﹣1）．
yx2x﹣2，当x＝2时，y＝1；当x＝1时，y＝﹣1．
∴P、Q在抛物线上．
故在抛物线（对称轴的右侧）上存在点P（2，1）、Q（1，﹣1），使四边形ABPQ是正方形．
【点评】本题主要考查了二次函数解析式的应用、正方形的判定、全等三角形的判定和性质等知识点．综合性强，涉及的知识点多，难度较大．
10．如图，已知直线AB与x轴交于点A，与y轴交于点B，线段OA的长是方程x2﹣7x﹣18＝0的一个根，OBOA．请解答下列问题：
（1）求点A，B的坐标；
（2）直线EF交x轴负半轴于点E，交y轴正半轴于点F，交直线AB于点C．若C是EF的中点，OE＝6，反比例函数y图象的一支经过点C，求k的值；
（3）在（2）的条件下，过点C作CD⊥OE，垂足为D，点M在直线AB上，点N在直线CD上．坐标平面内是否存在点P，使以D，M，N，P为顶点的四边形是正方形？若存在，请写出点P的个数，并直接写出其中两个点P的坐标；若不存在，请说明理由．
【分析】（1）解一元二次方程，得到点A的坐标，再根据OBOA可得点B坐标；
（2）利用待定系数法求出直线AB的表达式，根据点C是EF的中点，得到点C横坐标，代入可得点C坐标，根据点C在反比例函数图象上求出k值；
（3）画出图形，可得点P共有5个位置，分别求解即可．
【解答】解：（1）∵线段OA的长是方程x2﹣7x﹣18＝0的一个根，
解得：x＝9或﹣2（舍），而点A在x轴正半轴上，
∴A（9，0），
∵OBOA，
∴B（0，），
（2）∵OE＝6，
∴E（﹣6，0），
设直线AB的表达式为y＝kx+b，将点A和B的坐标代入，
得：，解得：，
∴AB的表达式为：，
∵点C是EF的中点，
∴点C的横坐标为﹣3，代入AB中，y＝6，
则C（﹣3，6），
∵反比例函数经过点C，
则k＝﹣3×6＝﹣18；
（3）存在点P，使以D，M，N，P为顶点的四边形是正方形，
如图，共有5种情况，
在四边形DM1P1N1中，
M1和点A重合，
∴M1（9，0），
此时P1（9，12）；
在四边形DP3M3N3中，可知M在直线y＝x+3上，
联立：，
解得：，
∴M（1，4），
∴P3（1，0），
同理可得：P2（9，﹣12），P4（﹣7，4），P5（﹣15，0）．
故存在点P使以D，M，N，P为顶点的四边形是正方形，
点P的坐标为P1（9，12），P2（9，﹣12），P3（1，0），P4（﹣7，4），P5（﹣15，0）．
【点评】本题考查了解一元二次方程，一次函数表达式，正方形的性质，反比例函数表达式，难度较大，解题的关键是根据图象画出符合条件的正方形．
11．如图，已知直线y＝kx+b与直线yx﹣9平行，且y＝kx+b还过点（2，3），与y轴交于A点．
（1）求A点坐标；
（2）若点P是该直线上的一个动点，过点P分别作PM垂直x轴于点M，PN垂直y轴于点N，在四边形PMON上分别截取：PCMP，MBOM，OEON，NDNP，试证：四边形BCDE是平行四边形；
（3）在（2）的条件下，在直线y＝kx+b上是否存在这样的点P，使四边形BCDE为正方形？若存在，直接写出所有符合的点P的坐标；若不存在，请说明理由．
【分析】（1）直线y＝kx+b与yx﹣9平行，且过点A（2，3），则，即可求解；
（2）证明△OBE≌△PDC（SAS）、△MBC≌△NDE（SAS），即可求解；
（3）证明△DPC≌△CMB（AAS），则CM＝PD，即可求解．
【解答】解：（1）∵直线y＝kx+b与yx﹣9平行，且过点A（2，3），
则，解得，
∴一次函数解析式为yx+4，
当x＝0时，y＝4，
∴A点坐标是（0，4）；
（2）证明：∵PM⊥x轴，PN⊥y轴，
∴∠M＝∠N＝∠O＝90°，
∴四边形PMON是矩形，
∴PM＝ON，OM＝PN，∠M＝∠O＝∠N＝∠P＝90°．
∵PCMP，MBOM，OEON，NDNP，
∴PC＝OE，CM＝NE，ND＝BM，PD＝OB，
在△OBE和△PDC中，OB＝PD，∠O＝∠CPD，OE＝PC，
∴△OBE≌△PDC（SAS），
∴DC＝BE，
同理可证△MBC≌△NDE（SAS），
∴DE＝BC．
∴四边形BCDE是平行四边形；
（3）存在这样的点P，理由：
设点P（m，m+4），
则CMPC|（4m）|＝|m|，PDm，
当四边形BCDE为正方形时，则∠DCB＝90°，DC＝BC，
而∠CBM+∠MCB＝90°，∠MCB+∠DCP＝90°，
∴∠CBM＝∠DCP，
而∠DPC＝∠CMB＝90°，
∴△DPC≌△CMB（AAS），
∴CM＝PD，
即＝|m|m，解得：m或﹣8，
故P点坐标是（，）或（﹣8，8）．
【点评】本题考查的是一函数综合运用，涉及到一次函数的性质、正方形的性质、平行四边形的性质、三角形全等等，有一定的综合性，难度适中．
12．在平面直角坐标系中，直线y＝2x+4与两坐标轴分别交于A，B两点．
（1）若一次函数yx+m与直线AB的交点在第二象限，求m的取值范围；
（2）若M是y轴上一点，N是x轴上一点，直线AB上是否存在两点P，Q，使得以M，N，P，Q四点为顶点的四边形是正方形．若存在，求出M，N两点的坐标，若不存在，请说明理由．
【分析】（1）解析式联立得到2x+4x+m，解得x（m﹣4），根据第二象限的点的横坐标小于0，纵坐标大于0，建立不等式组求解即可；
（2）分三种情况讨论，根据正方形的性质三角形全等的性质，三角形相似的性质即可求得M，N两点的坐标．
【解答】解：（1）联立y＝2x+4与yx+m，得2x+4x+m，解得x（m﹣4），
∵交点在第二象限，
∴，
∴解得﹣1＜m＜4；
（2）当x＝0时，y＝2x+4＝4，
∴A（0，4），
当y＝0时，0＝2x+4，x＝﹣2，
∴B（﹣2，0），
∴OA＝4，OB＝2．
如图1，过点Q作QH⊥x轴于H，
∵MN∥AB，
∴△NMO∽△BAO，
∴，
设ON＝a，则OM＝2a，
∵∠MNQ＝90°，
∴∠QNH+∠MNO＝∠MNO+∠NMO＝90°，
∴∠QNH＝∠NMO，
在△QNH和△NMO中

∴△QNH≌△NMO（AAS），
∴QH＝ON＝a，HN＝OM＝2a，
又∵△BQH∽△BAO，
∴，
∴BHa，
∵OB＝BH+HN+ON，
∴2a+2a+a，解得a，
∴M（0，），N（，0）；
如图2，过点P作PH⊥x轴于H，
易证△PNH∽△BAO，
∴，
设PH＝b，则NH＝2b，
同理证得△PNH≌△NMO，
∴PH＝ON＝b，HN＝OM＝2b，
∴OH＝HN﹣OH＝b，
又∵△BPH∽△BAO，
∴，
∴BHb，
∵OB＝BH+OH，
∴2b+b，解得b，
∴M（0，），N（，0）；
如图3，过点P作PH⊥x轴于H，PE⊥y轴于E，QF⊥y轴于F，易证△PAE∽△BAO，
∴，
设PE＝c，则AE＝2c，
同理证得△PNH≌△PME，
∴PH＝PE＝OE＝c，
∵OA＝AE+OE，
∴4＝2c+c，解得c，
∵△MQF≌△PME，
∴MF＝PE＝OE，EM＝FQ，
∴EM＝OF＝FQ，设EM＝OF＝FQ＝m，则Q（﹣m，﹣m），代入y＝2x+4中，得﹣m＝﹣2m+4，解得m＝4，
∴NO＝NH+OH，
∴N（，0），
∵OF＝m＝4，
∴FM＝PE，
∴OM＝4
∴M（0，）．
综上所述M（0，），N（，0）或M（0，），N（，0）或M（0，），N（，0）；．
【点评】本题考查了两条直线相交或平行问题，一次函数图象和系数的关系，分类讨论是解题的关键．