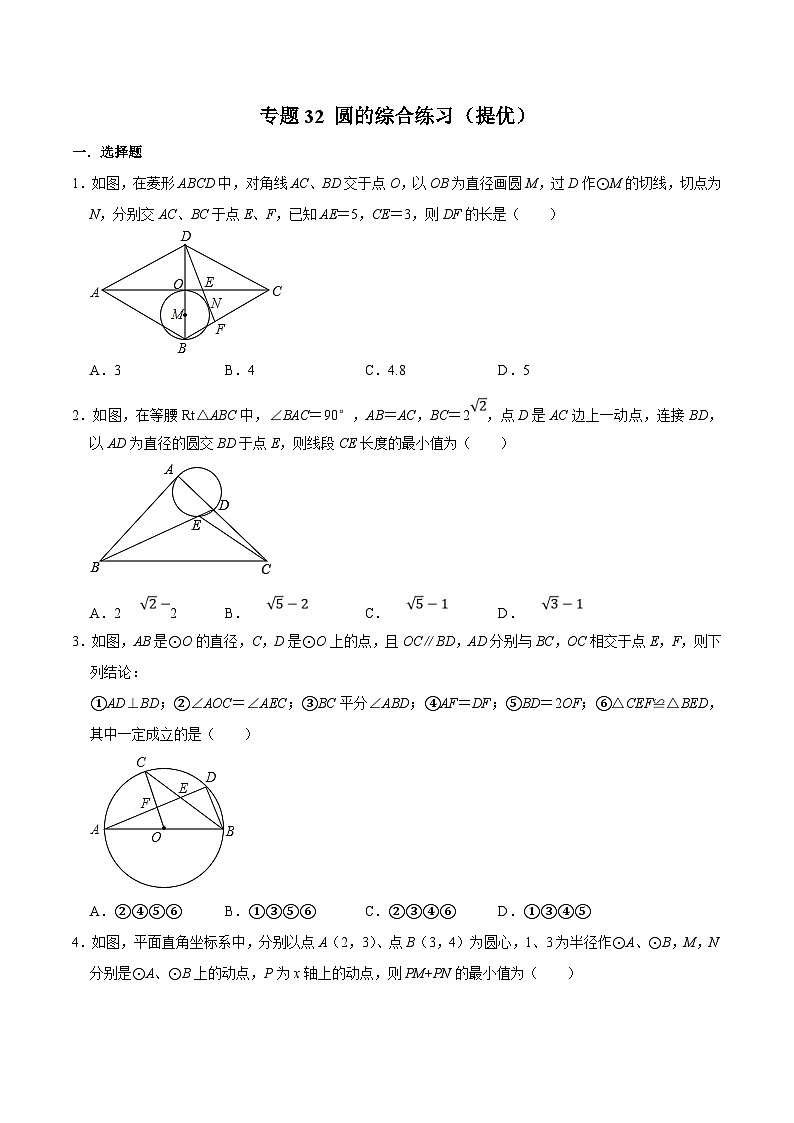
中考数学二轮复习几何专项知识精讲+基础提优训练专题32 圆的综合练习（提优）（2份，原卷版+解析版）

这是一份中考数学二轮复习几何专项知识精讲+基础提优训练专题32 圆的综合练习（提优）（2份，原卷版+解析版），文件包含中考数学二轮复习几何专项知识精讲+基础提优训练专题32圆的综合练习提优-原卷版doc、中考数学二轮复习几何专项知识精讲+基础提优训练专题32圆的综合练习提优-解析版doc等2份试卷配套教学资源，其中试卷共73页， 欢迎下载使用。

A．3B．4C．4.8D．5
【分析】首先延长EF，过点B作直线平行AC和EF相交于P，由菱形的性质，可求得OE的长，证得AC是⊙M的切线，然后由切线长定理，求得EN的长，易证得△DMN∽△DEO，△EFC∽△PFB，然后由相似三角形的对应边成比例，求得答案．
【解答】解：延长EF，过点B作直线平行AC和EF相交于P，
∵AE＝5，EC＝3，
∴AC＝AE+CE＝8，
∵四边形ABCD是菱形，
∴OA＝OCAC＝4，AC⊥BD，
∴OE＝OC﹣CE＝4﹣3＝1，
∵以OB为直径画圆M，
∴AC是⊙M的切线，
∵DN是⊙M的切线，
∴EN＝OE＝1，MN⊥AN，
∴∠DNM＝∠DOE＝90°，
∵∠MDN＝∠EDO，
∴△DMN∽△DEO，
∴DM：MN＝DE：OE，
∵MN＝BM＝OMOB，
∴DM＝OD+OM＝3MN，
∴DE＝3OE＝3，
∵OE∥BP，
∴OD：OB＝DE：EP，
∵OD＝OB，
∴DE＝EP＝3，
∴BP＝2OE＝2，
∵OE∥BP，
∴△EFC∽△PFB，
∴EF：PF＝EC：BP＝3：2，
∴EF：EP＝3：5，
∴EF＝EP1.8，
∴DF＝DE+EF＝3+1.8＝4.8．
故选：C．
【点评】此题属于圆的综合题，考查了切线的判定与性质、菱形的性质以及相似三角形的判定与性质．注意准确作出辅助线是解此题的关键．
2．如图，在等腰Rt△ABC中，∠BAC＝90°，AB＝AC，BC＝2，点D是AC边上一动点，连接BD，以AD为直径的圆交BD于点E，则线段CE长度的最小值为（ ）
A．22B．C．D．
【分析】连接AE，如图1，先根据等腰直角三角形的性质得到AB＝AC＝2，再根据圆周角定理，由AD为直径得到∠AED＝90°，接着由∠AEB＝90°得到点E在以AB为直径的⊙O上，于是当点O、E、C共线时，CE最小，如图2，在Rt△AOC中利用勾股定理计算出OC，从而得到CE的最小值为1．
【解答】解：连接AE，如图1，
∵∠BAC＝90°，AB＝AC，BC＝2，
∴AB＝AC＝2，
∵AD为直径，
∴∠AED＝90°，
∴∠AEB＝90°，
∴点E在以AB为直径的⊙O上，
∵⊙O的半径为1，
连接OE，OC，
∴OEAB＝1
在Rt△AOC中，
∵OA＝1，AC＝2，
∴OC，
由于OC，OE＝1是定值，
点E在线段OC上时，CE最小，如图2，
∴CE＝OC﹣OE1，
即线段CE长度的最小值为1．
故选：C．
【点评】本题考查了圆的综合题：熟练掌握圆周角定理和等腰直角三角形的性质；会利用勾股定理计算线段的长．解决本题的关键是确定E点运动的规律，从而把问题转化为圆外一点到圆上一点的最短距离问题．
3．如图，AB是⊙O的直径，C，D是⊙O上的点，且OC∥BD，AD分别与BC，OC相交于点E，F，则下列结论：
①AD⊥BD；②∠AOC＝∠AEC；③BC平分∠ABD；④AF＝DF；⑤BD＝2OF；⑥△CEF≌△BED，其中一定成立的是（ ）
A．②④⑤⑥B．①③⑤⑥C．②③④⑥D．①③④⑤
【分析】①由直径所对圆周角是直角，
②由于∠AOC是⊙O的圆心角，∠AEC是⊙O的圆内部的角，
③由平行线得到∠OCB＝∠DBC，再由圆的性质得到结论判断出∠OBC＝∠DBC；
④用半径垂直于不是直径的弦，必平分弦；
⑤用三角形的中位线得到结论；
⑥得不到△CEF和△BED中对应相等的边，所以不一定全等．
【解答】解：①、∵AB是⊙O的直径，
∴∠ADB＝90°，
∴AD⊥BD，
②假设∠AOC＝∠AEC，
∴∠A＝∠C，
∵∠ABC＝∠C，
∴∠A＝∠ABC，
∴，
∵OC∥BD
∴∠C＝∠CBD，
∴∠ABC＝∠DBC，
即：
∴C，D是半圆的三等分点，
而与“C，D是⊙O上的点”矛盾，
∴∠AOC≠∠AEC，
③、∵OC∥BD，
∴∠OCB＝∠DBC，
∵OC＝OB，
∴∠OCB＝∠OBC，
∴∠OBC＝∠DBC，
∴BC平分∠ABD，
④、∵AB是⊙O的直径，
∴∠ADB＝90°，
∴AD⊥BD，
∵OC∥BD，
∴∠AFO＝90°，
∵点O为圆心，
∴AF＝DF，
⑤、由④有，AF＝DF，
∵点O为AB中点，
∴OF是△ABD的中位线，
∴BD＝2OF，
⑥∵△CEF和△BED中，没有相等的边，
∴△CEF与△BED不全等，
故选：D．
【点评】此题是圆综合题，主要考查了圆的性质，平行线的性质，角平分线的性质，解本题的关键是熟练掌握圆的性质．
4．如图，平面直角坐标系中，分别以点A（2，3）、点B（3，4）为圆心，1、3为半径作⊙A、⊙B，M，N分别是⊙A、⊙B上的动点，P为x轴上的动点，则PM+PN的最小值为（ ）
A．54B．1C．6﹣2D．
【分析】作⊙A关于x轴的对称⊙A′，连接BA′分别交⊙A′和⊙B于M、N，交x轴于P，如图，根据两点之间线段最短得到此时PM+PN最小，再利用对称确定A′的坐标，接着利用两点间的距离公式计算出A′B的长，然后用A′B的长减去两个圆的半径即可得到MN的长，即得到PM+PN的最小值．
【解答】解：作⊙A关于x轴的对称⊙A′，连接BA′分别交⊙A′和⊙B于M、N，交x轴于P，如图，
则此时PM+PN最小，
∵点A坐标（2，3），
∴点A′坐标（2，﹣3），
∵点B（3，4），
∴A′B5，
∴MN＝A′B﹣BN﹣A′M＝53﹣1＝54，
∴PM+PN的最小值为54．
故选：A．
【点评】本题考查了圆的综合题：掌握与圆有关的性质和关于x轴对称的点的坐标特征；会利用两点之间线段最短解决线段和的最小值问题；会运用两点间的距离公式计算线段的长；理解坐标与图形性质．
5．如图，已知直线yx﹣3与x轴、y轴分别交于A、B两点，P是以C（0，1）为圆心，1为半径的圆上一动点，连接PA、PB．则△PAB面积的最大值是（ ）
A．8B．12C．D．
【分析】求出A、B的坐标，根据勾股定理求出AB，求出点C到AB的距离，即可求出圆C上点到AB的最大距离，根据面积公式求出即可．
【解答】解：∵直线yx﹣3与x轴、y轴分别交于A、B两点，
∴A点的坐标为（4，0），B点的坐标为（0，﹣3），3x﹣4y﹣12＝0，
即OA＝4，OB＝3，由勾股定理得：AB＝5，
过C作CM⊥AB于M，连接AC，
则由三角形面积公式得：AB×CMOA×OCOA×OB，
∴5×CM＝4×1+3×4，
∴CM，
∴圆C上点到直线yx﹣3的最大距离是1，
∴△PAB面积的最大值是5，
故选：C．
【点评】本题考查了三角形的面积，点到直线的距离公式的应用，解此题的关键是求出圆上的点到直线AB的最大距离，属于中档题目．
6．如图，AB是⊙O的直径，点C是⊙O上一点，AD与过点C的切线垂直，垂足为D，直线DC与AB的延长线交于点P，弦CE平分∠ACB，交AB于点F，连接BE，BE＝7．下列四个结论：①AC平分∠DAB；②PF2＝PB•PA；③若BCOP，则阴影部分的面积为π；④若PC＝24，则tan∠PCB．其中正确的是（ ）
A．①②B．③④C．①②④D．①②③
【分析】①连接OC，根据切线的性质可得OC⊥CD，则AD∥OC，根据等边对等角，以及平行线的性质即可证得；
②根据圆周角定理以及三角形的外角的性质定理证明∠PFC＝∠PCF，根据等角对等边即可证得PC＝PF，又由∠PCB＝∠PAC，∠P＝∠P，可证得△PCB∽△PAC，然后由相似三角形的对应边成比例，证得结论；
③首先连接AE，由圆周角定理与弦CE平分∠ACB，可得△ABE是等腰直角三角形，继而求得直径AB的长，由BCOP，可得BC是中线，△OBC是等边三角形，继而求得阴影部分的面积；
④在直角△POC中利用勾股定理即可列方程求得PB的长，由△PCB∽△PAC，根据相似三角形的性质求得PB与PC的比值，即可求得tan∠PCB．
【解答】解：①连接OC．
∵OA＝OC，
∴∠OAC＝∠OCA．
∵PC是⊙O的切线，AD⊥CD，
∴∠OCP＝∠D＝90°，
∴OC∥AD．
∴∠CAD＝∠OCA＝∠OAC．
即AC平分∠DAB．故正确；
②∵AB是直径，
∴∠ACB＝90°，
∴∠PCB+∠ACD＝90°，
又∵∠CAD+∠ACD＝90°，
∴∠CAB＝∠CAD＝∠PCB．
又∵∠ACE＝∠BCE，∠PFC＝∠CAB+∠ACE，∠PCF＝∠PCB+∠BCE．
∴∠PFC＝∠PCF．
∴PC＝PF，
∵∠P是公共角，
∴△PCB∽△PAC，
∴PC：PA＝PB：PC，
∴PC2＝PB•PA，
即PF2＝PB•PA；故正确；
③连接AE．
∵∠ACE＝∠BCE，
∴，
∴AE＝BE．
又∵AB是直径，
∴∠AEB＝90°．
∴ABBE714，
∴OB＝OC＝7，
∵PD是切线，
∴∠OCP＝90°，
∵BCOP，
∴BC是Rt△OCP的中线，
∴BC＝OB＝OC，
即△OBC是等边三角形，
∴∠BOC＝60°，
∴S△BOC，S扇形BOCπ×72π，
∴阴影部分的面积为π；故错误；
④∵△PCB∽△PAC，
∴，
∴tan∠PCB＝tan∠PAC，
设PB＝x，则PA＝x+14，
∵PC2＝PB•PA，
∴242＝x（x+14），
解得：x1＝18，x2＝﹣32，
∴PB＝18，
∴tan∠PCB；故正确．
故选：C．
【点评】本题属于圆的综合题，考查了圆的切线性质以及解直角三角形的知识．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．
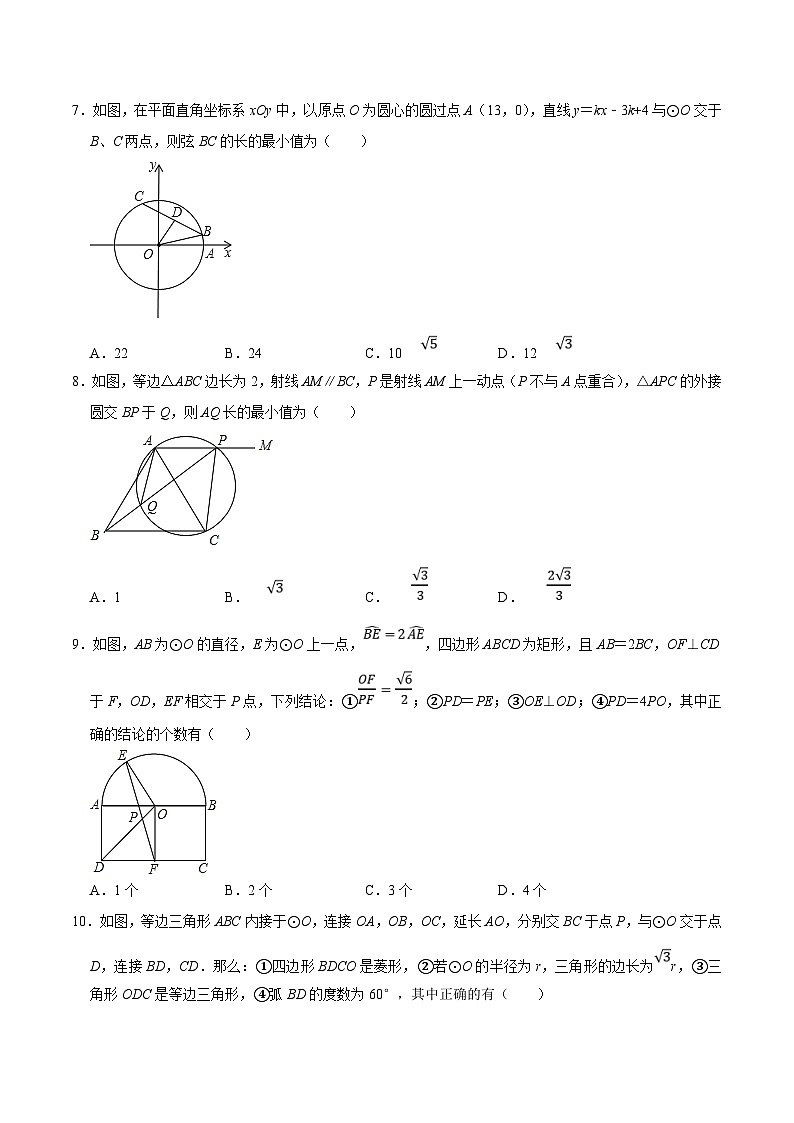
7．如图，在平面直角坐标系xOy中，以原点O为圆心的圆过点A（13，0），直线y＝kx﹣3k+4与⊙O交于B、C两点，则弦BC的长的最小值为（ ）
A．22B．24C．10D．12
【分析】易知直线y＝kx﹣3k+4过定点D（3，4），运用勾股定理可求出OD，由条件可求出半径OB，由于过圆内定点D的所有弦中，与OD垂直的弦最短，因此只需运用垂径定理及勾股定理就可解决问题．
【解答】解：对于直线y＝kx﹣3k+4＝k（x﹣3）+4，当x＝3时，y＝4，
故直线y＝kx﹣3k+4恒经过点（3，4），记为点D．
过点D作DH⊥x轴于点H，
则有OH＝3，DH＝4，OD5．
∵点A（13，0），
∴OA＝13，
∴OB＝OA＝13．
由于过圆内定点D的所有弦中，与OD垂直的弦最短，如图所示，
因此运用垂径定理及勾股定理可得：
BC的最小值为2BD＝222×12＝24．
故选：B．
【点评】本题主要考查了直线上点的坐标特征、垂径定理、勾股定理等知识，发现直线恒经过点（3，4）以及运用“过圆内定点D的所有弦中，与OD垂直的弦最短”这个经验是解决该选择题的关键．
8．如图，等边△ABC边长为2，射线AM∥BC，P是射线AM上一动点（P不与A点重合），△APC的外接圆交BP于Q，则AQ长的最小值为（ ）
A．1B．C．D．
【分析】过点B作BD⊥直线AP，垂足为D，过点C作CE⊥直线AP，垂足为E，易得AD＝AE＝1，BD＝CE，设AP＝x，则DP＝x+1，EP，根据勾股定理可得BP2＝x2+2x+4，CP2＝x2﹣2x+4．易证△AQC∽△PCB，则有，由此可得AQ2＝4，然后将该分式进行恒等变形并运用配方法就可解决问题．
方法二：探究出的Q的运动轨迹，即可解决问题．
【解答】解：过点B作BD⊥直线AP，垂足为D，过点C作CE⊥直线AP，垂足为E，连接QC，如图，
则有BD∥CE．
∵AP∥BC，∠BDE＝90°，
∴四边形BCED是矩形，
∴∠DBC＝∠ECB＝90°．
∵△ABC是等边三角形，
∴AB＝AC＝BC＝2，∠ABC＝∠ACB＝60°，
∴∠DBA＝∠ECA＝30°，
∴AD＝1，AE＝1，
∴BD，CE．
设AP＝x，则DP＝x+1，EP．
在Rt△BDP中，BP2＝BD2+DP2＝3+（x+1）2＝x2+2x+4．
在Rt△CEP中，CP2＝CE2+EP2＝3+（x﹣1）2＝x2﹣2x+4．
∵AM∥BC，
∴∠APB＝∠CBP．
∵∠APB＝∠ACQ，
∴∠ACQ＝∠CBP．
∵∠QAC＝∠CPB，
∴△AQC∽△PCB，
∴，
∴AQ＝2，
∴AQ2＝44
＝4×（1）
＝4×（1）
＝4，
当0即x＝2时，AQ2取到最小值为，此时AQ．
故选D．
方法二：如图，
易知∠PQC＝∠PAC＝∠ACB＝60°，
∴∠BQC＝120°，
∴点Q的运动轨迹是，
∴当AQ⊥BC时，AQ的长最小，设AQ交BC于G，此时AG，OGBQAQ，
∴AQ的最小值为，
故选：D．
【点评】本题主要考查了圆周角定理、平行线的性质、等边三角形的性质、矩形的判定与性质、相似三角形的判定与性质、勾股定理、30°角所对的直角边等于斜边的一半等知识，将分式进行恒等变形并运用配方法是解决本题的关键，寻找点Q的运动轨迹是方法二的突破点．
9．如图，AB为⊙O的直径，E为⊙O上一点，，四边形ABCD为矩形，且AB＝2BC，OF⊥CD于F，OD，EF相交于P点，下列结论：①；②PD＝PE；③OE⊥OD；④PD＝4PO，其中正确的结论的个数有（ ）
A．1个B．2个C．3个D．4个
【分析】过E作EN垂直DC交AB于点M，设EF与AB交于点H，设圆的半径为R，根据题意，，可得出∠AOE＝60°，继而求得EM、MO的长度，根据三角形的相似定理可求得MH，继而得出OH，利用相似三角形的性质可分别求出OP、DP、HP、PF，这样即可判断各结论正确与否．
【解答】解：
过E作EN垂直DC交AB于点M，设圆的半径为R，
∵AB为⊙O的直径，，
∴∠AOE＝60°，
∵EN⊥DC，四边形ABCD为矩形，
∴EN⊥AB，
在Rt△EMO中，∠AOE＝60°，则∠OEM＝30°，
∴OMR，EMR，
易得四边形OMNF为矩形，则MN＝OF＝BCAB＝R，
∴NF＝OFR，
∵△EMH∽△ENF，
∴，即，
解得：MHR，则OH＝OM﹣MH＝（2）R，
在Rt△OHF中，HF（）R，
∵△OPH∽△DPF，
∴2，
∵HP+PF＝HF＝（）R，
∴HP＝（）R，PFR，
∴，故①正确；
同理可得：OPR，PDR，
在Rt△EMH中，EH，
则EP＝EH+HP＝DPR，故②正确；
∠AOE+∠AOD＝60°+45°＝105°，故③错误；
2，故④错误．
综上可得①②正确，共2个．
故选：B．
【点评】本题属于圆的综合题，涉及了相似三角形的判定与性质、矩形的性质、勾股定理，综合考察的知识点较多，解答本题要求同学们熟练掌握所学知识点，并灵活运用，难度较大．
10．如图，等边三角形ABC内接于⊙O，连接OA，OB，OC，延长AO，分别交BC于点P，与⊙O交于点D，连接BD，CD．那么：①四边形BDCO是菱形，②若⊙O的半径为r，三角形的边长为r，③三角形ODC是等边三角形，④弧BD的度数为60°，其中正确的有（ ）
A．1个B．2个C．3个D．4个
【分析】证明△ABO≌△ACO，可得∠BAD＝∠CAD＝30°，从而可得BD＝CDAO，可判断①正确；在Rt△ABD中，根据BD＝OB＝r，∠BAD＝30°，可求出AB，从而判断②正确；由①可得OC＝OD＝CD，从而判断③正确；求出∠BOD的度数，即可判断④正确；
【解答】解：∵△ABC是等边三角形，
∴AB＝AC＝BC，
在△ABO和△ACO中，
∵，
∴△ABO≌△ACO（SSS），
∴∠BAD＝∠CAD＝30°，
则在Rt△ABD中，BDAD＝OB，
同理CDAD＝OB，
∵OB＝OC＝BD＝CD，
∴四边形BDCO是菱形，故①正确；
在Rt△ABD中，AD＝2r，BD＝r，
∴ABr，故②正确；
∵CO＝OD＝CD，
∴△ODC是等边三角形，故③正确；
∠BOD＝2∠BAD＝60°，
∴弧BD的度数为60°，故④正确．
综上可得：①②③④均正确，共4个．
故选：D．
【点评】本题考查了圆的综合，涉及了圆周角定理、等边三角形的性质、解直角三角形及全等三角形的判定与性质，综合性较强，解答本题的关键是掌握各知识点的内容，灵活运用．
11．如图，△ABC内接于⊙O，∠BAC＝60°，AD⊥BC于D，交⊙O于F，BE⊥AC于E，BE交AD于H，直线OH交AB于M，交AC于N，下列结论中：
（1）DH＝DF；（2）AO＝AH；（3）AM＝AN；（4）MO＝OH＝HN．
其中正确的是（ ）
A．（1）（2）（3）B．（1）（2）（4）C．（1）（3）（4）D．（2）（3）（4）
【分析】连接CH、CF．延长CH交AB于Q，根据H是垂心求出∠HCD＝∠FCD，根据ASA证△HCD≌△FCD，推出DH＝DF即可判断（1）；作OP⊥AB于P，连接OB，根据圆周角定理求出∠AOP＝∠ACB，求出∠PAO＝∠EAH，求出AP＝AEAB，根据ASA证△AEH≌△APO，即可推出AO＝AH，即可判断（2）；过A作AR⊥OH于R，求出∠MAR＝∠NAR，根据ASA证△MAR≌△NAR，推出AM＝AN，即可判断（3）；根据等腰三角形的性质三线合一定理推出OM＝HN，但不能推出OH和OM或HN的关系，即可判断（4）．
【解答】解：连接CH、CF．延长CH交AB于Q，
∵BE⊥AC，AD⊥BC，BE交AD于H，
∴H是垂心，
∴CQ⊥AB，∠ADC＝∠CDF＝90°，
∴∠BCH+∠ABC＝90°，
∵∠BCF+∠AFC＝90°，∠ABC＝∠AFC，
∴∠BCH＝∠BCF，
在△DCH和△DCF中
∵，
∴△CDH≌△CDF（ASA）
∴HD＝DF，∴（1）正确；
作OP⊥AB于P，
∵∠BAC＝60°，∠BEA＝90°，
∴∠ABE＝30°，
∴AEAB，
∵OP⊥AB，OP过O点，
∴APAB（垂径定理），
∴AE＝AP，
∵∠AOP＝∠ACB，∠BAO+∠AOP＝90°，∠ACD＝90°，
∴∠CAF+∠ACB＝90°，
∴∠BAO＝∠CAF，
在△AEH和△APO中
∵，
∴△AEH≌△APO（ASA），
∴AO＝AH，∠BAO＝∠CAF，∴（2）正确；
过A作AR⊥OH于R，
即∠ARM＝∠ARN＝90°，
∵AO＝AH，
∴∠OAR＝∠HAR，
∵∠MAO＝∠EAH，
∴∠MAR＝∠NAR，
在△MAR和△NAR中
∵，
∴△MAR≌△NAR（ASA），
∴AM＝AN，∴（3）正确；
∵AM＝AN，AH＝AO，AR⊥MN，
∴MR＝NR，OR＝RH，
∴OM＝HN，
根据已知条件不能推出OH和OM的关系，∴（4）错误；
故选：A．
【点评】本题考查了等腰三角形性质，全等三角形的性质和判定，圆周角定理，含30度角的直角三角形，垂径定理等知识点，此题综合性比较强，难度偏大．
12．已知，如图，△ABC内接于⊙O，∠BAC＝60°，高线AD，BE相交于H，直线OH与AB，AC分别交于Q，P．下列结论：①∠BAO＝∠CAD；②AH＝AO；③△AQP是等腰三角形；④若∠NAB＝∠MAC＝15°，则．其中正确的有（ ）
A．1个B．2个C．3个D．4个
【分析】延长AO交⊙O于点F，连接BF，如图1，根据圆周角定理就可推出①正确；易证△ABF∽△AEH，从而有，再由∠BAC＝60°可推出AB＝2AE，从而得到AF＝2AH，进而得到②正确；易证△AOQ≌△AHP，从而有AQ＝AP，从而得到③正确；作∠BAC的角平分线交⊙O于点T，过点T作TG⊥AN，垂足为G，过点T作TK⊥AM，垂足为K，连接TN，TM；过点T作TS⊥AB，垂足为S，过点T作TR⊥AC，垂足为R，连接TB，TC；如图2，可以证到Rt△NGT≌Rt△MKT（HL），进而可以证到AN+AM＝2AK，同理可得；AB+AC＝2AR．而AK＝AT•cs∠KATAT，AR＝AT•cs∠RATAT．即可证得④正确．
【解答】解：延长AO交⊙O于点F，连接BF，如图1，
∵AF是⊙O的直径，
∴∠ABF＝90°．
∴∠BAF+∠F＝180°．
∵AD⊥BC，
∴∠ADC＝90°．
∴∠DAC+∠C＝90°．
∵∠F＝∠C，
∴∠BAF＝∠DAC，即∠BAO＝∠CAD．
故①正确．
∵BE⊥AC，
∴∠BEA＝90°．
∴∠ABF＝∠AEH．
∵∠BAF＝∠HAE，
∴△ABF∽△AEH．
∴．
∵∠BEA＝90°，∠BAE＝60°，
∴∠ABE＝30°．
∴AB＝2AE．
∴AF＝2AH．
∵AF＝2AO，
∴AO＝AH．
故②正确．
∵AO＝AH，
∴∠AOH＝∠AHO．
∴∠AOQ＝∠AHP．
在△AOQ和△AHP中，
．
∴△AOQ≌△AHP．
∴AQ＝AP．
∴△AQP是等腰三角形．
故③正确．
作∠BAC的角平分线交⊙O于点T，
过点T作TG⊥AN，垂足为G，过点T作TK⊥AM，垂足为K，连接TN，TM；
过点T作TS⊥AB，垂足为S，过点T作TR⊥AC，垂足为R，连接TB，TC；如图2，
∵AT平分∠BAC，∴∠BAT＝∠CAT∠BAC＝30°．
∵∠NAB＝∠MAC＝15°，∴∠NAT＝∠MAT＝45°．
∵∠NAT＝∠MAT，TG⊥AN，TK⊥AM，
∴TG＝TK，TN＝TM．
∴AGAK．
在Rt△NGT和Rt△MKT中，
．
∴Rt△NGT≌Rt△MKT（HL）．
∴NG＝MK．
∴AN+AM＝AG+GN+AK﹣MK＝2AK．
同理可得；AB+AC＝2AR．
在Rt△AKT中，
AK＝AT•cs∠KAT＝AT•cs45°AT．
在Rt△ART中，
AR＝AT•cs∠RAT＝AT•cs30°AT．
∴．
故④正确．
故选：D．
【点评】本题考查了圆周角定理、相似三角形的判定与性质、全等三角形的判定与性质、特殊角的三角函数值、30°角所对的直角边等于斜边的一半、角平分线的性质、勾股定理等知识，综合性强，有一定的难度，而通过添加辅助线证到AN+AM＝2AK，AB+AC＝2AR是证明④是真命题的关键．
二．填空题
13．如图，在平面直角坐标系中，Q（3，4），P是在以Q为圆心，2为半径的⊙Q上一动点，A（1，0）、B（﹣1，0），连接PA、PB，则PA2+PB2的最小值是 20 ．
【分析】设点P（x，y），表示出PA2+PB2的值，从而转化为求OP的最值，画出图形后可直观得出OP的最值，代入求解即可．
【解答】解：设P（x，y），
∵PA2＝（x﹣1）2+y2，PB2＝（x+1）2+y2，
∴PA2+PB2＝2x2+2y2+2＝2（x2+y2）+2，
∵OP2＝x2+y2，
∴PA2+PB2＝2OP2+2，
当点P处于OQ与圆的交点上时，OP取得最值，
∴OP的最小值为OQ﹣PQ＝5﹣2＝3，
∴PA2+PB2最小值为20．
故答案为：20．
【点评】本题考查了圆的综合，解答本题的关键是设出点P坐标，将所求代数式的值转化为求解OP的最小值，难度较大．
14．已知半径为5的⊙O1过点O（0，0），A（8，0），与y轴的正半轴交于点B，OE为直径，点M为弧OBE上一动点（不与点O、E重合），连接MA，作NA⊥MA于点A交ME的延长线于点N，则线段AN最长为 ．
【分析】先判断出∠OAE＝90°，根据勾股定理得出AE＝6，再判断出△OAE∽△MAN得出ANAM，即AM是直径时AM最大即可得出结论．
【解答】解：如图，连接AE，∵A（8，0），
∴OA＝8，
∵⊙O1的半径为5，OE是⊙O1的直径，
∴OE＝10，
∵OE是⊙O1的直径，
∴∠OAE＝90°，
在Rt△OAE中，根据勾股定理得，AE6，
∵NA⊥MA，
∴∠NAM＝∠OAE＝90°，
∵∠AOE＝∠AMN，
∴△OAE∽△MAN，
∴，
∴ANAMAM，要AN最长，
则有AM最长，而AM是⊙O1的弦，
∴AM最大是直径为10，
∴AN最大AM最大10，
故答案为．
【点评】此题是圆的综合题，主要考查了圆的性质，勾股定理，相似三角形的判定和性质，作出辅助线判断出△OAE∽△MAN是解本题的关键．
15．在⊙O的内接四边形ABCD中，AB＝6，AD＝10，∠BAD＝60°，点C为弧BD的中点，则AC的长是 ．
【分析】将△ACD绕点C逆时针旋转120°得△CBE，根据旋转的性质得出∠E＝∠CAD＝30°，BE＝AD＝5，AC＝CE，求出A、B、E三点共线，解直角三角形求出即可；过C作CE⊥AB于E，CF⊥AD于F，得出∠E＝∠CFD＝∠CFA＝90°，推出，求出∠BAC＝∠DAC，BC＝CD，求出CE＝CF，根据圆内接四边形性质求出∠D＝∠CBE，证△CBE≌△CDF，推出BE＝DF，证△AEC≌△AFC，推出AE＝AF，设BE＝DF＝x，得出5＝x+3+x，求出x，解直角三角形求出即可．
【解答】解法一、∵A、B、C、D四点共圆，∠BAD＝60°，
∴∠BCD＝180°﹣60°＝120°，
∵∠BAD＝60°，AC平分∠BAD，
∴∠CAD＝∠CAB＝30°，
如图1中，将△ACD绕点C逆时针旋转120°得△CBE，
则∠E＝∠CAD＝30°，BE＝AD＝10，AC＝CE，
∴∠ABC+∠EBC＝（180°﹣CAB﹣∠ACB）+（180°﹣∠E﹣∠BCE）＝180°，
∴A、B、E三点共线，
过C作CM⊥AE于M，
∵AC＝CE，
∴AM＝EM（6+10）＝8，
在Rt△AMC中，AC；
解法二、如图2中，过C作CE⊥AB于E，CF⊥AD于F，
则∠E＝∠CFD＝∠CFA＝90°，
∵点C为弧BD的中点，
∴，
∴∠BAC＝∠DAC，BC＝CD，
∵CE⊥AB，CF⊥AD，
∴CE＝CF，
∵A、B、C、D四点共圆，
∴∠D＝∠CBE，
在△CBE和△CDF中
，
∴△CBE≌△CDF，
∴BE＝DF，
在△AEC和△AFC中，
，
∴△AEC≌△AFC，
∴AE＝AF，
设BE＝DF＝x，
∵AB＝6，AD＝10，
∴AE＝AF＝x+3，
∴10﹣x＝6+x，
解得：x＝2，
即AE＝8，
∴AC，
故答案为 ．
【点评】本题考查了圆心角、弧、弦之间的关系，圆内接四边形性质，解直角三角形，全等三角形的性质和判定的应用，能正确作出辅助线是解此题的关键，综合性比较强，难度适中，属于中考填空题中的压轴题．
16．对于一个矩形ABCD及⊙M给出如下定义：在同一平面内，如果矩形ABCD的四个顶点到⊙M上一点的距离相等，那么称这个矩形ABCD是⊙M的“伴侣矩形”．如图，在平面直角坐标系xOy中，直线l：yx﹣3交x轴于点M，⊙M的半径为2，矩形ABCD沿直线运动（BD在直线l上），BD＝2，AB∥y轴，当矩形ABCD是⊙M的“伴侣矩形”时，点C的坐标为 （，）或（，） ．
【分析】根据“伴侣矩形”的定义可知：圆上的点一定在矩形的对角线交点上，因为只有对角线交点到四个顶点的距离相等，由此画出图形，先求出直线与x轴和y轴两交点的坐标和矩形的长和宽；
有两种情况：①矩形在x轴下方时，作辅助线构建相似三角形得比例式，分别求出DG和DH的长，从而求出CG的长，根据坐标特点写出点C的坐标；②矩形在x轴上方时，也分别过C、B两点向两坐标轴作垂线，利用平行相似得比例式，求出：C（，）．
【解答】解：如图所示，矩形在这两个位置时就是⊙M的“伴侣矩形”，
根据直线l：yx﹣3得：OM，ON＝3，
由勾股定理得：MN2，
①矩形在x轴下方时，分别过A、D作两轴的垂线AH、DG，
由cs∠ABD＝cs∠ONM，
∴，AB，则AD＝1，
∵DG∥y轴，
∴△MDG∽△MNO，
∴，
∴，
∴DG，
∴CG，
同理可得：，
∴，
∴DH，
∴C（，）；
②矩形在x轴上方时，同理可得：C（，）；
故答案为：（，）或（，）．
【点评】此题主要考查了圆的综合应用以及相似三角形的性质和矩形等知识，综合性较强，解答本题需要我们熟练各部分的内容，对学生的综合能力要求较高，一定要注意将所学知识贯穿起来．同时，正确理解题意准确画出符合条件的矩形是本题的关键，这就需要熟练掌握矩形的对角线的交点到四个顶点的距离相等．
17．如图，点A（2，0），以OA为半径在第一象限内作圆弧AB，使∠AOB＝60°，点C为弧AB的中点，D为半径OA上一动点（不与点O，A重合），点A关于直线CD的对称点为E，若点E落在半径OA上，则点E的坐标为 （） ；若点E落在半径OB上，则点E的坐标为 （，） ．
【分析】根据点E落在半径OA上．可以画出相应的图形，可知点A与点E关于点CD对称，从而可以得到DE＝DA，由点C为弧AB的中点，∠AOB＝60°，OC＝OA＝2，可以求得OD和AD的长，从而可以求得OE的长，进而得到点E的坐标；
根据点E落在半径OB上，画出相应的图形，由D为半径OA上一动点（不与点O，A重合），点A关于直线CD的对称点为E，可知CB＝CE，由前面求得的OE的长与此时OE的长相等，根据∠AOB＝60°，可以求得点E的坐标．
【解答】解：当点E落在半径OA上时，连接OC，如下图1所示，
∵∠ADC＝90°，∠AOB＝60°，点C为弧AB的中点，点A（2，0），
∴∠COD＝30°，OA＝OC＝2，
∴CD＝OC•sin30°＝2，
∴OD＝OC，
∴AD＝OA﹣OD＝2，
∵DE＝DA，
∴OE＝OD﹣OE（2）＝2，
即点E的坐标为（2，0）；
当点E落在半径OB上时，连接OC，CD，如图2所示，
由已知可得，CE＝CA＝CB，
由上面的计算可知，OE＝2，
∴点E的横坐标为：，
点E的纵坐标为：（2）×sin60°＝3，
故答案为：（，0）；（）．
【点评】本题考查圆的综合题、特殊角的三角函数值，解题的关键是明确题意，画出相应的图形，找出所求问题需要的条件，利用数形结合的思想解答问题．
18．如图，已知⊙O经过点A（2，0）、C（0，2）．直线y＝kx（k≠0）与⊙O分别交于点B、D，则四点A、B、C、D组成的四边形面积的最大值为 4 ．
【分析】分类讨论：当k＜0，如图1，作BE⊥y轴于E，DF⊥x轴于F，设∠AOD＝α，则∠EBO＝α，利用三角函数的定义可得DF＝2sinα，BE＝2csα，则根据三角形面积公式得到S四边形ADBC＝S△AOD+S△BOC+S△AOC＝2sinα+2csα+2，利用三角公式得到S四边形ADBC＝2sin（45°+α）+2，利用正弦的性质得sin（45°+α）≤1，于是可得此时S四边形ADBC的最大值为22；当k＞0，如图2，作BE⊥y轴于E，DF⊥x轴于F，设∠AOD＝α，则∠EBO＝α，同理可得DF＝2sinα，OF＝2csα，BE＝2csα，OE＝2sinα，根据三角形面积公式得S四边形ABCD＝S△AOB+S△AOD+S△DOC+S△BOC＝4sinα+4csα，同样可得S四边形ABCD＝4sin（45°+α），由于sin（45°+α）≤1，则可得到S四边形ADBC的最大值为4，综上所述，四点A、B、C、D组成的四边形面积的最大值为4．
【解答】解：当k＜0，如图1，作BE⊥y轴于E，DF⊥x轴于F，设∠AOD＝α，则∠EBO＝α，
∵⊙O经过点A（2，0）、C（0，2），
∴⊙O的半径为2，
在Rt△OFD中，∵sin∠FOD，
∴DF＝2sinα，
同理可得BE＝2csα，
S四边形ADBC＝S△AOD+S△BOC+S△AOC
•2•2sinα•2•csα•2•2
＝2sinα+2csα+2
＝2（sinαcsα）+2
＝2（sin45°•csα+cs45°•sinα）+2
＝2sin（45°+α）+2，
∵sin（45°+α）≤1，
∴S四边形ADBC≤22，即此时S四边形ADBC的最大值为22；
当k＞0，如图2，作BE⊥y轴于E，DF⊥x轴于F，设∠AOD＝α，则∠EBO＝α，
同理可得DF＝2sinα，OF＝2csα，BE＝2csα，OE＝2sinα，
S四边形ABCD＝S△AOB+S△AOD+S△DOC+S△BOC
•2•2sinα•2•sinα•2•csα•2•csα
＝4sinα+4csα
＝4（sinαcsα）
＝2（sin45°•csα+cs45°•sinα）
＝4sin（45°+α）
∵sin（45°+α）≤1，
∴S四边形ADBC≤4，即此时S四边形ADBC的最大值为4，
综上所述，四点A、B、C、D组成的四边形面积的最大值为4．
故答案为4．
【点评】本题考查了圆的综合题：熟练掌握圆的有关性质和一次函数的性质；理解坐标与图形性质；学会构造直角三角形和解直角三角形；会运用三角函数公式．
19．如图，已知△ABC，AC＝BC，∠C＝90°．O是AB的中点，⊙O与AC，BC分别相切于点D与点E．点F是⊙O与AB的一个交点，连DF并延长交CB的延长线于点G．则∠CDG＝ 67.5° ，若AB，则BG＝ 22 ．
【分析】连接OD，由AC为圆O的切线，根据切线的性质得到OD与AC垂直，又AC＝BC，且∠C＝90°，得到三角形ABC为等腰直角三角形，得到∠A＝45°，在直角三角形ABC中，由AC与BC的长，根据AB的长，又O为AB的中点，从而得到AO等于BO都等于AB的一半，求出AO与BO的长，再由OB﹣OF求出FB的长，同时由OD和GC都与AC垂直，得到OD与GC平行，得到一对内错角相等，再加上对顶角相等，由两对对应角相等的两三角形相似得到三角形ODF与三角形GBF相似，由相似得比例，把OD，OF及FB的长代入即可求出GB的长．
【解答】解：连接OD．
∵CD切⊙O于点D，
∴∠ODA＝90°，∠DOA＝45°，
∵OD＝OF，
∴∠ODF＝∠OFD∠DOA＝22.5°，
∴∠CDG＝∠CDO﹣∠ODF＝90°﹣22.5°＝67.5°．
∵AC为圆O的切线，
∴OD⊥AC，
又O为AB的中点，∴AO＝BOAB＝2，
∴圆的半径DO＝FO＝AOsinA＝22，
∴BF＝OB﹣OF＝22．
∵GC⊥AC，OD⊥AC，
∴OD∥CG，
∴∠ODF＝∠G，又∠OFD＝∠BFG，
∴△ODF∽△BGF，
∴，即，
∴BG＝22．
故答案为：67.5°，22．
【点评】此题考查了切圆的综合知识．在运用切线的性质时，若已知切点，连接切点和圆心，得垂直；若不知切点，则过圆心向切线作垂直，即“知切点连半径，无切点作垂直”．圆与相似三角形，及三角函数相融合的解答题、与切线有关的性质与判定有关的证明题是近几年中考的热点，故要求学生把所学知识融汇贯穿，灵活运用．
20．如图，在平面直角坐标系xOy中，点A的坐标为（4，0），以点A为圆心，4为半径的圆与x轴交于O，B两点，OC为弦，∠AOC＝60°，当点P在直径OB上运动时，连CP并延长与⊙A相交于点Q，PO＝ 2或2+2 时，△OCQ是等腰三角形．
【分析】本题分两种情况：
①以O为顶点，OC，OQ为腰．那么可过C作x轴的垂线，交圆于Q，此时三角形OCQ就是此类情况所说的等腰三角形；那么此时PO可在直角三角形OCP中，根据∠COA的度数，和OC即半径的长求出PO．
②以Q为顶点，QC，QD为腰，那么可做OC的垂直平分线交圆于Q，则这条线必过圆心，如果设垂直平分线交OC于D的话，可在直角三角形AOQ中根据∠QAE的度数和半径的长求出Q的坐标；然后用待定系数法求出CQ所在直线的解析式，得出这条直线与x轴的交点，也就求出了PO的值．
【解答】解：①过点C作CP1⊥OB，垂足为P1，延长CP1交⊙A于Q1；如图①，
∵OA是半径，
∴，
∴OC＝OQ1，
∴△OCQ1是等腰三角形；
又∵△AOC是等边三角形，
∴P1OOA＝2；
②过A作AD⊥OC，垂足为D，延长DA交⊙A于Q2，CQ2与x轴交于P2；如图②，
∵A是圆心，
∴DQ2是OC的垂直平分线，
∴CQ2＝OQ2，
∴△OCQ2是等腰三角形；
过点Q2作Q2E⊥x轴于E，
在Rt△AQ2E中，
∵∠Q2AE＝∠OAD∠OAC＝30°，
∴Q2EAQ2＝2，AE＝2，
∴点Q2的坐标（4，﹣2）；
在Rt△COP1中，
∵P1O＝2，∠AOC＝60°，
∴
∴C点坐标（2，）；
设直线CQ2的关系式为y＝kx+b，则
，
解得，
∴y＝﹣x+2+2；
当y＝0时，x＝2+2，
∴P2O＝2+2．
故答案为：2或2+2．
【点评】本题综合考查函数、圆的切线，等边三角形的判定以及垂径定理等知识点．要注意等腰三角形要按顶点和腰的不同来分类讨论．
三．解答题
21．如图，AB是大半圆O的直径．OA是小半圆O1的直径，点C是大半圆O上的一个动点（不与点A、B重合），AC交小半圆O1于点D，DE⊥OC，垂足为E．
（1）求证：AD＝DC；
（2）求证：DE是半圆O1的切线；
（3）如果OE＝EC，请判断四边形O1OED是什么四边形，并证明你的结论．
【分析】（1）连OD可得OD⊥AC，又有OA＝OC，所以第一问可求解；
（2）证明O1D⊥DE即可；
（3）如果OE＝EC，又D为AC的中点，所以四条边相等，再根据角之间的关系，即可得出其形状．
【解答】证明：（1）连接OD，
∵AO为圆O1的直径，
则∠ADO＝90°．
∵AC为⊙O的弦，OD为弦心距，
∴AD＝DC．
（2）证明：∵D为AC的中点，O1为AO的中点，
∴O1D∥OC．
又DE⊥OC，
∴DE⊥O1D
∴DE与⊙O1相切．
（3）如果OE＝EC，又D为AC的中点，
∴DE∥O1O，又O1D∥OE，
∴四边形O1OED为平行四边形．
又∠DEO＝90°，O1O＝O1D，
∴四边形O1OED为正方形．
【点评】此题是圆的综合题，考查了圆周角定理，切线的性质及正方形的判定，熟练掌握切线的性质是解题的关键．
22．如图，Rt△ABC中，∠C＝90°，AC＝BC＝4，P是BC上一点（不与B，C重合），连接AP，将AP绕点A逆时针旋转90°得到AQ，连接BQ，分别交AC，AP于点D，E，作QF⊥AC于点F．
（1）求证：QF＝AC；
（2）若P是BC的中点，求tan∠ADQ的值；
（3）若△AEQ的内心在QF上，直接写出BP的长．
【分析】（1）由旋转的性质得出PA＝PQ，∠PAQ＝90°，则∠PAC+∠QAF＝90°，证明△QAF≌△APC（AAS），由全等三角形的性质得出QF＝AC；
（2）由（1）知，△QAF≌△APC，得出AF＝PC＝2，证明△QDF≌△BDC（AAS），由全等三角形的性质得出DF＝DC＝1，则可得出答案；
（3）证明△QFA≌△QFD（ASA），由全等三角形的性质得出AF＝FD，则可得出答案．
【解答】（1）证明：∵将AP绕点A逆时针旋转90°得到AQ，
∴PA＝PQ，∠PAQ＝90°，
∴∠PAC+∠QAF＝90°，
又∵∠PAC+∠APC＝90°，
∴∠QAF＝∠APC，
∵∠QFA＝∠C＝90°，
∴△QAF≌△APC（AAS），
∴QF＝AC；
（2）解：若P是BC的中点，则PCCB＝2，
由（1）知，△QAF≌△APC，
∴AF＝PC＝2，
∴FC＝2，
∵QF＝AC＝BC，∠QFD＝∠C＝90°，∠QDF＝∠BDC，
∴△QDF≌△BDC（AAS），
∴DF＝DC＝1，
∵QF＝AC＝4，
∴tan．
（3）若△AEQ的内心在QF上，则QF平分∠AQD，
∵QF⊥AC，QF＝QF，
∴△QFA≌△QFD（ASA），
∴AF＝FD，
∵DF＝DC，
∴AF＝FD＝DC，
∴CP＝AF，
∴BP＝4．
【点评】本题是圆的综合题，考查了全等三角形的判定与性质，直角三角形的性质，锐角三角函数，旋转的性质，三角形内心的性质，熟练掌握全等三角形的判定与性质是解题的关键．
23．已知，如图，AB是⊙O的直径，点C为⊙O上一点，OF⊥AC于点F，交⊙O于点E，AC交BE于点H，点D为OE延长线上的一点，且∠ODA＝∠BEC．
（1）求证：AD是⊙O的切线；
（2）求证：CE2＝EH•BE；
（3）若⊙O的半径为5，csB，求AH的长．
【分析】（1）先判断出∠BSC＝∠ODA，进而判断出∠BAC+∠DAF＝90°，即可得出结论；
（2）先判断出∠ACE＝∠CBE，进而判断出△CEH∽△BEC，即可得出结论；
（3）先由三角函数求出BE，进而求出CE＝AE＝6，再借助（2）的结论求出EH，最后用勾股定理求解，即可得出结论．
【解答】（1）证明：∵∠ODA＝∠BEC，∠BEC＝∠BAC，
∴∠BAC＝∠ODA，
∵OF⊥AC，
∴∠AFD＝90°，
∴∠ODA+∠DAF＝90°，
∴∠BAC+∠DAF＝90°，
∴∠OAD＝90°，
∴AB⊥AD，
∵AB是⊙O的直径，
∴AD是⊙O的切线；
（2）如图1，连接BC，
∵OD⊥AC，
∴，
∴∠ECH＝∠EBC，
∵∠CEH＝∠BEC，
∴△CEH∽△BEC，
∴，
∴CE2＝EH•BE；
（3）如图2，连接AE，
∵AB是⊙O的直径，
∴∠AEB＝90°，AB＝10，
在Rt△ABE中，csB，
∴BEAB＝8，根据勾股定理得，AE6，
∵OD⊥AC，
∴CE＝AE＝6，
由（2）知，BE2＝EH•BE，
∴62＝EH×8，
∴EH，
在Rt△AEH中，根据勾股定理得，AH．
【点评】此题是圆的综合题，主要考查了切线的判定判定，垂径定理，相似三角形的判定和性质，勾股定理，锐角三角函数，构造出直角三角形是解本题的关键．
24．如图，Rt△ABC中，∠C＝90°，O为AB上一点，以O为圆心，OB长为半径的圆，与AC相切于点E，交BC于点P，交AB于点H，作EF⊥AB于点F，连接EH，EP．
（1）求证：BE平分∠ABC；
（2）求证：HE•EB＝PB•AE；
（3）若F是AB的中点，AB＝4，求四边形OEPB的周长．
【分析】（1）连接OE，由切线的性质得出∠OEA＝∠ACB＝90°，由平行线的判定得出OE∥BC，则∠OEB＝∠EBC，由等腰三角形的性质得出∠OBE＝∠OEB，则可得出结论；
（2）证明△AHE∽△EPB，由相似三角形的性质得出，则可得出结论；
（3）证明△BEF≌△BEC（AAS），由全等三角形的性质得出BC＝BF，得出∠A＝30°，证明△OBP是等边三角形和△EOP是等边三角形，由等边三角形的性质得出OE＝EP＝PB＝OB，求出PB的长，则可得出答案．
【解答】（1）证明：连接OE，如图1，
∵AC与⊙O相切于点E，
∴∠OEA＝∠ACB＝90°，
∴OE∥BC，
∴∠OEB＝∠EBC，
∵OE＝OB，
∴∠OBE＝∠OEB，
∴∠OBE＝∠EBC，
∴BE平分∠ABC；
（2）证明：∵BH是⊙O的直径，
∴∠BEH＝90°，
∴∠AEH+∠BEC＝90°，
∵∠EBC+∠BEC＝90°，
∴∠AEH＝∠EBC，
∵点B，H，E，P四点在⊙O上，
∴∠BHE+∠EPB＝180°，
又∵∠BHE+∠AHE＝180°，
∴∠AHE＝∠EPB，
∴△AHE∽△EPB，
∴，
∴HE•EB＝PB•AE；
（3）解：由（1）可得：∠ABE＝∠EBC，
∵EF⊥AB，
∴∠EFB＝∠ECB＝90°，
又∵BE＝BE，
∴△BEF≌△BEC（AAS），
∴BC＝BF，
又∵点F是AB的中点，
∴BC＝BFAB＝2，
∴∠A＝30°，
∴∠ABC＝∠AOE＝60°，
连接OP，如图2，
∵OB＝OP，
∴△OBP是等边三角形，
∴∠POB＝60°，
∴∠EOP＝60°，
同理可得△EOP是等边三角形，
∴OE＝EP＝PB＝OB，∠PEC＝30°，
∴PCEP，
∴BP+CPPB＝2，
∴PB，
∴四边形OEPB的周长为．
【点评】此题是圆的综合题，主要考查了圆的性质，切线的性质，圆周角定理，等腰三角形的性质，全等三角形的性质和判定，相似三角形的判定与性质，等边三角形的判定与性质，直角三角形的性质，解本题的关键是熟练掌握相似三角形的判定与性质及圆的性质定理．
25．如图，已知AB是⊙O的直径，点C为⊙O上一点，CD为不过圆心且垂直于AB的弦，CD交AB于点E，连接CO并延长交⊙O于点F，连接CB和DF并延长交于点G．
（1）求证：CF＝GF；
（2）填空：
①当∠BGF＝ 30° 时，四边形BODF为菱形；
②若AB＝6，则△COE面积的最大值是 ．
【分析】（1）先判断出AB∥DF，进而判断出BC＝CG，再判断出BF⊥CG，即可得出结论；
（2）①先判断出△BOF是等边三角形，得出∠BOF＝60°，即可得出结论；
②设出OE＝a，则CE，进而得出S△COE，即可得出结论．
【解答】解：（1）如图，连接BF，
∵CF是直径，
∴∠CBF＝90°，∠CDF＝90°，
∵CD⊥AB，AB为直径，
∴∠CEB＝90°，CE＝DE，
∴∠CEB＝∠CDF＝90°，
∴AB∥DF，
∴CB＝BG，
∴BF是CG的垂直平分线，
∴CF＝GF；
（2）①如图，连接OD，BF，
∵四边形BODF是菱形，
∴OB＝BF，
∵OB＝OF，
∴OB＝OF＝BF，
∴△BOF是等边三角形，
∴∠BOF＝60°，
∴∠BCF∠BOF＝30°，
由（1）知，CF＝GF，
∴∠BGF＝∠BCF＝30°，
故答案为：30°；
②设OE＝a，由（1）知，∠OEC＝90°，
在Rt△COE中，OCAB＝3，
∴CE，
∴S△COECE•OEa，
∴当a2，即a时，S△COE最大，
故答案为：．
【点评】此题是圆的综合题，主要考查了垂径定理，等边三角形的判定和性质，勾股定理，菱形的性质，判断出BF是CG的垂直平分线是解本题的关键．
26．如图，⊙O是△ABC的外接圆，且AB＝AC，点D在弧BC上运动，过点D作DE∥BC，DE交AB的延长线于点E，连接AD、BD．
（1）求证：∠ADB＝∠E；
（2）当AB＝6，BE＝3时，求AD的长？
（3）当点D运动到什么位置时，DE是⊙O的切线？请说明理由．
【分析】（1）先判断出∠ABC＝∠ACB，再判断出∠ADB＝∠ABC，进而得出∠ABC＝∠AED，即可得出结论；
（2）判断出△ABD∽△ADE，得出比例式，即可得出结论．
（3）先判断出AD⊥BC，AD过圆心，进而得出AD⊥ED，即可得出结论．
【解答】证明：∵AB＝AC，
∴∠ABC＝∠ACB，
∵∠ADB＝∠ACB，
∴∠ADB＝∠ABC，
∵DE∥BC，
∴∠ABC＝∠AED，
∴∠ADB＝∠E；
（2）解：由（1）知，∠ADB＝∠E，
∵∠BAD＝∠BAD，
∴△ABD∽△ADE，
∴，
∵AB＝6，BE＝3，
∴，
∴AD＝3，
∴AD的长为3；
（3）当D为的中点时，DE是⊙O的切线，理由为：
∵D为的中点，
∴AD⊥BC，AD过圆心，
∵DE∥BC，
∴AD⊥ED，
∵点D在⊙O上，
∴DE为圆O的切线．
【点评】此题是圆的综合题，主要考查了等腰三角形的性质，平行线的性质，垂径定理，相似三角形的判定和性质，熟练掌握切线的判定方法是解本题的关键．
27．如图，⊙O的直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于点D．
（1）求AD的长；
（2）试探究CA、CB、CD之间的等量关系，并证明你的结论；
（3）连接OD，P为半圆ADB上任意一点，过P点作PE⊥OD于点E，设△OPE的内心为M，当点P在半圆上从点B运动到点A时，求内心M所经过的路径长．
【分析】（1）由圆周角定理得出∠ACB＝∠ADB＝90°，由勾股定理可求出答案；
（2）延长CA到F，使AF＝CB，连接DF，证明△ADF≌△BDC（SAS），由全等三角形的性质得出CD＝FD，∠CDB＝∠FDA，得出∠CDF＝∠ADB＝90°，则△CDF为等腰直角三角形，由等腰直角三角形的性质得出结论；
（3）连接OM，PM，证明△OMD≌△OMP（SAS），由全等三角形的性质得出∠OMD＝∠OMP＝135°，则点M在以OD为弦，并且所对的圆周角为135°的两段劣弧上（分OD左右两种情况），求出OO'的长，由弧长公式可得出答案．
【解答】解：（1）∵AB是⊙O的直径，
∴∠ACB＝∠ADB＝90°，
∵∠ACB的平分线交⊙O于D，
∴∠ACD＝∠BCD＝45°，
∴，
∴AD＝BD，
∴AD2+BD2＝AB2，
∴AD＝BDAB10＝5；
（2）CA+CBCD．
证明如下：延长CA到F，使AF＝CB，连接DF，
∵∠CBD+∠CAD＝180°，∠FAD+∠CAD＝180°，
∴∠CBD＝∠FAD，
在△ADF和△BDC中，
，
∴△ADF≌△BDC（SAS），
∴CD＝FD，∠CDB＝∠FDA，
∴∠CDF＝∠ADB＝90°，△CDF为等腰直角三角形，
∴CA+CB＝CFCD．
（3）连接OM，PM，
∵PE⊥OD，
∴∠PEO＝90°，
∵点M为△OPE的内心，
∴∠OMP＝135°，
在△OMD和△OMP中，
，
∴△OMD≌△OMP（SAS），
∴∠OMD＝∠OMP＝135°，
∴点M在以OD为弦，并且所对的圆周角为135°的两段劣弧上（分OD左右两种情况）：
设弧OMD所在圆的圆心为O'，
∵∠OMD＝135°，
∴∠OO'D＝90°，
∴O'OOD，
∴的长为π，
∴点M的路径长为π．
【点评】此题是圆的综合题，考查了圆周角定理，三角形内心的定义，全等三角形的判定与性质，等腰直角三角形的判定与性质，弧长公式以及勾股定理等知识，熟练掌握圆周角定理和等腰直角三角形的判定与性质是解题的关键．
28．如图，AB是半圆O的直径，点D是半圆O上一点，点C是的中点，CE⊥AB于点E，过点D的切线交EC的延长线于点G，连接AD，分别交CB、CE于点F、P，连接AC．
（1）求证：GP＝GD；
（2）求证：P是线段AF的中点；
（3）连接CD，若CD＝2，BC＝4，求⊙O的半径和CE的长．
【分析】（1）结合切线的性质以及已知得出∠GPD＝∠GDP，进而得出答案；
（2）利用圆周角定理得出PA，PC，PQ的数量关系进而得出答案；
（3）直接利用勾股定理结合三角形面积进而得出答案．
【解答】（1）证明：连接OD，则OD⊥GD，∠OAD＝∠ODA，
∵∠ODA+∠GDP＝90°，∠EAP+∠GPD＝∠EPA+∠EAP＝90°，
∴∠GPD＝∠GDP；
∴GP＝GD；
（2）证明：∵AB 为直径，
∴∠ACB＝90°，
∵CE⊥AB 于E，
∴∠CEB＝90°，
∴∠ACE+∠ECB＝∠ABC+∠ECB＝90°，
∴∠ACE＝∠ABC＝∠CAP，
∴PC＝PA，
∵∠ACB＝90°，
∴∠CQA+∠CAP＝∠ACE+∠PCQ＝90°，
∴∠PCQ＝∠CQA，
∴PC＝PQ，
∴PA＝PQ，即P 为Rt△ACQ 斜边AQ 的中点；
（3）解：连接CD，
∵弧AC＝弧CD，
∴CD＝AC，
∵CD＝2，
∴AC＝2，
∵∠ACB＝90°，
∴AB2，
故⊙O 的半径为，
∵S△ACBCE×ABAC×BC，
∴2CE＝2×4，
∴CE．
【点评】本题属于圆综合题，考查了圆周角定理，垂径定理，圆心角、弧、弦的关系定理，相似三角形的判定与性质，熟练掌握性质及定理是解决本题的关键．
29．已知△ABC内接于⊙O，∠BAC的平分线交⊙O于点D，连接DB，DC．
（1）如图①，当∠BAC＝120°时，请直接写出线段AB，AC，AD之间满足的等量关系式 AB+AC＝AD ；
（2）如图②，当∠BAC＝90°时，试探究线段AB，AC，AD之间满足的等量关系，并证明你的结论；
（3）如图③，若BC＝m，BD＝n，求的值（用含m，n的式子表示）．
【分析】（1）在AD上截取AE＝AB，连接BE，由条件可知△ABE和△BCD都是等边三角形，可证明△BED≌△BAC，可得DE＝AC，则AB+AC＝AD；
（2）延长AB至点M，使BM＝AC，连接DM，证明△MBD≌△ACD，可得MD＝AD，证得AB+ACAD；
（3）延长AB至点N，使BN＝AC，连接DN，证明△NBD≌△ACD，可得ND＝AD，∠N＝∠CAD，证△NAD∽△CBD，可得，可由AN＝AB+AC，求出的值．
【解答】解：（1）如图①在AD上截取AE＝AB，连接BE，
∵∠BAC＝120°，∠BAC的平分线交⊙O于点D，
∴∠DBC＝∠DAC＝60°，∠DCB＝∠BAD＝60°，
∴△ABE和△BCD都是等边三角形，
∴∠ABE＝∠DBC＝60°，
∴∠DBE＝∠ABC，
又∵AB＝BE，BC＝BD，
∴△BED≌△BAC（SAS），
∴DE＝AC，
∴AD＝AE+DE＝AB+AC；
故答案为：AB+AC＝AD．
（2）AB+ACAD．理由如下：
如图②，延长AB至点M，使BM＝AC，连接DM，
∵四边形ABDC内接于⊙O，
∴∠MBD＝∠ACD，
∵∠BAD＝∠CAD＝45°，
∴BD＝CD，
∴△MBD≌△ACD（SAS），
∴MD＝AD，∠M＝∠CAD＝45°，
∴MD⊥AD．
∴AMAD，即AB+BMAD，
∴AB+ACAD；
（3）如图③，延长AB至点N，使BN＝AC，连接DN，
∵四边形ABDC内接于⊙O，
∴∠NBD＝∠ACD，
∵∠BAD＝∠CAD，
∴BD＝CD，
∴△NBD≌△ACD（SAS），
∴ND＝AD，∠N＝∠CAD，
∴∠N＝∠NAD＝∠DBC＝∠DCB，
∴△NAD∽△CBD，
∴，
∴，
又AN＝AB+BN＝AB+AC，BC＝m，BD＝n，
∴．
【点评】本题属于圆的综合题，考查了圆周角定理，全等三角形的判定与性质，相似三角形的判定和性质，等边三角形的判定与性质等知识，解题的关键是正确作出辅助线解决问题．
30．如图，AB和CD为⊙O的直径，AB⊥CD，点E为CD上一点，CE＝CA，延长AE交⊙O于点F，连接CF交AB于点G．
（1）求证：CE2＝AE•AF；
（2）求证：∠ACF＝3∠BAF；
（3）若FG＝2，求AE的长．
【分析】（1）先判断出∠ACE＝∠AFC，进而判断出△ACE∽△AFC，得出AC2＝AE•AF，即可得出结论；
（2）先求出∠CAE＝∠CEA＝67.5°，进而求出∠BAF＝∠DCF＝22.5°，即可得出结论；
（3）先求出FH，GH，再判断出AH＝FH＝2，最后判断出EF＝FG，即可得出结论．
【解答】解：（1）∵AB和CD为⊙O的直径，AB⊥CD，
∴，
∴∠ACE＝∠AFC，
∵∠CAE＝∠FAC，
∴△ACE∽△AFC，
∴，
∴AC2＝AE•AF，
∵AC＝CE，
∴CE2＝AE•AF；
（2）∵AB⊥CD，
∴∠AOC＝90°，
∵OA＝OC，
∴∠ACE＝∠OAC＝45°，
∴∠AFC∠AOC＝45°，
∵AC＝CE，
∴∠CAE＝∠AEC（180°﹣∠ACO）＝67.5°，
∴∠BAF＝∠CAF﹣∠OAC＝22.5°，
∵∠AEC＝∠AFC+∠DAF＝45°+∠DCF＝67.5°，
∴∠DCF＝22.5°，
∴∠ACF＝∠OCA+∠DAF＝67.5°＝3×22.5°＝3∠BAF；
（3）如图，
过点G作GH⊥CF交AF于H，
∴∠FGH＝90°，
∵∠AFC＝45°，
∴∠FHG＝45°，
∴HG＝FG＝2，
∴FH＝2，
∵∠BAF＝22.5°，∠FHG＝45°，
∴∠AGH＝∠FHG﹣∠BAF＝22.5°＝∠BAF，
∴AH＝HG＝2，
∴AF＝AH+FH＝2+2，
由（2）知，∠OAE＝∠OCG，
∵∠AOE＝∠COG＝90°，OA＝OC，
∴△AOE≌△COG（SAS），
∴OE＝OG，∠AEO＝∠CGO，
∴∠OEF＝∠OGF，
连接EG，
∵OE＝OG，
∴∠OEG＝∠OGE＝45°，
∴∠FEG＝∠FGE，
∴EF＝FG＝2，
∴AE＝AF﹣EF＝2+22＝2．
【点评】此题是圆的综合题，主要考查了圆周角定理，全等三角形的判定和性质，相似三角形的判定和性质，等腰三角形的判定和性质，求出AF是解本题的关键．