专题13 向量线性运算及三大定理与四心归类（讲练）--2025年高考数学一轮复习高分冲刺

这是一份专题13 向量线性运算及三大定理与四心归类（讲练）--2025年高考数学一轮复习高分冲刺，文件包含专题13向量线性运算及三大定理与四心归类原卷版docx、专题13向量线性运算及三大定理与四心归类解析版docx等2份试卷配套教学资源，其中试卷共64页， 欢迎下载使用。
2、精练习题。不搞“题海战术”，在老师指导下，选一些源于课本的变式题，或体现基本概念、基本方法的基本题，通过解题来提高思维能力和解题技巧，加深对所学知识的深入理解。在解题时，要独立思考，一题多思，一题多解，反复玩味，悟出道理。
3、加强审题的规范性。每每大考过后，总有同学抱怨没考好，纠其原因是考试时没有注意审题。审题决定了成功与否，不解决这个问题势必影响到高考的成败。
4、重视错题。错误要及时寻找错因，及时进行总结，三五个字，一两句话都行，言简意赅，切中要害，以利于吸取教训，力求相同的错误不犯第二次。
专题13 向量线性运算及三大定理与四心归类
目录
\l "_Tc4571" 题型一：线性运算：等分点型
\l "_Tc9017" 题型二：线性运算：四边形等分点型
\l "_Tc25822" 题型三：线性运算：基底非同一起点
\l "_Tc16733" 题型四：三大定理：奔驰定理
\l "_Tc32648" 题型五：三大定理：极化恒等式
\l "_Tc25152" 题型六：三大定理：等和线基础
\l "_Tc23010" 题型七：等和线三角换元型
\l "_Tc27980" 题型八：等和线系数不是1构造型
\l "_Tc30478" 题型九：等和线均值型
\l "_Tc13560" 题型十：等和线二次型
\l "_Tc13338" 题型十一：等和线系数差型
\l "_Tc27842" 题型十二：四心向量：外心
\l "_Tc16015" 题型十三：四心向量：内心
\l "_Tc15373" 题型十四：四心向量：垂心
\l "_Tc30805" 题型十五：四心向量：重心
题型一：线性运算：等分点型
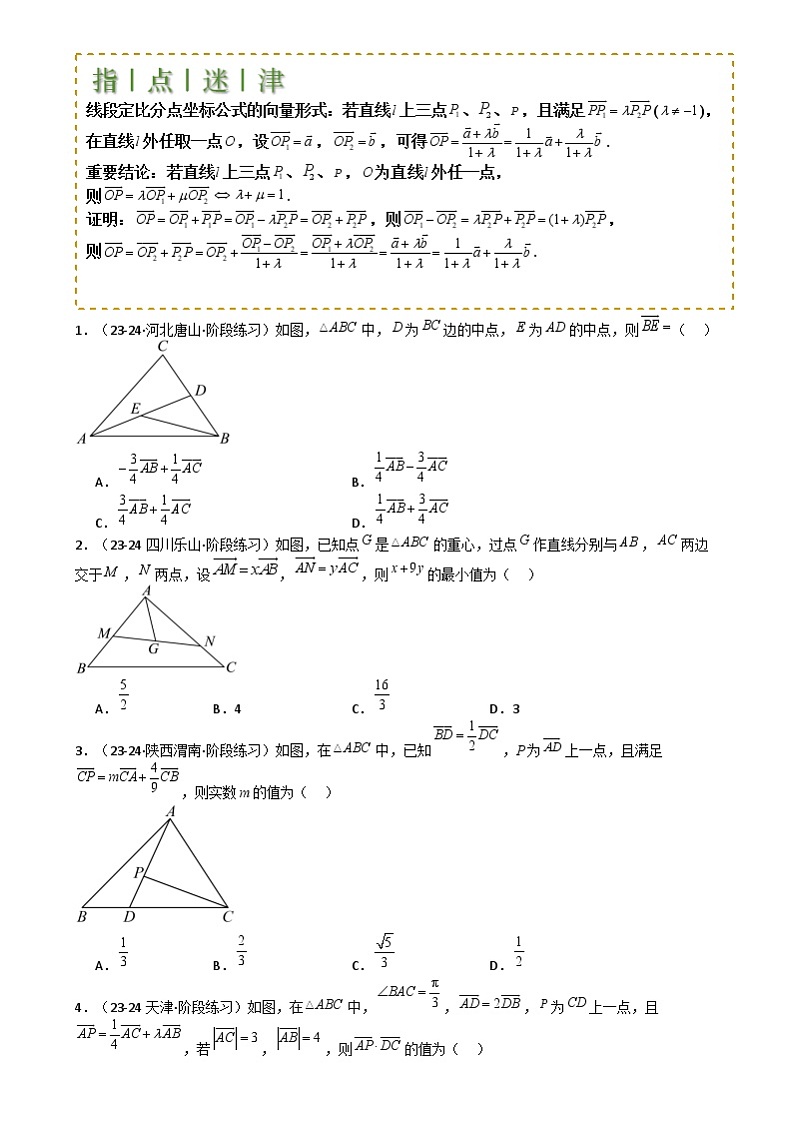
1．（23-24·河北唐山·阶段练习）如图，中，为边的中点，为的中点，则（ ）

A．B．
C．D．
2．（23-24四川乐山·阶段练习）如图，已知点是的重心，过点作直线分别与，两边交于，两点，设，，则的最小值为（ ）
A．B．4C．D．3
3．（23-24·陕西渭南·阶段练习）如图，在中，已知，P为上一点，且满足，则实数m的值为（ ）

A．B．C．D．
4．（23-24天津·阶段练习）如图，在中，，，为上一点，且，若，，则的值为（ ）

A．B．C．D．
5．（23-24甘肃临夏·阶段练习）如图，在中，点O是BC的中点，，分别连接MO、NO并延长，与边AB的延长线分别交于P，Q两点，若，则（ ）

A．2B．1C．－2D．－1
题型二：线性运算：四边形等分点型
1．（23-24·江苏苏州·阶段练习）在平行四边形中，，分别在边，上，，，与相交于点，记，，则（ ）
A．B．C．D．
2．（23-24山西·阶段练习）如图，在正方形中，,和相交于点G，且F为上一点（不包括端点），若，则的最小值为（ ）
A．B．C．D．15
3．（23-24宁夏银川·）如图所示的矩形中，，满足，，为的中点，若，则的值为（ ）
A．B．C．D．2
4．（23-24陕西咸阳）如图所示，在正方形中，为的中点，为的中点，若，则（ ）

A．B．C．D．
5．（23-24新疆乌鲁木齐·模拟）如图，在平行四边形中，，，与交于点.设，，若，则（ ）
A．B．C．D．
题型三：线性运算：基底非同一起点
1．（23-24·四川成都·）在正六边形ABCDEF中，，则（ ）
A．B．C．D．1
2．（23-24浙江·阶段练习）已知六边形ABCDEF为正六边形，且，，以下不正确的是（ ）

A．B．
C．D．
3．（23-24重庆巴南·阶段练习）如图，矩形中，点是线段上靠近的三等分点，点是线段的中点，则（ ）
A．B．
C．D．
4．（23-24高三河南·阶段练习）已知为等边三角形，分别以CA，CB为边作正六边形，如图所示，则（ ）
A．B．
C．D．
5．（22-23甘肃天水·阶段练习）如图，四边形是平行四边形，点分别为的中点，若以向量为基底表示向量，则下列结论正确的是（ ）

A．B．
C．D．
题型四：三大定理：奔驰定理
1．（23-24甘肃）“奔驰定理”因其几何表示酷似奔驰的标志得来，是平面向量中一个非常优美的结论.它的具体内容是：已知是内一点，，，的面积分别为，，，且.若为的垂心，，则（ ）

A．B．C．D．
2．（23-24河北）平面向量中有一个非常优美的结论：已知O为内的一点，，，的面积分别为，，，则．因其几何表示酷似奔驰的标志，所以称为“奔驰定理”．已知O为的内心，三个角对应的边分别为a，b，c，已知，，，则（ ）
A．B．C．D．
3．（2024上海·专题练习）“奔驰定理”因其几何表示酷似奔驰的标志得来，是平面向量中一个非常优美的结论．奔驰定理与三角形四心（重心、内心、外心、垂心）有着神秘的关联．它的具体内容是：已知是内一点，的面积分别为，且．以下命题错误的是（ ）
A．若，则为的重心
B．若为的内心，则
C．若，为的外心，则
D．若为的垂心，，则
4．（2023高三河南南阳·阶段练习）奔驰定理：已知是内的一点，，，的面积分别为，，，则．“奔驰定理”是平面向量中一个非常优美的结论，因为这个定理对应的图形与“奔驰”轿车（Mercedes benz）的lg很相似，故形象地称其为“奔驰定理”若是锐角内的一点，，，是的三个内角，且点满足，则必有（ ）
A．
B．
C．
D．
5．（2022·安徽·三模）平面上有及其内一点O，构成如图所示图形，若将，， 的面积分别记作，，，则有关系式．因图形和奔驰车的很相似，常把上述结论称为“奔驰定理”．已知的内角A，B，C的对边分别为a，b，c，若满足，则O为的（ ）
A．外心B．内心C．重心D．垂心
题型五：三大定理：极化恒等式
1.（2023·全国·统考高考真题）正方形的边长是2，是的中点，则（ ）
A．B．3C．D．5
2.（江苏·高考真题）如图，在中，是的中点，是上的两个三等分点，， ，则 的值是 .
3.如图,在中,已知,点分別在边上,
且,若为的中点,则的值为________
4.（23-24高三·湖南长沙·阶段练习）向量的数量积可以表示为：以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的四分之一，即如图所示，，我们称为极化恒等式. 已知在中，是中点，，，则（ ）
A．B．16C．D．8
5.（21-22·重庆沙坪坝·阶段练习）向量的数量积可以表示为：以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的四分之一.即如图所示：，我们称为极化恒等式.在△中，
是中点，，，则（ ）
A．32B．-32C．16D．-16
题型六：三大定理：等和线基础
1.（2023·江西吉安·高三统考阶段练习）如图，半径为的扇形的圆心角为120°，点C在弧上，且，若，则________.
2.（2023春·浙江温州·校考开学考试）两个单位向量且，点在弧上动，若，则的取值范围是___________________
3.正六边形中，令，，是△内含边界的动点（如图），，则的最大值是（ ）
A．1B．3C．4D．5
4.已知是的外心，，则，则的取值范围是
A．B．C．D．
5.已知在中，，，，P为BC上任意一点（含B，C），以P为圆心，1为半径作圆，Q为圆上任意一点，设，则的最大值为
A．B．C．D．
题型七：等和线三角换元型
1.（2023·全国·高一假期作业）如图，扇形的半径为1，且，点C在弧上运动，若，则的最大值是（ ）
A．B．C．1D．2
2.（2023春·湖北湖北省红安县第一中学校联考阶段练习）如图，扇形的半径为1，且，点C在弧上运动，若，则的最小值是（ ）
A．B．C．1D．2
3.（2023春·重庆万州·万州外国语学校天子湖校区校考阶段练习）如图，在半径为的圆中，点为圆上的定点，且，点为圆上的一个动点，若，则的取值范围是________．
4.在直角梯形.中，，分别为的中点，以为圆心，为半径的圆交于，点在上运动（如图）.若，其中，则的最大值是________.
5.已知正三角形的边长为2，D是边的中点，动点P满足，且，其中，则的最大值为___________．
题型八：等和线系数不是1构造型
1.如图，边长为2的等边三角形的外接圆为圆，为圆上任一点，若，则的最大值为（ ）
A．B．2C．D．1
2.（23-24·安徽芜湖·阶段练习）如图，已知点是的重心，过点作直线分别与，两边交于，两点，设，，则的最小值为（ ）

A．9B．4C．3D．
3.（2023·全国·高三专题练习）已知是内一点，且，点在内（不含边界），若，则的取值范围是
A．B．C．D．
4.（20-21·福建·阶段练习）已知平行四边形中，点E，F分别在边上，连接交于点M，且满足，则（ ）
A．B．1C．D．
题型九：等和线均值型
1.（2023春·四川眉山校考阶段练习）已知点G是的重心，过点G作直线分别与两边相交于点M，N两点（点M，N与点B，C不重合），设，，则的最小值为 ．
2.（2023春·重庆·校联考阶段练习）在中，点D满足，过点D的直线交线段AB于点M、交线段AC的延长线于点N，记，，则的最小值为 .
3.（2023春·山东菏泽统考模拟）在中，点是线段上的点，且满足，过点的直线分别交直线于点，且，，其中且，若的最小值为 .
4.（2023·全国·高三专题练习）已知A、B、P是直线上三个相异的点，平面内的点，若正实数x、y满足，则的最小值为 .
5.（23-24高三·天津武清·阶段练习）在中，，E是线段上的动点（与端点不重合），设，则的最小值是（ ）
A．10B．4C．7D．13
题型十：等和线二次型
1.（23-24·陕西西安·阶段练习）点是所在平面内一点，若，，则的最小值为（ ）
A．B．1C．D．
2.（2019秋·江苏苏州·校考阶段练习）如图，在正方形中，为的中点，是以为圆心，为半径的圆弧上的任意一点，设，则的最小值为 ．
3.（2024高三·全国·专题练习）已知的边的中点为，点在所在平面内，且，若，则（ ）
A．5B．10C．20D．30
4.（2022·全国·高三专题练习）已知为双曲线上不同三点，且满足（为坐标原点），直线的斜率记为，则的最小值为
A．8B．4C．2D．1
5.（2023·全国·高三专题练习）如图，在中，为边上不同于，的任意一点，点满足.若，则的最小值为 .

题型十一：等和线系数差型
1.（四川资阳·统考一模）如图，在直角梯形中，，∥，，，图中圆弧所在圆的圆心为点C，半径为，且点P在图中阴影部分（包括边界）运动．若，其中，则的最大值为
A．B．
C．2D．
2.（安徽合肥·统考一模）已知向量、、满足,若对于每一个确定的
的最大值和最小值分别为、 ，则对于任意的，的最小值为（ ）
A．B．C．D．
3.在中，点满足.若存在点，使得，且，则的取值范围是___．
4.（22-23高三·河北唐山·阶段练习）如图，在中，是线段上的一点，且，过点的直线分别交直线，于点，，若，，则的最小值是（ ）

A．B．C．D．
题型十二：四心向量：外心
1.（2023春·江苏无锡·锡东高中校考阶段练习）在中，，，，角是锐角，为的外心，若，其中，则点的轨迹所对应图形的面积是 ．
2.（2023春·广东佛山·南海中学校考阶段练习）如图，O为的外心，，，为钝角，是边的中点，则 .

3.（2023春·吉林长春·东北师大附中校考阶段练习）已知点O是△ABC的外心，AB＝4，AC＝2，∠BAC为钝角，M是边BC的中点，则 ．
4.（2023春·江西宜春·江西省清江中学校考阶段练习）设为的外心a，b，c分别为角A，B，C的对边，若，，则 ．
5.（2023春·辽宁·葫芦岛第一高级中学校联考阶段练习）已知为的外心，，，分别为内角，，的对边，且，则的取值范围是 .
题型十三：四心向量：内心
1.（2022春·甘肃兰州·兰州市第二中学校考模拟）在面上有及内一点满足关系式：即称为经典的“奔驰定理”，若的三边为，，，现有，则为的 心.
2.（2023浙江·模拟预测）已知中，，是的内心，是内部（不含边界）的动点，若，则的取值范围是（ ）
A．B．C．D．
3.（2022·贵州安顺·统考模拟预测）已知O是平面上的一个定点，A､B､C是平面上不共线的三点，动点P满足，则点P的轨迹一定经过的（ ）
A．重心B．外心C．内心D．垂心
4.（2023·全国·专题练习）已知所在的平面上的动点满足，则直线一定经过的（ ）
A．重心B．外心C．内心D．垂心
5.（2023春·全国·专题练习）已知，是其内心，内角所对的边分别，则（ ）
A．B．
C．D．
题型十四：四心向量：垂心
1.（2023·全国·高三专题练习）奔驰定理：已知是内的一点，若、、的面积分别记为、、，则．“奔驰定理”是平面向量中一个非常优美的结论，这个定理对应的图形与“奔驰”轿车的很相似，故形象地称其为“奔驰定理”.如图，已知是的垂心，且，则( )
A．B．C．D．
2.（2023春·浙江绍兴·校考阶段练习）奔驰定理：已知点O是内的一点，若的面积分别记为，则．“奔驰定理”是平面向量中一个非常优美的结论，因为这个定理对应的图形与“奔驰”轿车的lg很相似，故形象地称其为“奔驰定理”．如图，已知O是的垂心，且，则（ ）
A．B．C．D．
3.（2020·全国·高三专题练习）设是平面上一定点，A、B、C是平面上不共线的三点， 动点P满足，，则动点P的轨迹一定通过△ABC的
A．外心B．内心C．重心D．垂心
4.（2023·江苏·专题练习）已知点为所在平面内的动点，且满足，则点的轨迹一定通过的（ ）
A．垂心B．内心C．外心D．重心
5.（2020春·天津和平·耀华中学校考阶段练习）已知点O为△ABC所在平面内一点，且，则O一定为△ABC的（ ）
A．外心B．内心C．垂心D．重心
题型十五：四心向量：重心
1.（2023·全国·专题练习）在中，，，且，，则点的轨迹一定通过的（ ）
A．重心B．内心
C．外心D．垂心
2.（2023·全国·高三专题练习）已知的三个内角分别为为平面内任意一点，动点满足则动点P的轨迹一定经过的（ ）
A．重心B．垂心C．内心D．外心
3.（2021春·重庆渝中重庆复旦中学校考阶段练习）设是内任意一点，表示的面积，，，，定义.若是的重心，，则（ ）
A．点与点重合B．点在内
C．点在内D．点在内
4.（2022·全国·高三专题练习）设的内角的对边分别为，点为的重心且满足向量，若，则实数
A．3B．2C．D．