专题01 集合与常用逻辑用语（讲练）--2025年高考数学一轮复习基础夯实

这是一份专题01 集合与常用逻辑用语（讲练）--2025年高考数学一轮复习基础夯实，文件包含专题01集合与常用逻辑用语原卷版docx、专题01集合与常用逻辑用语解析版docx等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。
2、精练习题。不搞“题海战术”，在老师指导下，选一些源于课本的变式题，或体现基本概念、基本方法的基本题，通过解题来提高思维能力和解题技巧，加深对所学知识的深入理解。在解题时，要独立思考，一题多思，一题多解，反复玩味，悟出道理。
3、加强审题的规范性。每每大考过后，总有同学抱怨没考好，纠其原因是考试时没有注意审题。审题决定了成功与否，不解决这个问题势必影响到高考的成败。
4、重视错题。错误要及时寻找错因，及时进行总结，三五个字，一两句话都行，言简意赅，切中要害，以利于吸取教训，力求相同的错误不犯第二次。
专题01 集合与常用逻辑用语
（思维构建+知识盘点+重点突破+方法技巧+易混易错）
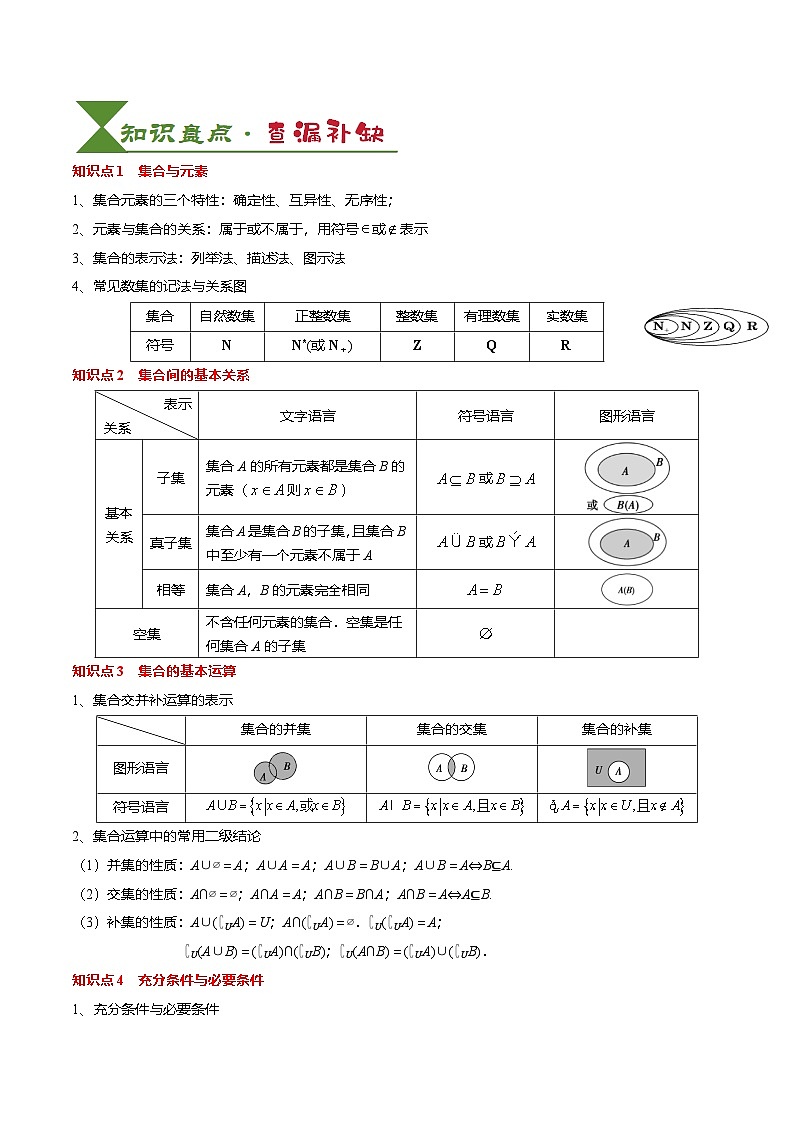
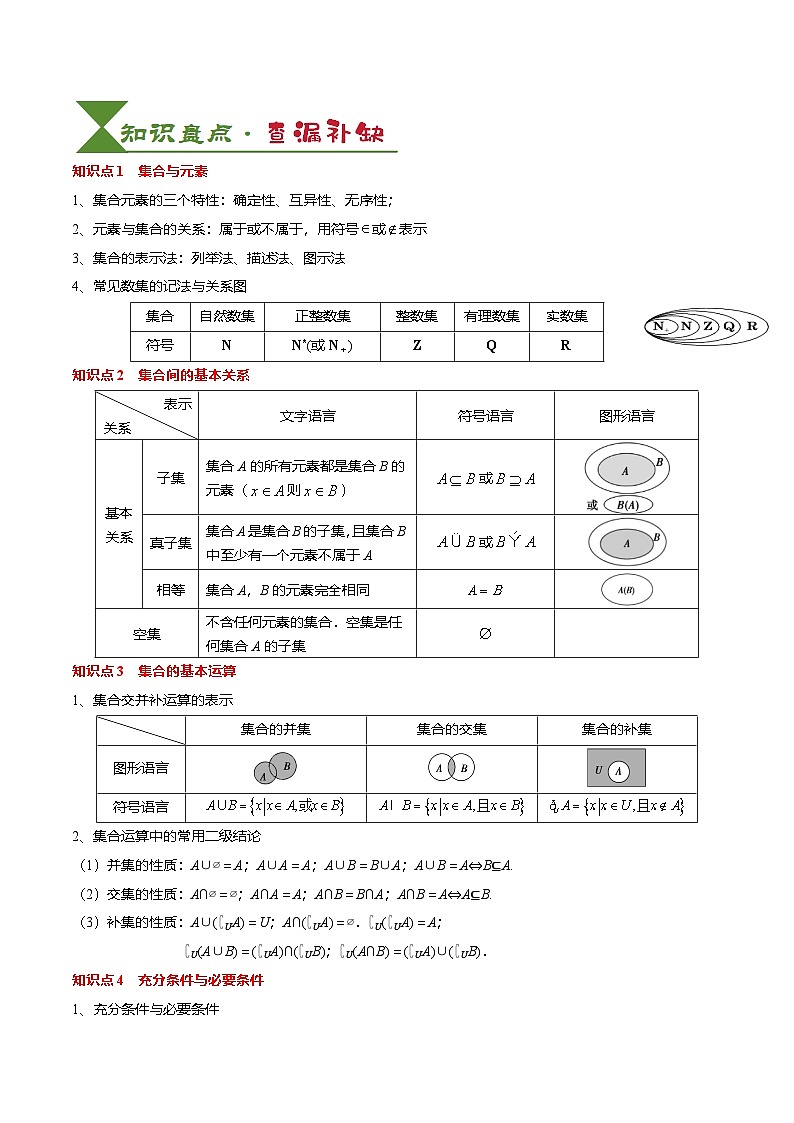
知识点1 集合与元素
1、集合元素的三个特性：确定性、互异性、无序性；
2、元素与集合的关系：属于或不属于，用符号或表示
3、集合的表示法：列举法、描述法、图示法
4、常见数集的记法与关系图
知识点2 集合间的基本关系
知识点3 集合的基本运算
1、集合交并补运算的表示
2、集合运算中的常用二级结论
（1）并集的性质：A∪∅＝A；A∪A＝A；A∪B＝B∪A；A∪B＝A⇔B⊆A.
（2）交集的性质：A∩∅＝∅；A∩A＝A；A∩B＝B∩A；A∩B＝A⇔A⊆B.
（3）补集的性质：A∪(∁UA)＝U；A∩(∁UA)＝∅．∁U(∁UA)＝A；
∁U(A∪B)＝(∁UA)∩(∁UB)；∁U(A∩B)＝(∁UA)∪(∁UB)．
知识点4 充分条件与必要条件
1、充分条件与必要条件
2、充要条件
（1）充要条件的定义
如果“若，则”和它的逆命题“若，则”均为真命题，即既有，又有，就记作。
此时，既是的充分条件，也是的必要条件，我们说是的充分必要条件，简称充要条件。
（2）充要条件的含义
若是的充要条件，则也是的充要条件，虽然本质上是一样的，但在说法上还是不同的，
因为这两个命题的条件与结论不同。
（3）充要条件的等价说法：是的充要条件又常说成是成立当且仅当成立，或与等价。
知识点5 全称量词与存在量词
1、全称量词与全称量词命题
（1）全称量词：短语“所有的”“任意一个”在逻辑中通常叫作全称量词，并用符号“”表示．
【注意】（1）全称量词的数量可能是有限的，也可能是无限的，由有题目而定；
（2）常见的全称量词还有“一切”、“任给”等，相应的词语是“都”
（2）全称量词命题：含有全称量词的命题，称为全称量词命题．
符号表示：通常，将含有变量的语句用，，，…表示，变量的取值范围用表示，那么，全称量词命题“对中任意一个，成立”可用符号简记为
【注意】（1）从集合的观点看，全称量词命题是陈述某集合中所有元素都具有某种性质的命题；
（2）一个全称量词命题可以包含多个变量；
（3）有些全称量词命题中的全称量词是省略的，理解时需要把它补出来。
如：命题“平行四边形对角线互相平行”理解为“所有平行四边形对角线都互相平行”。
2、存在量词与存在量词命题
（1）存在量词：短语“存在一个”“至少有一个”在逻辑中通常叫作存在量词，并用符号“”表示．
【注意】常见的存在量词还有“有些”、“有一个”、“对某些”、“有的”等；
（2）存在量词命题：含有存在量词的命题，叫作存在量词命题。
符号表示：存在量词命题“存在中的元素，使成立”可用符号简记为
【注意】（1）从集合的观点看，存在量词命题是陈述某集合中有一些元素具有某种性质的命题；
（2）一个存在量词命题可以包含多个变量；
（3）有些命题虽然没有写出存在量词，但其意义具备“存在”、“有一个”等特征都是存在量词命题
3、命题的否定：对命题p加以否定，得到一个新的命题，记作“”，读作“非p”或p的否定．
（1）全称量词命题的否定：
一般地，全称量词命题“”的否定是存在量词命题： ．
（2）存在量词命题的否定：
一般地，存在量词命题“ ”的否定是全称量词命题： ．
（3）命题与命题的否定的真假判断：
一个命题和它的否定不能同时为真命题，也不能同时为假命题，只能一真一假．
即：如果一个命题是真命题，那么这个命题的否定是假命题，反之亦然．
（4）常见正面词语的否定：
重难点01 已知一个元素属于集合，求集合中所含的参数值．
（1）确定性的运用：利用集合中元素的确定性解出参数的所有可能值；
（2）互异性的运用：根据集合中元素的互异性对集合中元素进行检验．
【典例1】（23-24高三上·广东惠州·月考）集合 ，若且，则的取值范围为（ ）
A．B．C．D．
【答案】B
【解析】因为且，所以且，解得.故选：B.
【典例2】（23-24高三下·江西·月考）已知，若，且，则的取值范围是（ ）
A．B．C．D．
【答案】A
【解析】由题意得且，解得．故选：A
重难点02 利用两个集合之间的关系确定参数的取值范围
第一步：弄清两个集合之间的关系，谁是谁的子集；
第二步：看集合中是否含有参数，若，
且A中含参数应考虑参数使该集合为空集的情形；
第三步：将集合间的包含关系转化为方程(组)或不等式(组)，求出相关的参数的值或取值范围.
常采用数形结合的思想，借助数轴解答.
【典例1】（2024·陕西西安·三模）设集合，，若，则（ ）
A．2B．3C．1D．1或2
【答案】C
【解析】因为，且，
所以，则或，解得或，
当时，不满足集合元素的互异性，故舍去；
当时，符合题意.
综上可得.故选：C
【典例2】（2024·黑龙江·二模）已知，若，则实数的取值范围为（ ）
A．B．C．D．
【答案】A
【解析】因为，，
又，所以，故.故选：A.
重难点03 根据集合运算的结果确定参数的取值范围
法一：根据集合运算结果确定集合对应区间的端点值之间的大小关系，确定参数的取值范围.
法二：（1）化简所给集合；（2）用数轴表示所给集合；
（3）根据集合端点间关系列出不等式（组）；（4）解不等式（组）；（5）检验.
【注意】（1）确定不等式解集的端点之间的大小关系时，需检验能否取“=”；（2）千万不要忘记考虑空集。
【典例1】（2024·重庆·模拟预测）设集合，，若， 则（ ）
A．1B．C．2D．
【答案】B
【解析】当时，，则，
即此时，，不符合要求；
当时，，则，
即此时，，符合要求；
故.故选：B.
【典例2】（2024·重庆·模拟预测）已知集合，，若，则a的取值范围为（ ）
A．B．C．D．
【答案】A
【解析】由不等式，解得或，所以或，
又由不等式，
当时，不等式解集为空集，不满足，不符合题意，舍去；
当时，解得，即，
此时不满足，不符合题意，舍去；
当时，解得，即，
要使得，则满足，
综上可得，实数的取值范围为.故选：A.
重难点 04 利用充分必要条件求参数的策略
1、巧用转化法求参数：把充分条件、必要条件转化为集合之间的关系，然后根据集合之间的关系列出关于参数的不等式（不等式组）求解；
2、端点取值需谨慎：在求参数范围时，要注意边界或区间端点值的检验，从而确定取舍。
【典例1】（23-24高三上·上海松江·期中）已知，且是的充分不必要条件，则实数的取值范围是 .
【答案】
【解析】，解得，设，，
若是的充分不必要条件，则，
则有，且等号不会同时取到，解得，
则实数的取值范围是.
【典例2】（23-24高三上·江苏扬州·月考）（多选）若“”是“”的必要不充分条件，则实数可以是（ ）
A．B．C．D．
【答案】AD
【解析】由不等式，可得或，
因为是的必要不充分条件，可得或，
解得或，即实数的取值范围为，
结合选项，可得A、D符合题意.故选：AD.
重难点 05 根据全称（存在）量词命题的真假求参数
1、全称量词命题求参的问题，常以一次函数、二次函数等为载体进行考察，一般在题目中会出现“恒成立”等词语，解决此类问题时，可构造函数，利用数形结合求参数范围，也可用分离参数法求参数范围；
2、存在量词命题求参数范围的问题中常出现“存在”等词语，对于此类问题，通常时假设存在满足条件的参数，然后利用条件求参数范围，若能求出参数范围，则假设成立；否则，假设不成立。解决有关存在量词命题的参数的取值范围问题时，应尽量分离参数。
【典例1】（2024·四川·模拟预测）已知命题“”为真命题，则实数的取值范围为（ ）
A．B．C．D．
【答案】A
【解析】因为命题“”为真命题，所以．
令与在上均为增函数，
故为增函数，当时，有最小值，即，故选：A．
【典例2】（23-24高三上·黑龙江哈尔滨·期末）已知命题：为假命题，则实数的取值范围是（ ）
A．B．C．D．
【答案】D
【解析】由题意知命题：为假命题，
则命题：为真命题，
故当时，，即为，符合题意；
当时，需满足，解得，
综合可得实数的取值范围是，故选：D
一、子集的个数问题
如果集合A中含有n个元素，则有
（1）A的子集的个数有2n个． （2）A的非空子集的个数有2n－1个．
（3）A的真子集的个数有2n－1个 （4）A的非空真子集的个数有2n－2个．
【典例1】（2024·浙江·二模）已知集合，，若，则满足集合的个数为（ ）
A．4B．6C．7D．8
【答案】D
【解析】因为，
所以可以是，
共8个，故选：D
【典例2】（2024·全国·一模）已知集合，，则子集的个数为（ ）
A．1B．2C．3D．4
【答案】D
【解析】由，得，解得，
所以，所以，
所以子集的个数为.故选：D
二、判断集合与集合的关系
判断集合间关系的常用方法：
1、列举观察法：列出几何中的全部元素，通过定义得出集合间关系；
2、集合元素特征法：首先确定集合的代表元素是什么，弄清楚集合元素的特征，再利用集合元素的特征判断集合间关系；
3、数形结合法：利用数轴或韦恩图判断集合间关系，如不等式的解集之间的关系，适合用数轴法。
【典例1】（2024·云南贵州·二模）已知集合，，则（ ）
A．B．C．D．
【答案】A
【解析】由题意可得，所以.故选：A
【典例2】（2024高三·全国·专题练习）已知集合，，则下列关系中正确的是（ ）
A．B．C．D．
【答案】D
【解析】由题意知，，解得或，
则，，
则不是B的子集，不是的子集，，，故选：D．
三、韦恩图的应用
元素与集合的隶属关系以及集合之间的包含关系，一般都能通过韦恩图形象表达。有时题设条件比较抽象，也应借助于韦恩图寻找解题思路。这样做有助于直观地分析问题、解决问题。
【典例1】（2024·山西长治·一模）已知集合，则图中阴影部分表示的集合为（ ）
A．B．C．D．
【答案】A
【解析】因为，
图中阴影部分表示的集合为：或，
故选：A.
【典例2】（2024·河北邢台·二模）下列集合关系不成立的是（ ）
A．B．
C．D．
【答案】D
【解析】A：因为，故A正确；
B：由空集的定义可知，故B正确；
C：由图可知C正确；
D：因为空集中不包含任何元素，故D错误；故选：D.
四、集合新定义问题
在集合新定义问题中，出现较多的是在现有运算法则和运算律的基础上定义一种新的运算。解题时，要抓住两点：（1）分析新定义的特点，把新定义中所叙述的问题的本质弄清楚，并且能够应用到具体的解题过程中；（2）集合中元素的特性及集合的基本运算是解题的突破口，要熟练掌握。
【典例1】（2024·贵州黔东南·二模）若对任意，，则称A为“影子关系”集合，下列集合为“影子关系”集合的是（ ）
A．B．C．D．
【答案】D
【解析】对于选项A：因为，但，不符合题意，故A错误；
对于选项B：因为，但无意义，不符合题意，故B错误；
对于选项C：例如，但，不符合题意，故C错误，
对于选项D：对任意，均有，符合题意，故D正确；故选：D.
【典例2】（23-24高三下·甘肃·月考）如果集合U存在一组两两不交（两个集合交集为空集时，称为不交）的非空子集，且满足，那么称子集组构成集合U的一个k划分．若集合I中含有4个元素，则集合I的所有划分的个数为（ ）
A．7个B．9个C．10个D．14个
【答案】D
【解析】不妨设，则：
的2划分有，，，
，，，；
的3划分有，，，
，，；
的4划分只有.
综上，的划分共有个，D正确.故选：D.
五、充分条件与必要条件的判断
充分条件、必要条件、充要条件的判断方法
1、定义法：（1）分清命题的条件和结论；（2）判断“若p，则q”及“若q，则p”的真假；（3）得出结论.
2、集合法：利用集合间的包含关系进行判断；
3、等价转化法：将命题转化为另一个与之等价的且便于判断真假的命题。
【典例1】（2024·江西南昌·二模）已知集合，则“”是“”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
【答案】A
【解析】不等式解得，则；
不等式解得，则.
，所以“”是“”的充分不必要条件.故选：A
【典例2】（2024·湖南衡阳·模拟预测）已知命题p：集合，命题q：集合，则p是q的（ ）条件
A．充分不必要B．必要不充分C．充分必要D．既不充分也不必要
【答案】B
【解析】或，或，
是的真子集，
因此，是的必要不充分条件.故选：B

易错点1 对集合表示方法的理解存在偏差
点拨：对集合表示法的理解不能只流于形式上的“掌握”，要对本质进行剖析，需要明确集合中的代表元素类型（点集或者数集）及代表元素的含义。
【典例1】（23-24高三下·江西吉安·期中）已知集合，，则（ ）
A．B．C．D．
【答案】D
【解析】解不等式可得，
由指数函数的值域可得，所以.故选：D
【典例2】（2024·湖北·模拟预测）已知集合，，则（ ）
A．B．C．D．
【答案】B
【解析】由，
当且仅当，即时，等号成立，得；
由得，即.所以.故选：B
易错点2 忽视（漏）空集导致错误
点拨：空集不含任何元素，在解题过程中容易被忽略，特别是在隐含有空集参与的集合问题中，往往容易因忽略空集的特殊性而导致漏解。
【典例1】（2024·重庆·模拟预测）设若，，则，实数的取值集合为（ ）
A．B．C．D．
【答案】D
【解析】由题，得，
因为，所以，
当时，无解，此时，满足题意；
当时，得，所以或，解得或.
综上，实数a的值可以为0，，.故选：D．
【典例2】（2024·全国·模拟预测）已知全集，集合，．若，则的最大值为 ．
【答案】
【解析】因为，
当时，，若，则．
在数轴上表示出集合，，如图，
则；
当时，，此时不成立，
当时，，此时不成立．
综上，的最大值为．
易错点3 忽视集合元素的互异性
点拨：集合元素的互异性是集合的特征之一，集合中不可出现相同的元素。
【典例1】（2024·内蒙古呼伦贝尔·二模）已知集合，，若中恰有三个元素，则由a的取值组成的集合为（ ）
A．B．C．D．
【答案】D
【解析】因为中恰有三个元素，所以或或，
结合集合中元素的互异性，解得或或（舍去）或.故选：D．
【典例2】（2024高三·全国·专题练习）已知集合，且，则实数为（ ）
A．2B．3C．0或3D．
【答案】B
【解析】因为且，所以或，
①若，此时，不满足元素的互异性；
②若，解得或3，
当时不满足元素的互异性，当时，符合题意.
综上所述，.故选：B
易错点4 判断充分性必要性位置颠倒
点拨：需要多注意倒装句的标志，解题时先翻译成正常的结构再判断计算。
【典例1】（2024·新疆·二模）使“”成立的一个充分不必要条件是（ ）
A．B．C．D．
【答案】B
【解析】由，得，解得，则选项中的的范围组成的集合是的真子集，
由选项知，选项均不满足，选项B满足.
故使“”成立的一个充分不必要条件可以是“”.故选：B.
【典例2】（23-24高三上·天津南开·月考）若x，，则“”的一个必要不充分条件可以是（ ）
A．B．C．D．
【答案】A
【解析】A：，是“”的必要不充分条件，故A正确；
B：，是“”的既不充分也不必要条件，故B错误；
C：，是“”的既不充分也不必要条件，故C错误；
D：，是“”的充分不必要条件，故D错误；故选：A
易错点5 对含有一个量词命题的否定理解错误
点拨：对含有一个量词的命题进行否定时，除了将存在量词命题变为全称量词命题，全称量词命题变为存在量词命题外，不等式的否定只否定结论。
【典例1】（2024·贵州遵义·一模）已知命题，，则为（ ）
A．，B．，
C．，D．，
【答案】D
【解析】由命题，可知，
为，，故D正确；ABC错误；故选：D
【典例2】（23-24高三下·山东菏泽·开学考试）命题“，”的否定为（ ）
A．，B．，
C．，D．，
【答案】D
【解析】因为全称量词命题的否定是存在量词命题，
故命题“，”的否定为，.故选：D.集合
自然数集
正整数集
整数集
有理数集
实数集
符号
N
N*(或N＋)
Z
Q
R
表示
关系
文字语言
符号语言
图形语言
基本关系
子集
集合A的所有元素都是集合B的元素（则）
或
真子集
集合A是集合B的子集，且集合B中至少有一个元素不属于A
或
相等
集合A，B的元素完全相同
空集
不含任何元素的集合．空集是任何集合A的子集
集合的并集
集合的交集
集合的补集
图形语言
符号语言
“若p，则q”为真命题
“若p，则q”为假命题
推出关系
p⇒q
p⇏q
条件关系
p是q的充分条件
q是p的必要条件
p不是q的充分条件
q不是p的必要条件
定理关系
判定定理给出了相应数学结论成立的充分条件
性质定理给出了相应数学结论成立的必要条件
正面词语
等于（＝）
大于（＞）
小于（＜）
是
都是
否定
不等式（≠）
不大于（≤）
不小于（≥）
不是
不都是
正面词语
至多有一个
至少有一个
任意
所有
至多有n个
否定
至少有两个
一个都没有
某个
某些
至少有n+1个