2025高考数学一轮复习-7.4-空间直线、平面的平行-专项训练【含答案】

这是一份2025高考数学一轮复习-7.4-空间直线、平面的平行-专项训练【含答案】，共9页。
1．下列命题中正确的是( )
A．若a，b是两条直线，且a∥b，那么a平行于经过b的任何平面
B．若直线a和平面α满足a∥α，那么a与α内的任何直线平行
C．平行于同一条直线的两个平面平行
D．若直线a，b和平面α满足a∥b，a∥α，b⊄α，则b∥α
2．已知P为△ABC所在平面外一点，平面α∥平面ABC，且α交线段PA，PB，PC于点A′，B′，C′.若PA′∶AA′＝2∶3，则S△A′B′C′∶S△ABC等于( )
A．2∶3 B．2∶5
C．4∶9 D．4∶25
3．(多选)如图，在空间四边形ABCD中，E，F分别为AB，AD的中点，G，H分别在BC，CD上，且BG∶GC＝DH∶HC＝1∶2，则下列结论正确的是( )
A．BD∥平面EGHF
B．FH∥平面ABC
C．AC∥平面EGHF
D．直线GE，HF，AC交于一点
4．如图，在正方体ABCD­A1B1C1D1中，AB＝2，点E为AD的中点，点F在CD上．若EF∥平面AB1C，则线段EF的长等于________．
5．如图，在直三棱柱ABC­A1B1C1中，点D，E，F分别为AB，A1B1，BC的中点，线段CD与线段AF交于点G.
(1)求证：平面AC1E∥平面B1CD；
(2)若AC＝BC＝CC1＝2，AC⊥BC，求三棱锥A­A1C1G的体积．
INCLUDEPICTURE "B组.TIF" INCLUDEPICTURE "E:\\大样\\人教数学\\B组.TIF" \* MERGEFORMATINET 【B级 能力提升】
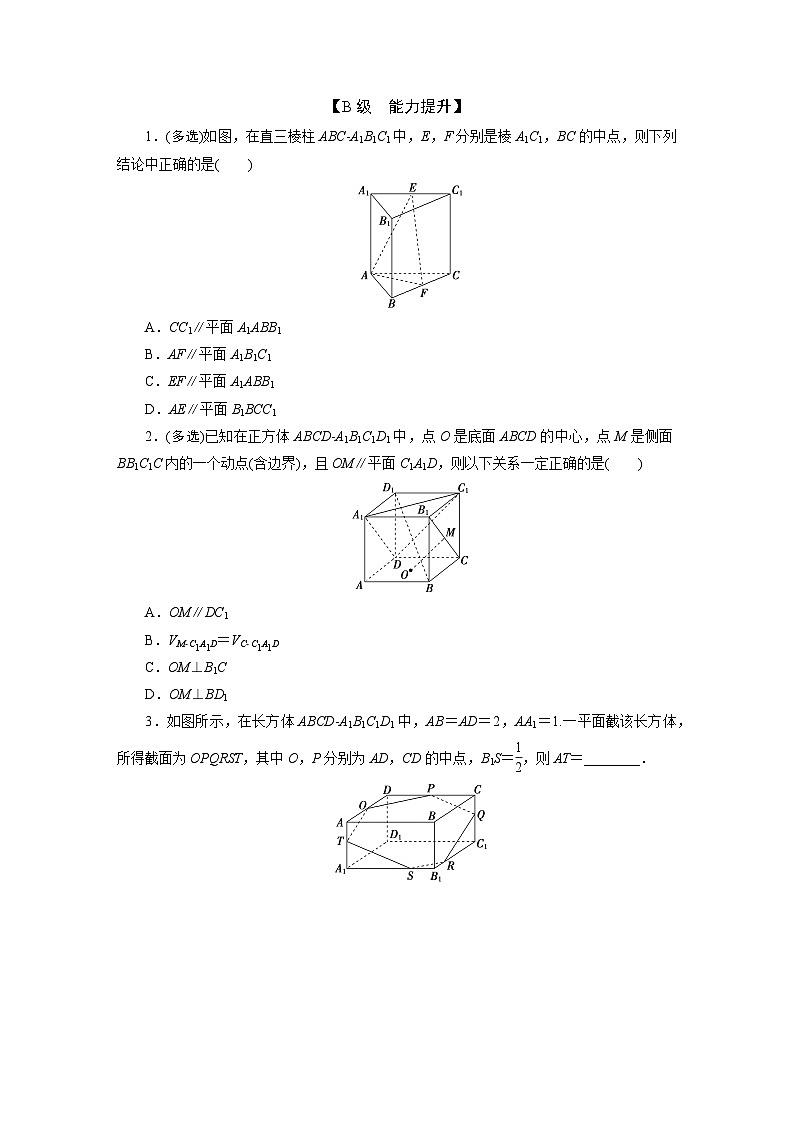
1．(多选)如图，在直三棱柱ABC­A1B1C1中，E，F分别是棱A1C1，BC的中点，则下列结论中正确的是( )
A．CC1∥平面A1ABB1
B．AF∥平面A1B1C1
C．EF∥平面A1ABB1
D．AE∥平面B1BCC1
2．(多选)已知在正方体ABCD­A1B1C1D1中，点O是底面ABCD的中心，点M是侧面BB1C1C内的一个动点(含边界)，且OM∥平面C1A1D，则以下关系一定正确的是( )
A．OM∥DC1
B．VM­C1A1D＝VC­C1A1D
C．OM⊥B1C
D．OM⊥BD1
3．如图所示，在长方体ABCD­A1B1C1D1中，AB＝AD＝2，AA1＝1.一平面截该长方体，所得截面为OPQRST，其中O，P分别为AD，CD的中点，B1S＝ eq \f(1,2)，则AT＝________．
4．如图，在多面体ABCDEF中，四边形ABCD是正方形，BF⊥平面ABCD，DE⊥平面ABCD，BF＝DE，M为棱AE的中点．
(1)求证：平面BDM∥平面EFC；
(2)若AB＝1，BF＝2，求三棱锥A­CEF的体积．
参考答案
【A级 基础巩固】
1．解析：A中，a可以在过b的平面内；B中，a与α内的直线也可能异面；C中，两平面可相交；D中，由直线与平面平行的判定定理知b∥α，故D正确．
答案：D
2．解析：∵平面α∥平面ABC，
∴A′C′∥AC，A′B′∥AB，B′C′∥BC，
∴S△A′B′C′∶S△ABC＝(PA′∶PA)2.
又PA′∶AA′＝2∶3，
∴PA′∶PA＝2∶5，
∴S△A′B′C′∶S△ABC＝4∶25.
答案：D
3．解析：因为BG∶GC＝DH∶HC，
所以GH∥BD.
又E，F分别为AB，AD的中点，
所以EF∥BD，且EF＝ eq \f(1,2)BD，
则EF∥GH.
易知BD∥平面EGHF，FH与AC为相交直线，
故A正确，B，C错误；
因为EF∥GH，且EF≠GH，
所以四边形EGHF为梯形，
所以EG与FH必相交，设交点为M，
而EG⊂平面ABC，FH⊂平面ACD，
则点M在平面ABC与平面ACD的交线上．
又平面ABC∩平面ACD＝AC，
所以M∈AC，即直线GE，HF，AC交于一点，
故D正确．
答案：AD
4．解析：因为EF∥平面AB1C，EF⊂平面ABCD，平面ABCD∩平面AB1C＝AC，
所以EF∥AC，所以点F为DC的中点，
故EF＝ eq \f(1,2)AC＝ eq \r(2).
答案： eq \r(2)
5．(1)证明：如图，连接ED.因为在三棱柱ABC­A1B1C1中，D，E分别为AB，A1B1的中点，
所以DE∥CC1，
且DE＝CC1，
则四边形DEC1C是平行四边形，
故EC1∥DC.
又CD⊂平面B1CD，EC1⊄平面B1CD，
所以EC1∥平面B1CD.
因为在三棱柱ABC­A1B1C1中，D，E分别为AB，A1B1的中点，
所以B1E∥AD，且B1E＝AD，
所以四边形B1EAD是平行四边形，
所以EA∥DB1.
又DB1⊂平面B1CD，EA⊄平面B1CD，
所以EA∥平面B1CD.
又EA⊂平面AC1E，EC1⊂平面AC1E，
且EA∩EC1＝E，
所以平面AC1E∥平面B1CD.
(2)解：因为AC＝BC＝CC1＝2，AC⊥BC，
所以S△A1C1A＝ eq \f(1,2)AA1·A1C1＝ eq \f(1,2)×2×2＝2，过点G作GH⊥AC于点H，
连接DF.由题意可知AA1⊥平面ABC，GH⊂平面ABC，所以AA1⊥GH.
又AA1∩AC＝A，AA1，AC⊂平面ACC1A1，
所以GH⊥平面ACC1A1.
因为D，F分别是AB，BC的中点，
所以DF＝ eq \f(1,2)AC，且DF∥AC，
所以 eq \f(DG,GC)＝ eq \f(DF,AC)＝ eq \f(1,2)，
其中CD＝ eq \f(1,2)AB＝ eq \r(2)，
所以CG＝ eq \f(2\r(2),3)，
易知△CGH是等腰直角三角形．
所以GH＝ eq \f(2,3)，VA­A1C1G＝VG­A1C1A
＝ eq \f(1,3)S△A1AC1·GH＝ eq \f(4,9)，
故三棱锥A­A1C1G的体积为 eq \f(4,9).
INCLUDEPICTURE "B组.TIF" INCLUDEPICTURE "E:\\大样\\人教数学\\B组.TIF" \* MERGEFORMATINET 【B级 能力提升】
1．解析：在直三棱柱ABC­A1B1C1中，因为CC1∥AA1，CC1⊄平面A1ABB1，AA1⊂平面A1ABB1，所以CC1∥平面A1ABB1，A正确；
因为平面ABC∥平面A1B1C1，AF⊂平面ABC，所以AF∥平面A1B1C1，B正确；
取AB的中点G，连接A1G，GF(图略)，
因为G，F分别是棱AB，BC的中点，
所以GF綉 eq \f(1,2)AC，且A1E綉 eq \f(1,2)AC，
所以GF綉A1E，所以四边形GFEA1为平行四边形，
所以EF∥A1G，EF⊄平面A1ABB1，A1G⊂平面A1ABB1，
所以EF∥平面A1ABB1，C正确；
取AC的中点H，连接C1H(图略)，易证得四边形AHC1E为平行四边形，所以EA∥C1H，C1H与平面B1BCC1相交，所以AE与平面B1BCC1相交，D不正确．
答案：ABC
2．解析：对于A，如图，连接AB1，AC，
由正方体的性质可得平面A1C1D∥平面AB1C.
因为OM∥平面C1A1D，且点M是侧面BB1C1C内的一个动点，
所以点M在线段B1C上，
所以OM与DC1不一定平行，故A错误；
对于B，由选项A知B1C∥平面C1A1D，由线面平行的性质可知点C与点M到平面C1A1D的距离相等，故VM­C1A1D＝VC­C1A1D，故B正确；
对于C，因为点O为AC的中点，点M在线段B1C上，所以OM与B1C不一定垂直，故C错误；
对于D，根据正方体性质易知BD1⊥平面AB1C，OM⊂平面AB1C，所以OM⊥BD1，故D正确．
答案：BD
3．解析：设AT＝x，则A1T＝1－x，
由面面平行的性质可知PO∥SR，TO∥QR，TS∥PQ，
∴△DOP∽△B1RS.
∵DP＝OD＝1，∴B1S＝B1R＝ eq \f(1,2)，
∴A1S＝C1R＝ eq \f(3,2).
由△ATO∽△C1QR，可得 eq \f(AO,AT)＝ eq \f(C1R,C1Q)，
即 eq \f(1,x)＝ eq \f(\f(3,2),C1Q)，故C1Q＝ eq \f(3x,2).
由△A1TS∽△CQP，可得 eq \f(CQ,CP)＝ eq \f(A1T,A1S)，
即 eq \f(1－\f(3x,2),1)＝ eq \f(1－x,\f(3,2))，解得x＝ eq \f(2,5).
答案： eq \f(2,5)
4．(1)证明：如图，设AC与BD交于点N，
则N为AC的中点，连接MN.
又M为棱AE的中点，∴MN∥EC.
∵MN⊄平面EFC，EC⊂平面EFC，
∴MN∥平面EFC.
∵BF⊥平面ABCD，DE⊥平面ABCD，∴BF∥DE，且BF＝DE，
∴四边形BDEF为平行四边形，∴BD∥EF.
∵BD⊄平面EFC，EF⊂平面EFC，∴BD∥平面EFC.
又MN∩BD＝N，MN，BD⊂平面BDM，
∴平面BDM∥平面EFC.
(2)解：连接EN，FN.
在正方形ABCD中，AC⊥BD.
又BF⊥平面ABCD，∴BF⊥AC.
又BF∩BD＝B，BF，BD⊂平面BDEF，
∴AC⊥平面BDEF.又N是AC的中点，
∴V三棱锥A­NEF＝V三棱锥C­NEF，
∴V三棱锥A­CEF＝2V三棱锥A­NEF＝2× eq \f(1,3)×AN×S△NEF＝2× eq \f(1,3)× eq \f(\r(2),2)× eq \f(1,2)× eq \r(2)×2＝ eq \f(2,3)，
∴三棱锥A­CEF的体积为 eq \f(2,3)