艺考生教学课件29空间直线、平面的垂直-2024-2025学年高考数学艺体生一轮复习课件

这是一份艺考生教学课件29空间直线、平面的垂直-2024-2025学年高考数学艺体生一轮复习课件，共60页。PPT课件主要包含了线线角，线面角，二面角，教材知识萃取，教材素材变式，任意一条，规律总结，半平面，直二面角，方法技巧等内容，欢迎下载使用。
直线与平面垂直的判定与性质
平面与平面垂直的判定与性质
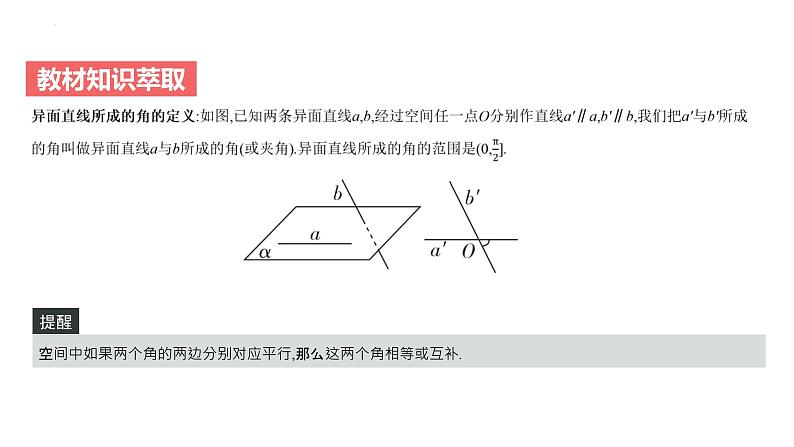
空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.
方法技巧求异面直线所成角的步骤（1）构造：根据异面直线的定义，用平移法（常利用三角形中位线、平行四边形的性质）作出异面直线所成的角.（2）证明：证明作出的角就是要求的角.（3）计算：求角度（常利用三角形的有关知识）.（4）结论：若求出的角是锐角或直角，则它就是所求异面直线所成的角；若求出的角是钝角，则它的补角就是所求异面直线所成的角.
（2）直线与平面垂直的判定定理和性质定理
平行
垂直关系中常用的6个结论
（1）若一条直线垂直于一个平面，则它垂直于这个平面内的任何一条直线（证明线线垂直的一个重要方法）．
（2）若两条平行线中的一条直线垂直于一个平面，则另一条直线也垂直于这个平面．
（3）若一条直线垂直于两平行平面中的一个平面，则这条直线与另一个平面也垂直.
（4）两个相交平面同时垂直于第三个平面，它们的交线也垂直于第三个平面．
（5）三垂线定理：平面内的一条直线，如果它和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直.
（6）三垂线定理的逆定理：平面内的一条直线，如果它和这个平面的一条斜线垂直，那么它也和这条斜线在这个平面内的射影垂直.
方法技巧1.证明线面垂直的常用方法
2.证明线线垂直的常用方法
（1）利用线面垂直的性质证明线线垂直；
（3）平面几何中常见的垂直，如直径所对的圆周角为直角，菱形对角线相互垂直等.
3.证明线面垂直的关键是证明线线垂直，而证明线线垂直则需借助线面垂直的性质．
三垂线定理:平面内的一条直线如果和穿过这个平面的一条斜线在这个平面内的射影垂直,那么它也和这条斜线垂直.三垂线定理的逆定理:平面内的一条直线如果和穿过这个平面的一条斜线垂直,那么它也和这条斜线在这个平面内的射影垂直.
A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
解后反思用几何法求线面角时，若线面角不易找到，则可以用等体积法求解，此时的目标是求出直线上一点到平面的距离，它的好处是不需要找到此点在平面上的射影，运用本方法时一般需先找到一个对应的三棱锥，再转换三棱锥的顶点，根据等体积法求高.
二面角与两个平面的夹角
二面角的大小可以用它的平面角来度量,二面角的平面角是多少度,就说这个二面角是多少度.二面角的平面角的取值范围是⑥______.平面角是直角的二面角叫做直二面角.
二级结论三垂线定理平面内的一条直线如果与穿过这个平面的一条斜线在这个平面上的射影垂直，那么它也与这条斜线垂直.三垂线定理的逆定理:平面内的一条直线如果与穿过该平面的一条斜线垂直，那么它也垂直于这条斜线在平面内的射影.用定义法作二面角的平面角，经常会用到三垂线定理及其逆定理.此时请特别关注线面垂直或面面垂直的信息，因为若能找到一个半平面内的一个点在另一个半平面上的射影，那么借助三垂线定理或其逆定理，构造二面角的平面角就非常简单了.
（1）平面与平面垂直的定义一般地，两个平面相交，如果它们所成的二面角是⑥__________，就说这两个平面互相垂直.
（2）平面与平面垂直的判定定理和性质定理
方法技巧证明面面垂直的方法
（1）利用面面垂直的定义，即判定两平面所成的二面角为直二面角，将证明面面垂直的问题转化为证明二面角的平面角为直角的问题.
方法技巧要证面面垂直，需要在其中一个平面内找到一条直线证明其与另一个平面垂直，而此类线面垂直的证明，一般有两个思路:一是根据题目中的垂直关系，利用线面垂直的判定定理证明；二是根据面面垂直的性质定理证明.