艺考生教学课件32空间向量的应用-2024-2025学年高考数学艺体生一轮复习课件

这是一份艺考生教学课件32空间向量的应用-2024-2025学年高考数学艺体生一轮复习课件，共60页。PPT课件主要包含了利用空间向量求线线角，利用空间向量求线面角，利用空间向量求二面角，教材知识萃取，教材素材变式，模型解读，应用专练等内容，欢迎下载使用。
利用空间向量研究直线、平面的位置关系
利用空间向量求空间距离
基于长方体模型渗透数学建模思想
1.直线的方向向量和平面的法向量
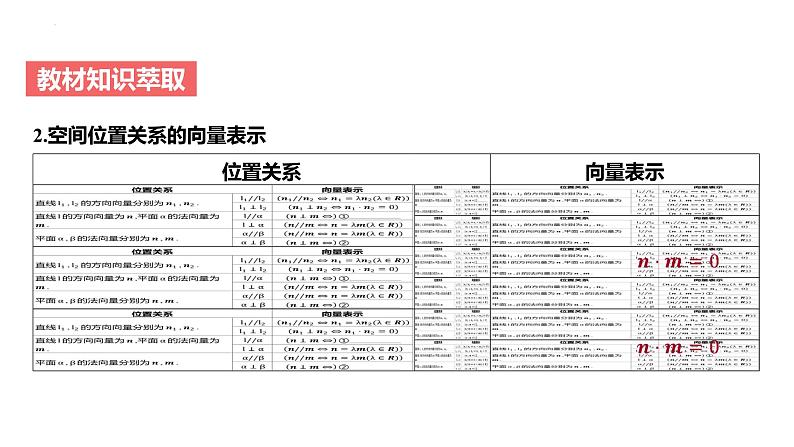
2.空间位置关系的向量表示
（1）直接法：观察是否有垂直于平面的直线，若有，则此直线的方向向量就是平面的法向量.
1.利用空间向量证明平行问题的方法
2.利用空间向量证明垂直问题的方法
注意 用向量法证明平行与垂直问题时，要注意解题的规范性.如证明线面平行时，需要说明一条直线在平面内，另一条直线在平面外.
1.［多选］［苏教选必二P31练习第1,2题变式］给出下列命题，其中是真命题的是( )
方法技巧求异面直线所成角的方法
解后反思求线线角时，若不易建系，且从题干条件中可以得到三条长度已知的棱，并且这三条棱两两之间的夹角均已知，也符合空间的一个基底的条件，则可以考虑用基底法求解.
方法技巧求直线与平面所成角的方法
方法技巧求二面角常用的方法
易错警示求二面角的正弦值的易错点：一是求平面的法向量出错，应注意点的坐标的求解的准确性；二是公式用错，把线面角的向量公式与二面角的向量公式搞混，导致结果出错；三是空间想象能力不足而失分，当求出两个法向量的夹角的余弦值时，误以为是所求二面角的余弦值，因忽视对二面角是锐角或钝角的判断，导致所得结果出错.
求点到平面的距离的常用方法