天津市2023_2024学年高一数学上学期期中试题含解析

这是一份天津市2023_2024学年高一数学上学期期中试题含解析，共10页。试卷主要包含了单项选择，填空题，解答题等内容，欢迎下载使用。
一、单项选择（每题 5 分，共 50 分.每题仅有一个正确选项，请将正确选项写到答题卡上）
1. 设全集，集合，则（）
A. B. C. D.
【答案】C
【解析】
【分析】根据集合运算定义先求并集，再求补集即得．
【详解】因为全集，集合，
所以，
所以．
故选：C．
2. 命题“”的否定是（）
A. B.
C. D.
【答案】B
【解析】
【分析】由全称量词命题的否定是存在量词命题求解即可
【详解】命题“”的否定是，
，
故选：B
3. 如果，则正确的是（）
A. 若a>b，则B. 若a>b，则
C. 若a>b，c>d，则a+c>b+dD. 若a>b，c>d，则ac>bd
【答案】C
【解析】
【分析】根据不等式的性质即可逐一求解.
【详解】对于A:取则，故A错，
对于B:若，则，故B错误，
对于C:由同号可加性可知：a>b，c>d，则a+c>b+d，故C正确，
对于D:若，则，，故D错误.
故选：C
4. 设，则“”是“”的
A. 充分而不必要条件
B. 必要而不充分条件
C. 充要条件
D. 既不充分也不必要条件
【答案】B
【解析】
【分析】
分别求出两不等式的解集，根据两解集的包含关系确定.
【详解】化简不等式，可知推不出；
由能推出，
故“”是“”的必要不充分条件，
故选B．
【点睛】本题考查充分必要条件，解题关键是化简不等式，由集合的关系来判断条件．
5. 下列各组函数是同一个函数的是（）
A. 与B. 与
C. 与D. 与
【答案】B
【解析】
【分析】根据函数相等的定义，逐个选项进行判断可得答案.
【详解】对于A，的定义域为，的定义域为，故两函数不相等，A错误；
对于B，与的定义域和解析式一致，故两函数相等，两函数为同一函数，B正确；
对于C，的定义域为，的定义域为，故两函数不相等，C错误；
对于D，与定义域相等，但是解析式不相等，故两函数不相等，D错误；
故选：B
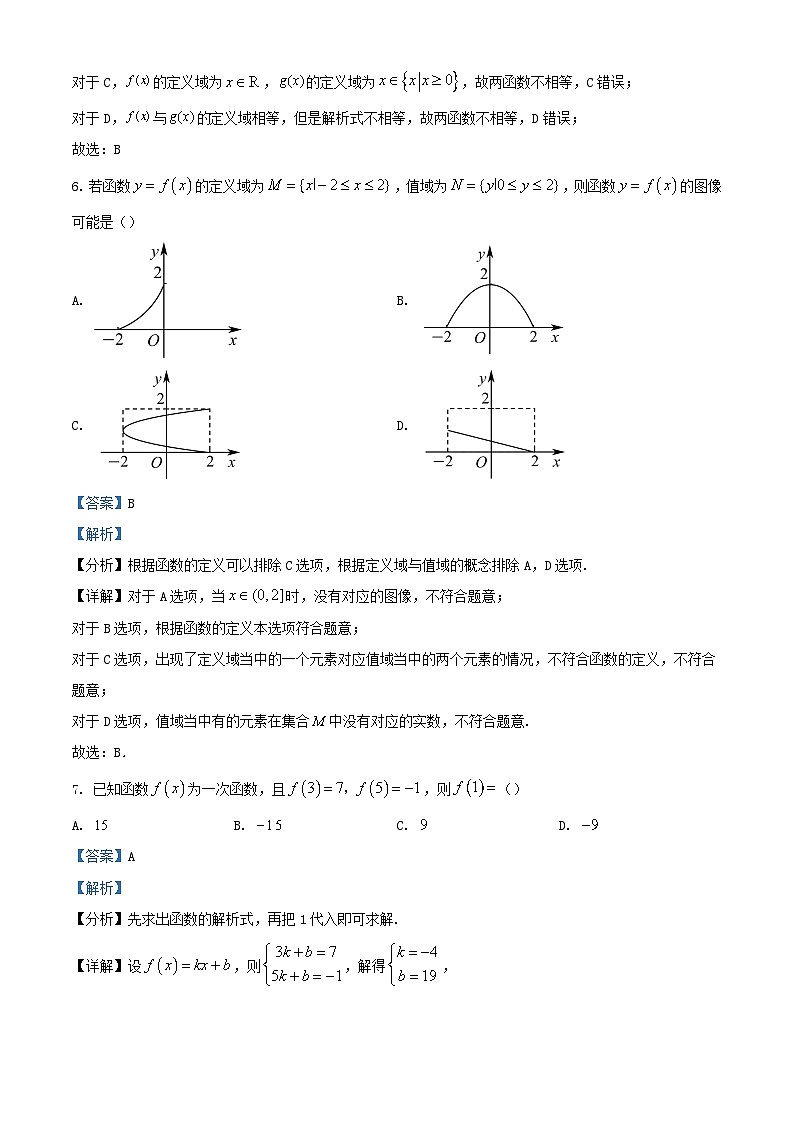
6. 若函数的定义域为，值域为，则函数的图像可能是（）
A. B.
C. D.
【答案】B
【解析】
【分析】根据函数的定义可以排除C选项，根据定义域与值域的概念排除A，D选项.
【详解】对于A选项，当时，没有对应的图像，不符合题意；
对于B选项，根据函数的定义本选项符合题意；
对于C选项，出现了定义域当中的一个元素对应值域当中的两个元素的情况，不符合函数的定义，不符合题意；
对于D选项，值域当中有的元素在集合中没有对应的实数，不符合题意.
故选：B．
7. 已知函数为一次函数，且，则（）
A. B. C. D.
【答案】A
【解析】
【分析】先求出函数的解析式，再把1代入即可求解.
【详解】设，则，解得，
，．
故选：A
8. 设函数若，且，则最小值为（）
A. B. C. D.
【答案】B
【解析】
【分析】根据条件得到，将变形为，再利用基本不等式即可求出结果.
【详解】因为，，
所以，即，又，
所以，
当且仅当，即时取等号，
故选：B.
9. 如图中的文物叫做“垂鳞纹圆壶”，是甘肃礼县出土的先秦时期的青铜器皿，其身流线自若、纹理分明，展现了古代中国精湛的制造技术．科研人员为了测量其容积，以恒定的流速向其内注水，恰好用时30秒注满，设注水过程中，壶中水面高度为h，注水时间为t，则下面选项中最符合h关于t的函数图象的是（）
A. B.
C. D.
【答案】A
【解析】
【分析】根据壶的结构，即可得出选项.
【详解】解：由文物的形状知，两头细中间粗，在注水过程中，以恒定的流速向其内注水，
前段部分注水高度逐渐递增，但增长速度逐步变慢，当超过中间部分，注水高中继续递增，但增长速度逐步变快，
对应图象满足条件.
故选：．
10. 已知，，若恒成立，则实数的取值范围是
A. 或B. 或
C. D.
【答案】C
【解析】
【分析】利用基本不等式求的最小值为，由恒成立得到，解不等式得到的范围.
【详解】因为，等号成立当且仅当，
所以，解得：.
【点睛】利用基本不等式求最值，注意“一正、二定、三等”三个条件，要确保等号能取到.
第Ⅱ卷（共 70 分）
二、填空题（每题 5 分，共 30 分.）
11. 函数的定义域是_______________.
【答案】
【解析】
【分析】列出需满足的不等式，再取交集即为函数定义域.
【详解】由题意，，解得且，
所以定义域为，
故答案：
12. 已知函数，若则a的值为______．
【答案】-2或1
【解析】
【分析】把a代入函数表达式解方程即可得出结果.
【详解】由，解得或者，
故答案为：-2或1.
13. 不等式的解集是______．
【答案】
【解析】
【分析】移项变形，结合判别式可得答案.
【详解】将移项变形可得，
因为，所以不等式无解，
故答案为：.
14. 已知集合，，则______．
【答案】
【解析】
【分析】解不等式求出集合、，再求交集即可.
【详解】集合，
，
则.
故答案为：.
15. 已知命题p：，是假命题，则实数的取值范围为___________．
【答案】
【解析】
【分析】根据条件，将问题转化成恒成立，分和两种情况讨论，即即可求出结果.
【详解】因为，是假命题，所以，对，都有，
当时，恒成立，
当时，则有，即，解得，
综上，实数的取值范围为，
故答案为：
16. 某公司建造一间背面靠墙的房屋，地面面积为48 m2，房屋正面每平方米造价为1200元，房屋侧面每平方米的造价为800元，屋顶的造价为5800元．如果墙高为3 m，且不计房屋背面和地面的费用，那么房屋的总造价最低为______元．
【答案】
【解析】
【分析】求出房屋的总造价，利用基本不等式可得答案.
【详解】设房屋底面一边长为m，则另一边长为m，
所以房屋的总造价为，
因为，所以，
当且仅当即时等号成立.
故答案为：.
三、解答题（共 40 分.）
17. 已知全集，，，
或.
（1）求，；
（2）求，.
【答案】（1），；
（2）或，或.
【解析】
【分析】
（1）根据集合交集、并集的概念进行计算即可；
（2）先计算集合B的补集，然后分别计算，.
【详解】解：（1）∵，，
∴，.
（2）或，或，
或.
【点睛】本题考查集合间的综合运算，较简单，解答时注意端点的取值.
18. 函数，集合．
（1）求函数的定义域；
（2）若，求实数的取值范围．
【答案】（1）
（2）
【解析】
【分析】（1）根据函数解析式，即可得到，从而求出结果；
（2）由，得到，再利用集合间的包含关系即可求出结果.
【小问1详解】
因为，所以，解得，
所以函数的定义域为.
【小问2详解】
因为，即，
又，易知，所以，解得，
所以，实数的取值范围为.
19. 已知函数，.
（1）若函数的图象经过点，求不等式的解集；
（2）若关于的不等式对一切实数都成立，求的取值范围.
【答案】（1）
（2）
【解析】
【分析】（1）根据条件得到，从而得到，再因式分解即可求出结果；
（2）利用一元二次函数与一元二次不等式间的关系即可求出结果.
【小问1详解】
因为函数的图象经过点，所以，得到，
所以，即，得到，
所以不等式的解集为.
【小问2详解】
因为对一切实数都成立，
所以，得到，解得，
故实数的取值范围为.
20. 已知函数．
（1）若关于的不等式的解集为，求，的值；
（2）当时，解关于的不等式．
【答案】（1）；（2）答案见解析.
【解析】
分析】
（1）由一元二次不等式的解集与一元二次方程根的关系，结合韦达定理可构造方程组求得结果；
（2）分别在、和三种情况下，解一元二次不等式求得结果.
【详解】（1）的解集为，方程的两根为和，
由韦达定理知：，解得：.
（2）当时，，
当时，的解集为；
当时，的解集为；