高中人教A版 (2019)6.2 平面向量的运算一课一练

这是一份高中人教A版 (2019)6.2 平面向量的运算一课一练，文件包含人教A版高中数学必修第二册导学案621向量的加法运算解析版doc、人教A版高中数学必修第二册导学案621向量的加法运算原卷版doc等2份试卷配套教学资源，其中试卷共15页， 欢迎下载使用。
本节内容选自《普通高中数学必修第一册》人教A版（2019）
第六章 平面向量及其应用
6.2.1向量的加法运算
学习目标：
1.借助实例掌握平面向量加法运算及运算规则，培养数学抽象的核心素养；
2.理解平面向量加法运算的几何意义，提升数学抽象的核心素养；
3.会用向量加法的三角形法则和平行四边形法则作两个向量的和向量，提升直观想象的核心素养。
学习重难点：
重点：理解并掌握向量加法的三角形法则和平行四边形法则
难点：向量加法的几何意义及运算律
自主预习：
本节所处教材的第 页.
复习——
平面向量的概念：
向量的模：
力的合成：
3.预习——
向量的加法：
三角形法则：
平行四边形法则：
运算律：
新课导学
学习探究
（一）新知导入
1. 创设情境，生成问题
①飞机从广州飞往上海，再从上海飞往北京(如图)，这两次位移的结果与飞机从广州直接飞往北京的位移是相同的．
②有两条拖轮牵引一艘轮船，它们的牵引力分别是F1＝3 000 N，F2＝2 000 N，牵引绳之间的夹角为θ＝60°(如图)，如果只用一条拖轮来牵引，也能产生跟原来相同的效果．
【想一想】从物理学的角度，上面实例中位移、牵引力说明了什么？体现了向量的什么运算？
探索交流，解决问题
【思考1】上述实例中位移的和运算、力的和运算分别用什么法则？

（二）向量的加法运算
1.向量加法的定义：求两个向量 的运算，叫做向量的加法。
对于零向量与任一向量a，规定：a＋0＝ ＝ .
【思考】两个向量的和还是向量吗？
2.向量的加法运算法则
（1）三角形法则
已知非零向量a，b，在平面上任取一点A，作eq \(AB,\s\up6(→))＝a，eq \(BC,\s\up6(→))＝b，则 叫做a与b的和，记作a＋b，即a＋b＝eq \(AB,\s\up6(→))＋eq \(BC,\s\up6(→))＝eq \(AC,\s\up6(→)).这种求向量和的方法，称为向量加法的 。
记忆口诀： ．
【思考1】若向量和共线，它们的和向量能否用三角形法则作出？
【思考2】如果eq \(AB,\s\up6(→))＋eq \(BC,\s\up6(→))＋eq \(CA,\s\up6(→))＝0，那么A，B，C三点一定能构成三角形吗？
（2）平行四边形法则
已知两个不共线向量a，b，作eq \(OA,\s\up6(→))＝a，eq \(OB,\s\up6(→))＝b，以 为邻边作▱OACB，则以O为起点的向量eq \(OC,\s\up6(→))就是向量a与b的和．这种作两个向量和的方法叫做向量加法的 。
记忆口诀：
【探究1】根据向量加法的三角形法则以及“三角形中两边之和大于第三边,两边之差小于第三边”,你能发现|a＋b|与|a|，|b|之间的关系吗?
【做一做】如果=8，=5，那么的取值范围为 .
【探究2】三角形法则和平行四边形法则的使用条件有何不同？
（3）加法的运算律
如图(1)在平行四边形ABCD中，，所以
在图(2)中，
所以
【探究3】实数的加法满足哪些运算律?向量的加法是否也满足这些运算律?
(1)交换律：a＋b＝ .
(2)结合律：(a＋b)＋c＝ .
（三）典型例题
1.向量加法法则的应用
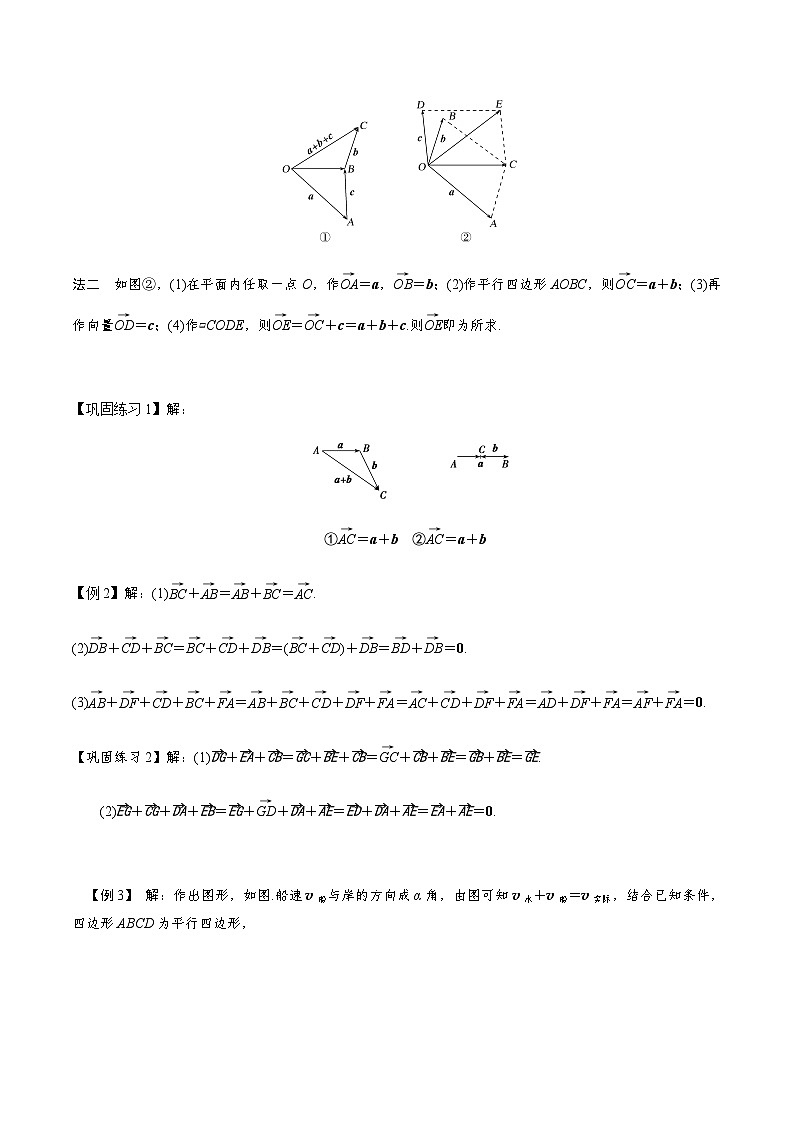
例1.如图，已知向量a，b，c，求作和向量a＋b＋c.
【类题通法】应用三角形法则、平行四边形法则作向量和时需注意的问题：
(1)三角形法则可以推广到n个向量求和，作图时要求“首尾相连”．即n个向量首尾相连的向量的和对应的向量是第一个向量的起点指向第n个向量的终点的向量．
(2)平行四边形法则只适用于不共线的向量求和，作图时要求两个向量的起点重合．
(3)当两个向量不共线时，两个法则实质上是一致的，三角形法则作出的图形是平行四边形法则作出的图形的一半，在多个向量的加法中，利用三角形法则更为简便．如本题(2)法一比法二简单.
【巩固练习1】如图，已知a、b，求作a＋b.
2.平面向量的表示
例2.化简：(1)eq \(BC,\s\up6(→))＋eq \(AB,\s\up6(→))；
(2)eq \(DB,\s\up6(→))＋eq \(CD,\s\up6(→))＋eq \(BC,\s\up6(→))；
(3)eq \(AB,\s\up6(→))＋eq \(DF,\s\up6(→))＋eq \(CD,\s\up6(→))＋eq \(BC,\s\up6(→))＋eq \(FA,\s\up6(→)).
【类题通法】向量加法运算律的意义和应用原则
(1)意义：向量加法的运算律为向量加法提供了变形的依据，实现恰当利用向量加法法则运算的目的.实际上，由于向量的加法满足交换律和结合律，故多个向量的加法运算可以按照任意的次序、任意的组合来进行.
(2)应用原则：利用代数方法通过向量加法的交换律，使各向量“首尾相连”，通过向量加法的结合律调整向量相加的顺序.
【巩固练习2】如图，E，F，G，H分别是梯形ABCD的边AB，BC，CD，DA的中点，化简下列各式：
(1)eq \(DG,\s\up6(→))＋eq \(EA,\s\up6(→))＋eq \(CB,\s\up6(→))；
(2)eq \(EG,\s\up6(→))＋eq \(CG,\s\up6(→))＋eq \(DA,\s\up6(→))＋eq \(EB,\s\up6(→)).
3.向量加法在实际问题中的应用
例3.在静水中船的速度为20 m/min，水流的速度为10 m/min，如果船从岸边出发沿垂直于水流的航线到达对岸，求船行进的方向.
【变式探究1】 若例3条件不变，则经过3小时，该船的实际航程是多少km?
【变式探究2】 若例3的条件不变，改为若船沿垂直于水流的方向航行，求船实际行进的方向的正切值(相当于与河岸的夹角).
【类题通法】应用向量解决平面几何问题的基本步骤
(1)表示：用向量表示有关量，将所要解答的问题转化为向量问题.
(2)运算：应用向量加法的平行四边形法则和三角形法则，将有关向量进行运算，解答向量问题.
(3)还原：根据向量的运算结果，结合向量共线、相等等概念回答原问题.
【巩固练习3】一架救援直升飞机从A地沿北偏东60°方向飞行了40 km到达B地，再由B地沿正北方向飞行40 km到达C地，求此时直升飞机与A地的相对位置.
（四）操作演练 素养提升
1.已知四边形ABCD是菱形，则下列等式中成立的是( )
A.eq \(AB,\s\up6(→))＋eq \(BC,\s\up6(→))＝eq \(CA,\s\up6(→)) B.eq \(AB,\s\up6(→))＋eq \(AC,\s\up6(→))＝eq \(BC,\s\up6(→))
C.eq \(AC,\s\up6(→))＋eq \(BA,\s\up6(→))＝eq \(AD,\s\up6(→)) D.eq \(AC,\s\up6(→))＋eq \(AD,\s\up6(→))＝eq \(DC,\s\up6(→))
2.正方形ABCD的边长为1，则|eq \(AB,\s\up6(→))＋eq \(AD,\s\up6(→))|为( )
A.1 B.eq \r(2) C.3 D.2eq \r(2)
3.化简eq \(AE,\s\up6(→))＋eq \(EB,\s\up6(→))＋eq \(BC,\s\up6(→))等于( )
A.eq \(AB,\s\up6(→)) B.eq \(BA,\s\up6(→)) C.0 D.eq \(AC,\s\up6(→))
4.小船以10eq \r(3) km/h的静水速度按垂直于对岸的方向行驶，同时河水的流速为
10 km/h，则小船实际航行速度的大小为________ km/h.
课堂小结
通过这节课，你学到了什么知识？


在解决问题时，用到了哪些数学思想？



学习评价
【自我评价】 你完成本节导学案的情况为（ ）
A.很好 B.较好 C.一般 D.较差
【导学案评价】 本节导学案难度如何（ ）
A.很好 B.较好 C.一般 D.较差
【建议】 你对本节导学案的建议：

课后作业
完成教材：第10页 练习 第1，2，3,4,5题
第22 页 习题6.2 第1,2,3题