高中数学人教A版 (2019)必修 第二册9.2 用样本估计总体同步达标检测题

这是一份高中数学人教A版 (2019)必修 第二册9.2 用样本估计总体同步达标检测题，文件包含人教A版高中数学必修第二册导学案921总体取值规律的估计解析版doc、人教A版高中数学必修第二册导学案921总体取值规律的估计原卷版doc等2份试卷配套教学资源，其中试卷共16页， 欢迎下载使用。
地 位：
本节内容选自《普通高中数学必修第二册》人教A版（2019）
第九章 统计
9.2 用样本估计总体
学习目标：
1.掌握频率分布表的作法以及频率分布直方图的画法，培养数学抽象的核心素养；
2. 掌握用频率分布直方图估计总体，培养数据分析的核心素养；
3.能根据频率分布表和频率分布直方图观测数据的分布规律，培养数据分析的核心素养。
学习重难点：
1.重点：列频率分布表，画频率分布直方图
2.难点：根据频率分布表和频率分布直方图观测数据的分布规律
自主预习：
本节所处教材的第 页.
复习——
总体、样本、样本容量：
初中学过的统计图：
预习——
频率分布表：
频率分布直方图：
新课导学
学习探究
（一）新知导入
下面按时间顺序(从1789年的华盛顿到2017年的特朗普，共45任)给出了历届美国总统就任时的年龄：57，61，57，57，58，57，61，54，68，51，49，64，50，48，65，52，56，46，54，49，51，47，55，55，54，42，51，56，55，51，54，51，60，62，43，55，56，61，52，69，64，46，54，48，70.
问题 你能很容易地看出这些数据有什么规律吗？若不能，对这些数据如何处理才可以？
（二）总体取值规律的估计
知识点一 画频率分布直方图的步骤
(1)求极差：极差是一组数据中最大值与最小值的差；
(2)决定组距与组数：当样本容量不超过100时，常分成5～12组，为了方便起见，一般取等长组距，并且组距应力求“取整”．
(3)将数据分组．
(4)列频率分布表：一般分四列：分组、频数累计、频数、频率．其中频数合计应是样本容量，频率合计是1.
(5)画频率分布直方图：横轴表示分组，纵轴表示eq \f(频率,组距).小长方形的面积＝组距×eq \f(频率,组距)＝频率．各小长方形的面积和等于1.
【探究1】为什么要对样本数据进行分组？
【探究2】频数分布表与频率分布直方图有什么不同？
知识点二 其它统计图表
【思考】除了频率分布直方图，初中我们还学习了哪些图表呢？
【辩一辩】判断(正确的打“√”，错误的打“×”)
1.频率分布直方图中小长方形的高表示该组上的个体在样本中出现的频率与组距的比值.( )
2.频率分布直方图中小矩形的面积表示该组的个体数.( )
3.扇形统计图表示的是比例，条形统计图不表示比例.( )
（三）典型例题
1.画频率分布直方图
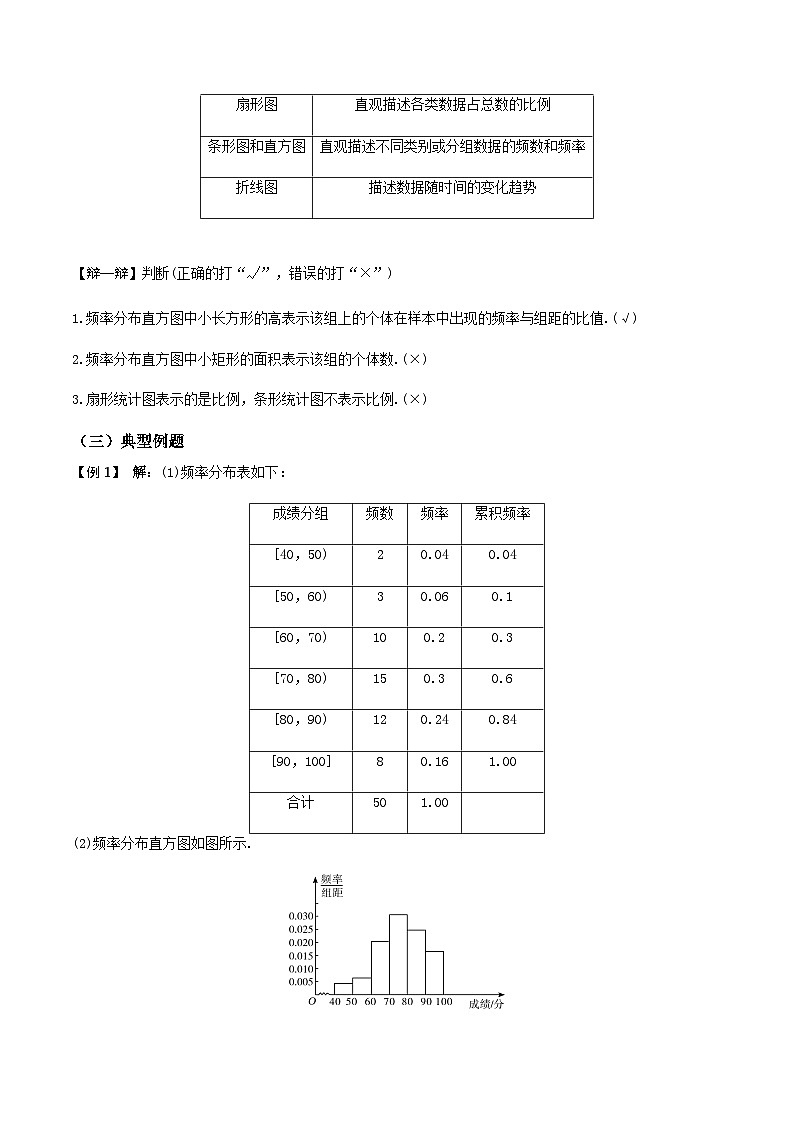
例1. 从某校高三学生中抽取50名参加数学竞赛，成绩分组(单位：分)及各组的频数如下：
[40，50)，2；[50, 60)，3；[60, 70), 10；[70, 80), 15；[80，90)，12；[90，100]，8.
(1)列出样本的频率分布表(含累积频率)；
(2)画出频率分布直方图；
【类题通法】绘制频率分布直方图的注意点
(1)各组频率的和等于1，因此，各小矩形的面积的和也等于1；
(2)频率分布直方图比频率分布表更直观、形象地反映了样本的分布规律；
(3)在xOy坐标平面内画频率分布直方图时，x＝样本数据，y＝eq \f(频率,组距)，这样每一组的频率可以用该组的组距为底、eq \f(频率,组距)为高的小矩形的面积来表示.其中，矩形的高＝eq \f(频率,组距)＝eq \f(1,组距×样本容量)×频数；
(4)同样一组数据，如果组距不同，横轴、纵轴单位不同，得到的频率分布直方图的形状也会不同；
(5)同一个总体，由于抽样的随机性，如果随机抽取另外一个相同容量的样本，所形成的样本频率分布直方图一般会与前一个样本频率分布直方图有所不同，但它们都可以近似地看做总体的分布.
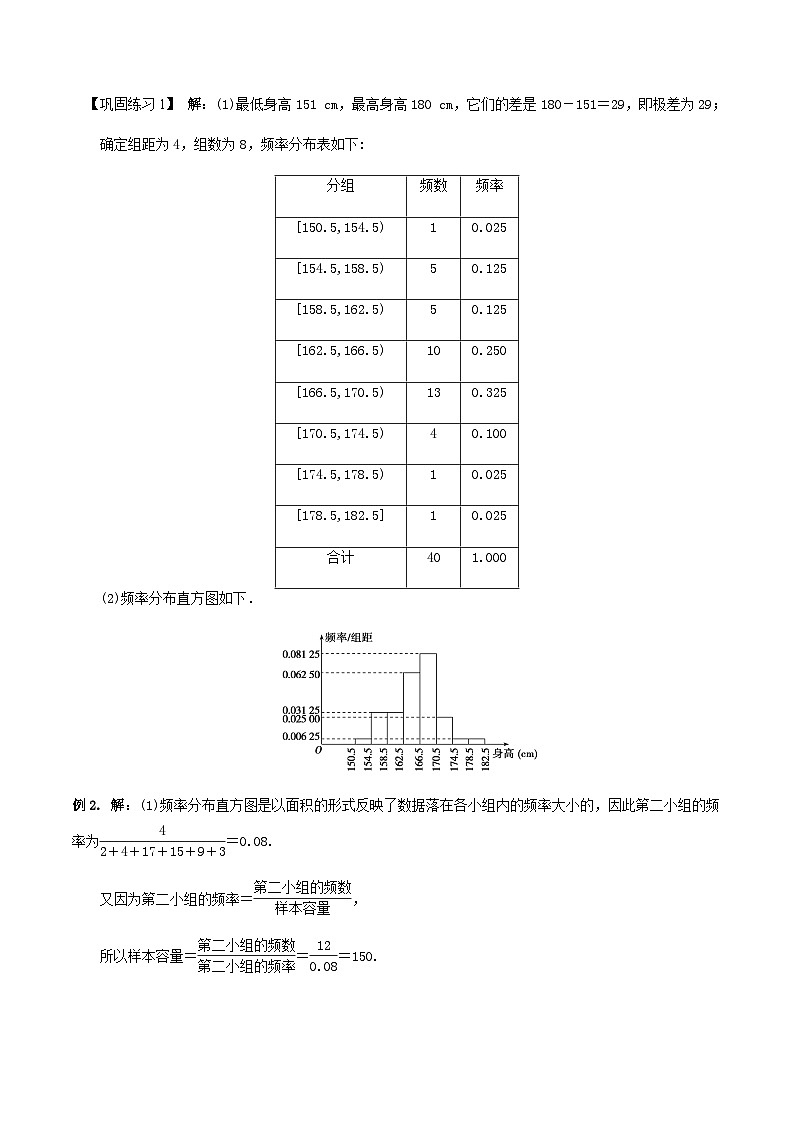
【巩固练习1】调查某校高一年级男生的身高，随机抽取40名高一男生，实测身高数据(单位：cm)如下：
171 163 163 166 166 168 168 160 168 165 171 169 167 169 151 168 170 168 160 174 165 168 174 158 167 156 157 164 169 180 176 157 162 161 158 164 163 163 167 161
(1)作出频率分布表；
(2)画出频率分布直方图．
2.频率分布直方图的应用
例2.为了了解高一年级学生的体能情况，某校抽取部分学生进行一分钟跳绳次数测试，将所得数据整理后，画出频率分布直方图(如图所示)，图中从左到右各小矩形的面积之比为2∶4∶17∶15∶9∶3，第二小组的频数为12.
(1)第二小组的频率是多少？样本容量是多少？
(2)若次数在110以上(含110次)为达标，则该校全体高一年级学生的达标率是多少？
【变式1】 (变结论)在例2条件下，试求样本中不达标的学生人数.
【变式2】 (变结论)在例2条件下，试求次数在130以上(含130次)的学生人数.
【类题通法】由频率分布直方图进行相关计算时，需掌握下列关系式：
(1)eq \f(频率,组距)×组距＝频率.
(2)eq \f(频数,样本容量)＝频率，此关系式的变形为：样本容量×频率＝频数.
【巩固练习2】某校100名学生期中考试语文成绩(单位：分)的频率分布直方图如图所示，其中成绩分组区间是[50，60)，[60，70)，[70，80)，[80，90)，[90，100].
(1)求图中a的值；
(2)若这100名学生的语文成绩在某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示，求数学成绩在[50，90)之外的人数.
3.条形图、折线图、扇形图的应用
例3.如图是根据某市3月1日至3月10日的最低气温(单位：℃)的情况绘制的折线统计图，试根据折线统计图反映的信息，绘制该市3月1日到10日最低气温(单位：℃)的扇形统计图和条形统计图.
【类题通法】1.条形图是用一个单位长度表示一定的数量或频率，根据数量的多少或频率的大小画成长短不同的矩形条，条形图能清楚地表示出每个项目的具体数目或频率.
2.扇形图是用整个圆面积表示总数(100%)，用圆内的扇形面积表示各个部分所占总数的百分数.
3.在画折线图时，要注意明确横轴、纵轴的实际含义.
【巩固练习3】某厂生产一种产品，图①是该厂第一季度三个月产量的统计图，图②是这三个月的产量与第一季度总产量的比例分布统计图，统计员在制作图①，图②时漏填了部分数据．根据上述信息，回答下列问题：
(1)该厂第一季度________月的产量最高．
(2)该厂一月份产量占第一季度总产量的________%.
(3)该厂质检科从第一季度的产品中随机抽样，抽检结果发现样品的合格率为98%.请你估计：该厂第一季度大约生产了多少件合格的产品？(写出解答过程)
（四）操作演练 素养提升
1.200辆汽车经过某一雷达地区，时速的频率分布直方图如图所示，则时速超过60 km/h(含60 km/h)的汽车数量为( )
A.65辆 B.76辆 C.88辆 D.95辆
2.将容量为n的样本中的数据分成6组，绘制频率分布直方图，若第一组至第六组的频率之比为2∶3∶4∶6∶4∶1，且前三组数据的频数之和等于27，则n＝________.
3.如图是甲、乙、丙、丁四组人数的扇形统计图的部分结果，根据扇形统计图的情况可以知道丙、丁两组人数和为( )
A.250B.150C.400D.300
4.甲、乙两个城市2018年4月中旬每天的最高气温统计图如图所示，则这9天里，气温比较稳定的是________城市(填“甲”“乙”).
课堂小结
通过这节课，你学到了什么知识？


在解决问题时，用到了哪些数学思想？



学习评价
【自我评价】 你完成本节导学案的情况为（ ）
A.很好 B.较好 C.一般 D.较差
【导学案评价】 本节导学案难度如何（ ）
A.很好 B.较好 C.一般 D.较差
【建议】 你对本节导学案的建议：

课后作业
完成教材：第197页 练习 第1，2,3题
第201页 练习 第1，2题
第214页 习题9.2 第1题
统计图表
主要应用
扇形图
直观描述各类数据占总数的比例
条形图和直方图
直观描述不同类别或分组数据的频数和频率
折线图
描述数据随时间的变化趋势