高中数学人教A版 (2019)必修 第二册7.2 复数的四则运算达标测试

这是一份高中数学人教A版 (2019)必修 第二册7.2 复数的四则运算达标测试，文件包含人教A版高中数学必修第二册同步讲与练第03讲721复数的加减运算及其几何意义原卷版doc、人教A版高中数学必修第二册同步讲与练第03讲721复数的加减运算及其几何意义解析版doc等2份试卷配套教学资源，其中试卷共29页， 欢迎下载使用。

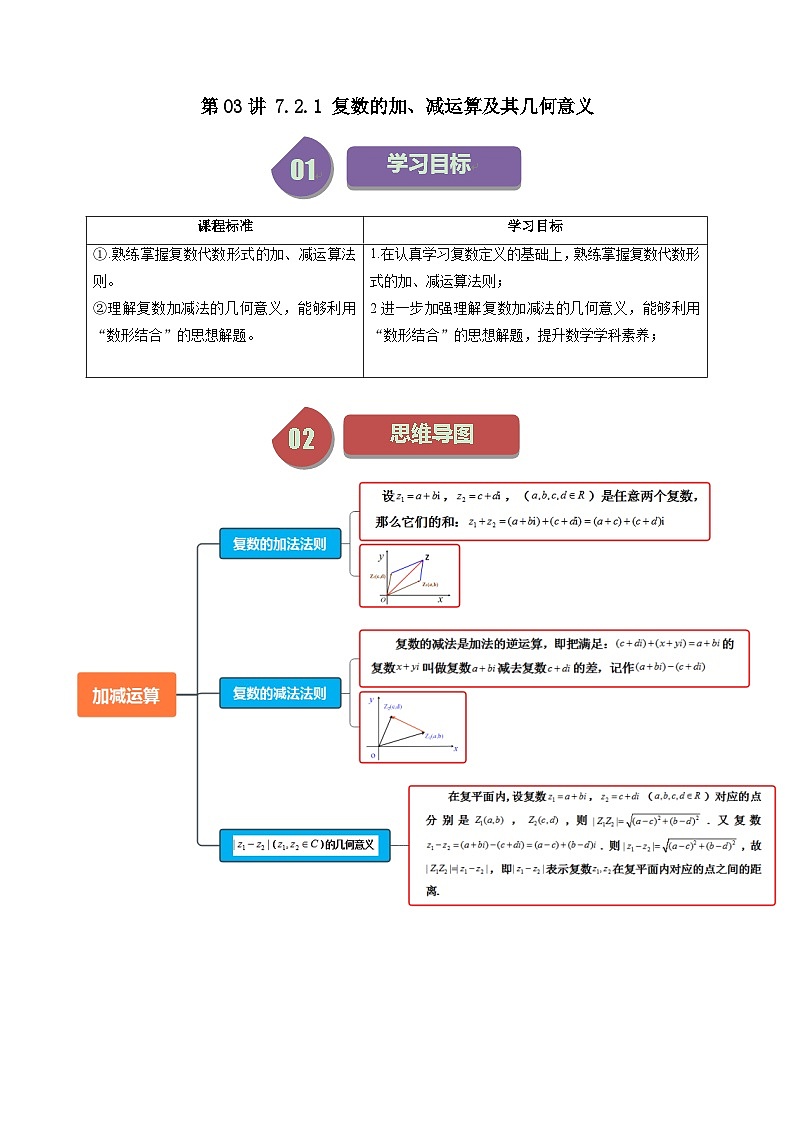
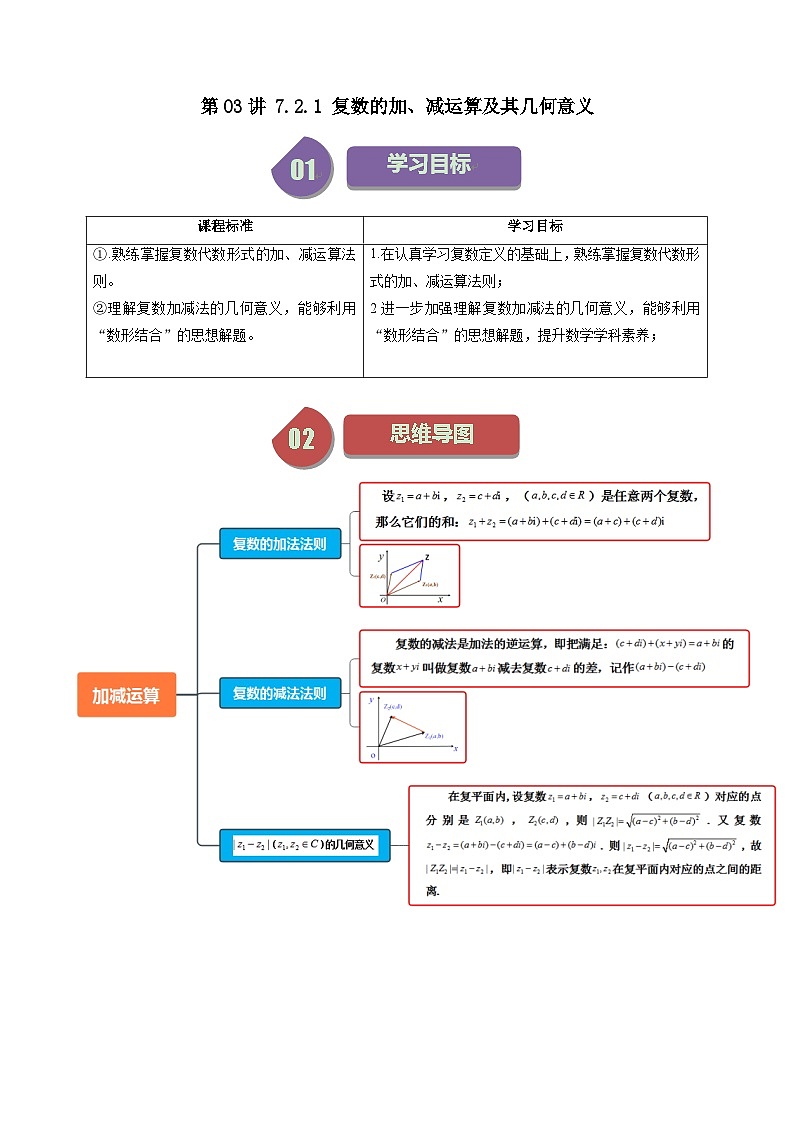
知识点01：复数代数形式的加法运算及其几何意义
（1）复数的加法法则
设，，（）是任意两个复数，那么它们的和：
显然：两个复数的和仍然是一个确定的复数
（2）复数加法满足的运算律
对任意，有
交换律：
结合律：
（3）复数加法的几何意义
如图，设在复平面内复数，对应的向量分别为，，以，为邻边作平行四边形，则，即：
，即对角线表示的向量就是与复数对应的向量.所以：复数的加法可以按照向量的加法来进行.
【即学即练1】（2022·高一课时练习）复数的加、减法运算法则
设，
则 ，
．
复数加法的运算律
（1）交换律： ．
（2）结合律： ．
复数加、减法的几何意义
如图，设在复平面内复数对应的向量分别为，以为邻边作平行四边形，则与对应的向量是 ，与对应的向量是 ．
【答案】
知识点02：复数代数形式的减法运算及其几何意义
（1）复数的减法法则
类比实数集中减法的意义，我们规定，复数的减法是加法的逆运算，即把满足：的复数叫做复数减去复数的差，记作
注意：①两个复数的差是一个确定的复数；
②两个复数相加减等于实部与实部相加减，虚部与虚部相加减.
（2）复数减法的几何意义
复数 向量
【即学即练2】（2018·高三课时练习）如图在复平面上，一个正方形的三个顶点对应的复数分别是，那么这个正方形的第四个顶点对应的复数为（ ）．
A．B．C．D．
【答案】D
【解析】利用复数的几何意义、向量的平行四边形法则即可得出．
【详解】∵ ，
∴ 对应的复数为：，
∴点对应的复数为．
故选D．
知识点03：()的几何意义
在复平面内,设复数，（）对应的点分别是，,则.又复数.则,故，即表示复数在复平面内对应的点之间的距离.
【即学即练3】（2023·福建福州·福建省福州第一中学校考三模）已知复数，满足，，则的最大值为 .
【答案】4
【详解】设，
则，
所以，即，，
，
当时，则取得最大值，最大值为.
故答案为：4
题型01 复数的加、减运算
【典例1】（2023下·海南省直辖县级单位·高一校考期中）设复数，则复数在复平面内对应的点所在的象限是（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【答案】B
【详解】根据复数运算可知：，在复平面对应的点的坐标为，
位于第二象限.
故选：B
【典例2】（2023下·内蒙古呼伦贝尔·高一校考期末）已知复数，，则 ．
【答案】
【详解】因为复数，，则.
故答案为：.
【典例3】（2023·全国·高一随堂练习）计算：
(1)； (2)；
(3)； (4)．
【答案】(1) (2) (3) (4)
【详解】（1）
（2）
（3）
（4）
【变式1】（2023下·西藏林芝·高二校考期末）若复数，则 （ ）
A．B．C．D．
【答案】A
【详解】由复数，则.
故选：A.
【变式2】（2023下·北京昌平·高一统考期末）已知复数，则复数在复平面内对应的点位于第 象限.
【答案】三
【详解】因为，
所以，
所以复数在复平面内对应的点为，位于第三象限，
故答案为：三
【变式3】（2023·全国·高一随堂练习）计算：
(1)； (2)； (3)；
(4)； (5)；
(6)．
【答案】(1) (2)2 (3)0 (4) (5) (6)
【详解】（1）由题意可得：.
（2）由题意可得：.
（3）由题意可得：.
（4）由题意可得：.
（5）由题意可得：.
（6）由题意可得：.
题型02 复数的加、减运算的几何意义
【典例1】（2023下·河南郑州·高一中牟县第一高级中学校考阶段练习）复数与分别表示向量与，则表示向量的复数为（ ）
A．B．C．D．
【答案】D
【详解】复数与分别表示向量与，
因为，所以表示向量的复数为.
故选：D.
【典例2】（2022下·山东日照·高一校联考期末）若复数，（其中为虚数单位）所对应的向量分别为与，则的周长为 .
【答案】16
【详解】因为，，，
所以，，.
所以的周长为.
故答案为：16
【典例2】（2022·高一课时练习）如图所示,平行四边形的顶点O,A,C对应的复数分别为0,,,其中i为虚数单位由复数的几何意义,知与对应的复数分别为,.
(1)求对应的复数.
(2)求对应的复数.
(3)求对应的复数.
【答案】(1).(2).(3)
【详解】解：(1)因为,所以表示的复数为.
(2)因为,所以表示的复数为.
(3),所以对应的复数为.
【变式1】（2023·高一课时练习）复平面上有A、B、C三点，点对应的复数为，对应的复数为，对应的复数为，则点的坐标为 ．
【答案】
【详解】因为对应的复数是，对应的复数为，又，
所以对应的复数为，又，
所以点对应的复数为，
所以点的坐标为．
故答案为：．
【变式2】（2022下·高二课时练习）在复平面上，如果，对应的复数分别是，，那么对应的复数为 .
【答案】
【详解】对应的复数分别是，
对应的复数为.
故答案为：.
【变式3】（2022·高一课时练习）设向量及在复平面内分别与复数z1＝5＋3i及复数z2＝4＋i对应，试计算z1－z2，并在复平面内表示出来
【答案】z1－z2＝1＋2i，作图见解析.
【详解】解: z1－z2＝(5＋3i)－(4＋i)＝(5－4)＋(3－1)i＝1＋2i， ，则即为z1－z2所对应的向量，如图所示，
根据复数减法的几何意义：复数z1－z2是连接向量,的终点，并指向被减数的向量所对应的复数.
题型03 与复数的模的几何意义有关的应用
【典例1】（2023·江西·统考模拟预测）已知复数满足，则的最小值为（ ）
A．B．C．D．
【答案】B
【详解】设，
由得：，，
整理可得：，，
（当且仅当时取等号），的最小值为.
故选：B.
【典例2】（2023下·河北邢台·高一河北南宫中学校考阶段练习）已知是虚数单位，复数，，，且，则的最小值为（ ）
A．B．C．D．
【答案】B
【详解】因为，则，，
由可得，解得，则，
所以，，
因此，，当且仅当时，等号成立，
故的最小值为.
故选：B.
【典例3】（2022下·上海黄浦·高二上海市向明中学校考阶段练习）若(是虚数单位),则的最小值是（ ）
A．B．C．D．
【答案】D
【详解】解：由复数的几何意义可知：表示的点在单位圆上，
而|z−2−2i|表示该单位圆上的点到复数表示的点的距离，

由图象可知：的最小值应为点到的距离，
而 ，圆的半径为1，
故的最小值为，
故选D．
【变式1】（2022上·湖北武汉·高三校联考阶段练习）复数满足，则的范围是（ ）
A．B．C．D．
【答案】D
【详解】设，则，
由题意可得：，解得，
则.
故选：D.
【变式2】（2022·湖南岳阳·岳阳一中校考一模）若为虚数单位，复数满足，则的最大值为（ ）
A．B．C．D．
【答案】C
【详解】表示的几何意义是复数对应的点到原点的距离小于等于1，
表示的几何意义是复数对应的点与点连线段的长度，
故的最大值为，
故选：C.
【变式3】（2023·高一课时练习）若复数z满足|z﹣2i|＝1（i为虚数单位），则|z|的最小值为 .
【答案】1
【详解】设，
∵，
∴，
∴，
∴.
则.
当时取等号.
故答案为：1.
题型04 根据复数的加、减运算结果求参数
【典例1】（2022上·浙江·高三校联考开学考试）若，则的实部可能是（ ）
A．3B．1C．D．
【答案】A
【详解】设，
因为，
所以，得，
所以，
所以，
则的实部，
故选：A
【典例2】（2022·河北石家庄·石家庄一中校考模拟预测），若，则（ ）
A．B．C．D．
【答案】B
【详解】设，则，故，
故，故.
故选：.
【变式1】（2022上·安徽·高三校联考阶段练习）已知复数z满足，则z的虚部是（ ）
A．B．1C．D．i
【答案】A
【详解】设，
因为，可得，
则，可得，所以复数的虚部是.
故选：A
【变式2】（2022下·河南安阳·高一统考期末）已知，，其中为实数，为虚数单位，若，则的值为 ．
【答案】
【详解】由题意可得，即，
根据两个复数相等的充要条件可得，解得，
故答案为：.
题型05 根据复数的加、减运算结果求复数的特征
【典例1】（2023下·广东东莞·高一东莞市厚街中学校考阶段练习）如果一个复数的实部和虚部相等，则称这个复数为“等部复数”，若复数（其中）为“等部复数”，则复数在复平面内对应的点在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【答案】A
【详解】因为复数（其中）为“等部复数，可得，
即，可得，
则在复平面内对应的点为位于第一象限.
故选：A.
【典例2】（2023下·四川眉山·高一仁寿一中校考期中）复数对应的点在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【答案】B
【详解】由复数，可得复数在复平面内对应的点位于第二象限.
故选：B.
【典例3】（2023下·宁夏银川·高二宁夏育才中学校考期中）设复数，满足，，复数在复平面内所对应的点分别为A，B，C，则三角形的面积为（ ）
A．3B．C．2D．
【答案】D
【详解】设，，
则，
所以，，，，
所以，
即，
所以，
又，，
在中，过作，垂足为，
则为中点，即，
所以，
所以.
故选：D.

【变式1】（2023下·湖南邵阳·高一统考期末）实数时，复数在复平面内对应的点位于（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【答案】A
【详解】
又，故
故该复数在复平面内对应的点位于第一象限.
故选：
【变式2】（2022下·上海浦东新·高一校考期末）已知关于的实系数一元二次方程有两个虚根和，且，则的值为（ ）
A．2B．C．D．
【答案】C
【详解】因为方程有两个虚根和，
所以，则，
又由求根公式知两虚根为，，
所以，则，解得，满足要求，
所以.
故选：C.
【变式3】（2022下·上海宝山·高一上海交大附中校考期中）已知复数，满足，，，则在复平面所对应的点组成的图形的面积为 ．
【答案】
【详解】，是以复平面内点为圆心，以为半径的圆，
， ，
，即，
复数以复平面内点为圆心，半径为1和的两圆构成的圆弧，
则在复平面所对应的点组成的图形的面积为：
故答案为：.
A夯实基础 B能力提升
A夯实基础
一、单选题
1．（2023下·陕西安康·高三陕西省安康中学校考阶段练习）已知复数 ，且，其中a，b为实数，则（ ）
A．，B．，C．，D．，
【答案】B
【详解】因为 ，所以，
由，得 ，即 ；
故选：B.
2．（2022下·广西钦州·高二统考期末）等于（ ）
A．B．C．D．
【答案】D
【详解】.
故选：D.
3．（2023·西藏拉萨·统考一模）已知复数为纯虚数，则实数的值为（ ）
A．B．0C．1D．2
【答案】D
【详解】因为为纯虚数，
所以，解得.
故选：D．
4．（2023·贵州黔东南·统考一模）已知复数，，则的实部与虚部分别为（ ）
A．，B．，C．，D．，
【答案】A
【分析】应用复数加法求，根据实部、虚部定义得答案.
【详解】因为，，所以，其实部与虚部分别为，.
故选：A
5．（2023·全国·模拟预测）在复平面内，复数对应的点的坐标为，则（ ）
A．2B．C．D．
【答案】A
【分析】利用特殊角的三角函数值，结合复数的运算即可得解.
【详解】因为可化为，
所以点的坐标为，则，
所以，
所以．
故选：A．
6．（2023上·辽宁朝阳·高三校联考阶段练习）复数在复平面内对应的点位于（ ）
A．第一象限B．第二象限
C．第三象限D．第四象限
【答案】D
【分析】根据复数的运算可得，结合复数的几何意义分析判断.
【详解】由题意可得：，
所以该复数对应的点为，该点在第四象限.
故选：D.
7．（2023上·江苏南通·高三海安高级中学校考阶段练习）在复平面内，为原点，为虚数单位，复数对应的向量，则（ ）
A．3B．C．2D．
【答案】D
【分析】由复数的几何意义可得，再根据题意计算复数的模即可.
【详解】因为复数对应的向量，所以，
所以.
故选：.
8．（2023上·江苏盐城·高三校联考阶段练习）已知复数满足，当的虚部取最小值时，（ ）
A．B．C．D．
【答案】A
【分析】设，利用复数的模长公式可得出，求出的取值范围，可得出的最小值，进而可得出的值，由此可得出复数的值.
【详解】设，则，
所以，，即，
所以，，可得，解得，
当的虚部取最小值时，即当时，则，解得，
故，
故选：A.
二、多选题
9．（2023上·河北保定·高三定州市第二中学校考阶段练习）已知，为复数，则下列说法正确的是（ ）
A．若，则B．若，则
C．若，则D．若，则或
【答案】AC
【分析】根据共轭复数的定义、复数模的运算公式，结合复数减法的运算法则逐一判断即可.
【详解】A：根据共轭复数的定义，本选项正确；
B：取，，满足，但，故本选项错误；
C：设，，，由，得，即，，所以，即，故本选项正确；
D：取，，则，，此时且，故D不正确．
故选：AC
10．（2021下·山东济宁·高一统考期末）设复数的共轭复数为，为虚数单位，则下列命题正确的是（ ）
A．B．是纯虚数
C．若，则D．若，则的最大值为2
【答案】AD
【分析】利用复数的运算法则判断A的正误；复数的解法判断复数是实数，判断B；利用复数的模的运算法则判断C；利用复数模的几何意义判断D．
【详解】解：因为复数与其共轭复数为的实部相等，虚部互为相反数，所以，A正确；
当为实数时，也为实数，则是实数，B错误；
若，则，C错误；
若，设，即，则表示圆上的点到原点的距离，其最大值为2，D正确，
故选：AD．
三、填空题
11．（2023上·上海宝山·高三上海交大附中校考期中）复数，（a、），若它们的和为实数，差为纯虚数，则 ．
【答案】
【分析】应用复数的加减运算求、，根据实数、纯虚数定义求参数，进而求目标复数的模即可.
【详解】由题设为实数，故，
，故，
所以.
故答案为：
12．（2023·河南开封·统考二模）已知复数满足，写出一个满足条件的复数 ．
【答案】（答案不唯一，虚部为即可）
【分析】设复数，代入复数的模的公式求解即可.
【详解】设，（，），
则，
，
∵，∴，
∴，化简得，解得.
∴满足条件的一个复数（答案不唯一，虚部为即可）.
故答案为：（答案不唯一，虚部为即可）.
四、解答题
13．（2023·高一课时练习）计算：
(1)；
(2)；
(3).
【答案】(1)；
(2)-7
(3).
【分析】根据复数的加减运算法则即可求解
【详解】（1）；
（2）；
（3）.
14．（2023下·辽宁·高一校联考期末）已知复数，，．
(1)若是纯虚数，求；
(2)若，求．
【答案】(1)
(2)
【分析】（1）先计算，然后由其为纯虚数，可得实部为零，虚部不为零，从而可求出的值；
（2）由可复数为实数，则虚部为零，实部大于零，求出的值，从而可求出复数，进而可求得.
【详解】（1）由题意得，
因为是纯虚数，所以，得．
（2）因为，所以，得．
故．
B能力提升
1．（2023下·江西南昌·高一校联考阶段练习）已知复数满足．
(1)求；
(2)比较与的大小．
【答案】(1)
(2)
【详解】（1）设，
则由，得，
即，所以
解得，
所以．
（2），
，
因为，
所以，
所以．
2．（2023下·湖北武汉·高一湖北省水果湖高级中学校联考期末）（1）设，在复平面内对应的点为，那么求满足条件：的点的集合的图形面积；
（2）已知复数， ，且，求的范围.
【答案】（1）；（2）.
【详解】（1）由复数的几何意义知：满足条件的点的集合的图形为圆环，
其中大圆半径为，小圆半径为，
故所求面积为.
（2）因为， ，且，
所以，所以且，
故，
因为，，
所以当时，有最小值为，
所以范围为.
3．（2022下·江苏常州·高一常州市第二中学校考阶段练习）已知复数均为锐角，且.
(1)求的值；
(2)若，求的值.
【答案】(1)
(2)
【详解】（1）因为复数，所以.
所以
因为，所以，解得：.
（2）因为均为锐角，所以，
所以.
因为为锐角，，所以.
所以
.
课程标准
学习目标
①.熟练掌握复数代数形式的加、减运算法则。
②理解复数加减法的几何意义，能够利用“数形结合”的思想解题。
1.在认真学习复数定义的基础上，熟练掌握复数代数形式的加、减运算法则；
2进一步加强理解复数加减法的几何意义，能够利用“数形结合”的思想解题，提升数学学科素养；