





所属成套资源:北师大版(2024)七年级数学下册 全册课件
初中数学北师大版(2024)七年级下册(2024)第一章 整式的乘除3 乘法公式示范课课件ppt
展开
这是一份初中数学北师大版(2024)七年级下册(2024)第一章 整式的乘除3 乘法公式示范课课件ppt,共17页。PPT课件主要包含了a+ba-b,a2-b2,a+b,a-b,等面积法,-5a,2a2-8等内容,欢迎下载使用。
1. 掌握平方差公式的结构特征,能运用公式进行简便运算;(重点)2. 会用几何图形说明公式的意义,体会数形结合的思想方法.(难点)
1.平方差公式:(1)符号表达式: . (2)文字表达: .
2.判断下列算式能否运用平方差公式计算.(1)(a+2)(a- 3); (2)(- m- n)(m- n);(3)(2x+3y)(3x- 2y); (4)(4x- 3)(- 4x- 3).
(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积,等于这两个数的平方差
大家回顾一下上节课学习的平方差公式,看谁答得又对又快.
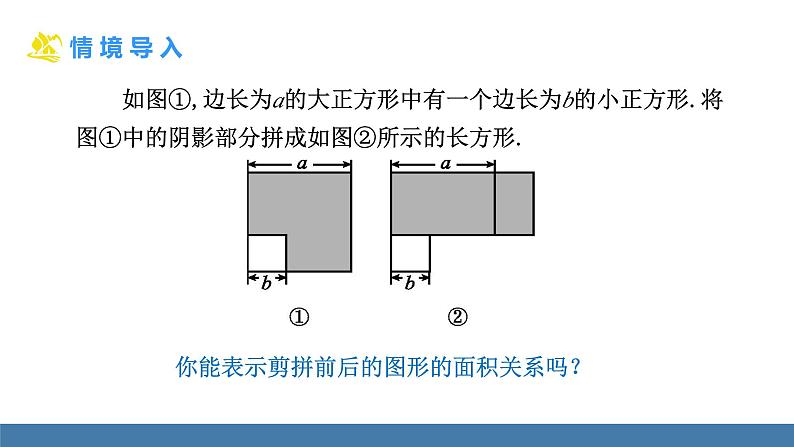
如图①,边长为a的大正方形中有一个边长为b的小正方形.将图①中的阴影部分拼成如图②所示的长方形.
你能表示剪拼前后的图形的面积关系吗?
(a+b)(a-b)=a2-b2
(4)对于图①阴影部分的面积,你还有其他计算方法吗?
如图,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形中阴影部分面积的关系,验证了公式 .
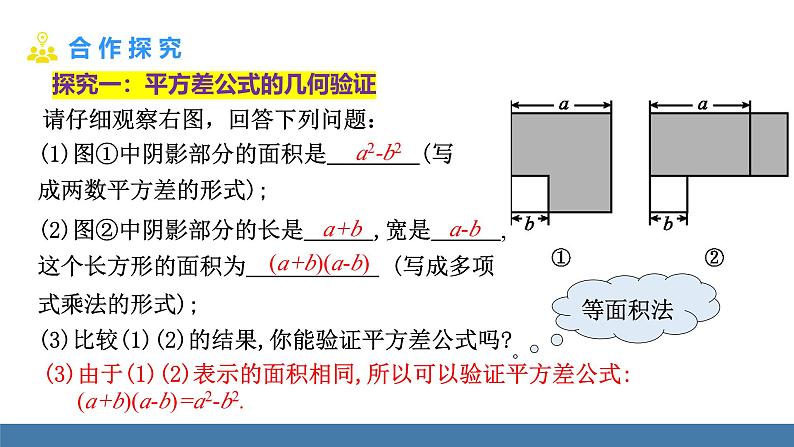
请仔细观察右图,回答下列问题:
探究一:平方差公式的几何验证
(3)比较(1)(2)的结果,你能验证平方差公式吗?
(3)由于(1)(2)表示的面积相同,所以可以验证平方差公式: (a+b)(a-b)=a2-b2.
(1)图①中阴影部分的面积是 (写成两数平方差的形式); (2)图②中阴影部分的长是 ,宽是 ,这个长方形的面积为 (写成多项式乘法的形式);
探究二:平方差公式的应用
63 143 639964 144 6400
用含字母a的式子表示这一规律,可写成 .
(a-1)(a+1)=a2-1
应用平方差公式(a+b)(a−b)=a2−b2即可说明以上规律的正确性.
(1)计算下列各式,并观察他们的共同特点:
7×9= ,11×13= ,79×81= ,8×8= ,12×12= ,80×80= .
(2)从以上的过程中,你发现了什么规律?
(3)请用字母表示这一规律,你能说明它的正确性吗?
例1 用平方差公式进行计算:(1)103×97;(2)118×122.
解:103×97 =(100+3)(100-3) =1002-32 =9991.
解:118×122 =(120-2)(120+2) =1202-22 =14396.
运用平方差公式计算两数乘积时,关键是找到这两个数的平均数,再将原数与这个平均数进行比较,变成两数的和与差的积的形式.
例2 计算:(1)a2(a+b)(a-b)+a2b2;(2)(2x-5)(2x+5)-2x(2x-3).
解:(1)a2(a+b)(a-b)+a2b2=a2(a2-b2)+a2b2=a4-a2b2+a2b2=a4.
(2)(2x-5)(2x+5)-2x(2x-3)=(2x)2-52-(4x2-6x)=4x2-25-4x2+6x=6x-25.
1.用平方差公式进行计算:(1)9.8×10.2;(2)49×51;
解:(1)原式=(10-0.2)×(10+0.2) =102-0.22 =100-0.04 =99.96.
(2)49×51 =(50-1)(50+1) =502-12 =2499.
2. 计算:20242-2023×2025.
解:20242-2023×2025 =20242-(2024-1)(2024+1) =20242-(20242-1) =20242-20242+1 =1.
3.已知a=7202,b=721×719;则( ) A.a=b B.a>b C.a
相关课件
这是一份数学北师大版(2024)3 乘法公式说课ppt课件,共17页。
这是一份初中数学北师大版(2024)七年级下册(2024)3 乘法公式课文内容课件ppt,共21页。PPT课件主要包含了a2−b2,平方差,右边是这两项的平方差,由以上计算可得,a+b2,a-b2,ba-b,a2+2ab+b2,a2-2ab+b2,完全平方公式等内容,欢迎下载使用。
这是一份初中数学北师大版(2024)七年级下册(2024)3 乘法公式评课ppt课件,共21页。PPT课件主要包含了每一项,面积变了吗,相等吗,x2-22,12-3a2,x2-5y2,2y2-z2,平方差公式,-x2,-32-a2等内容,欢迎下载使用。










