中考数学复习讲义：第三章 三角形 模型（十）——双角平分线模型（含解析）

这是一份中考数学复习讲义：第三章 三角形 模型（十）——双角平分线模型（含解析），共9页。
典例秒杀

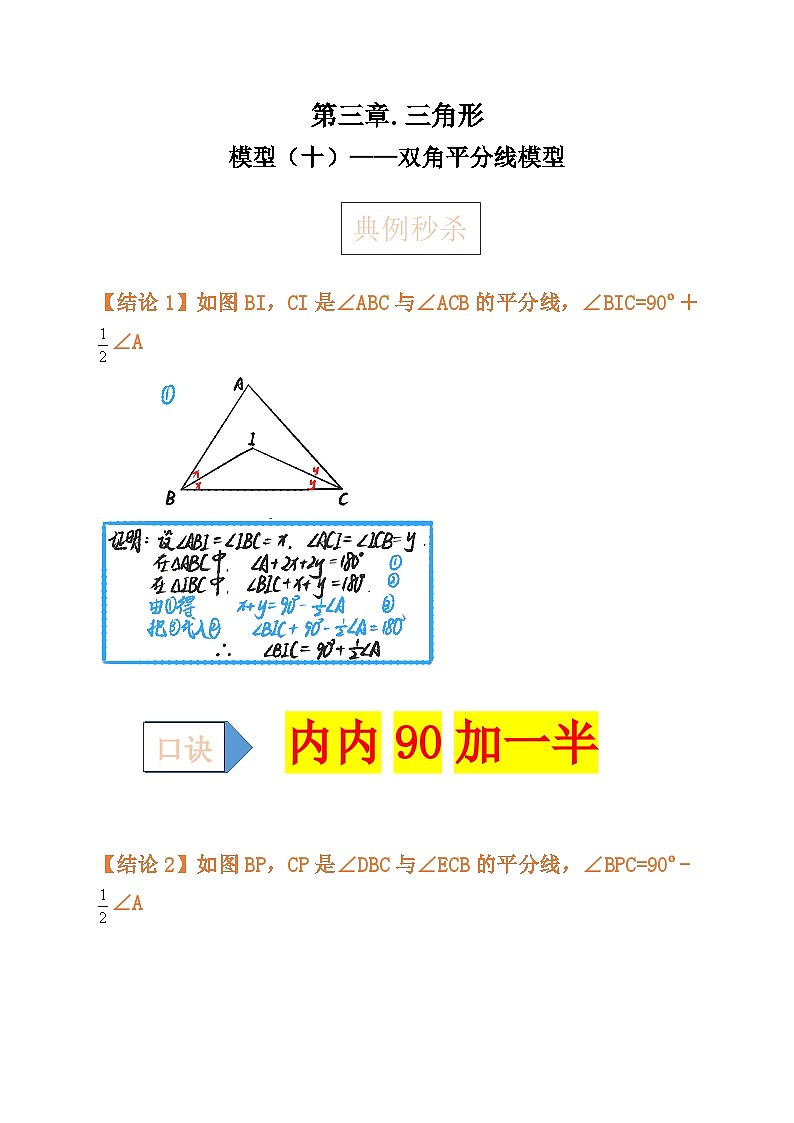
【结论1】如图BI，CI是∠ABC与∠ACB的平分线，∠BIC=90º＋∠A

内内90加一半
口诀

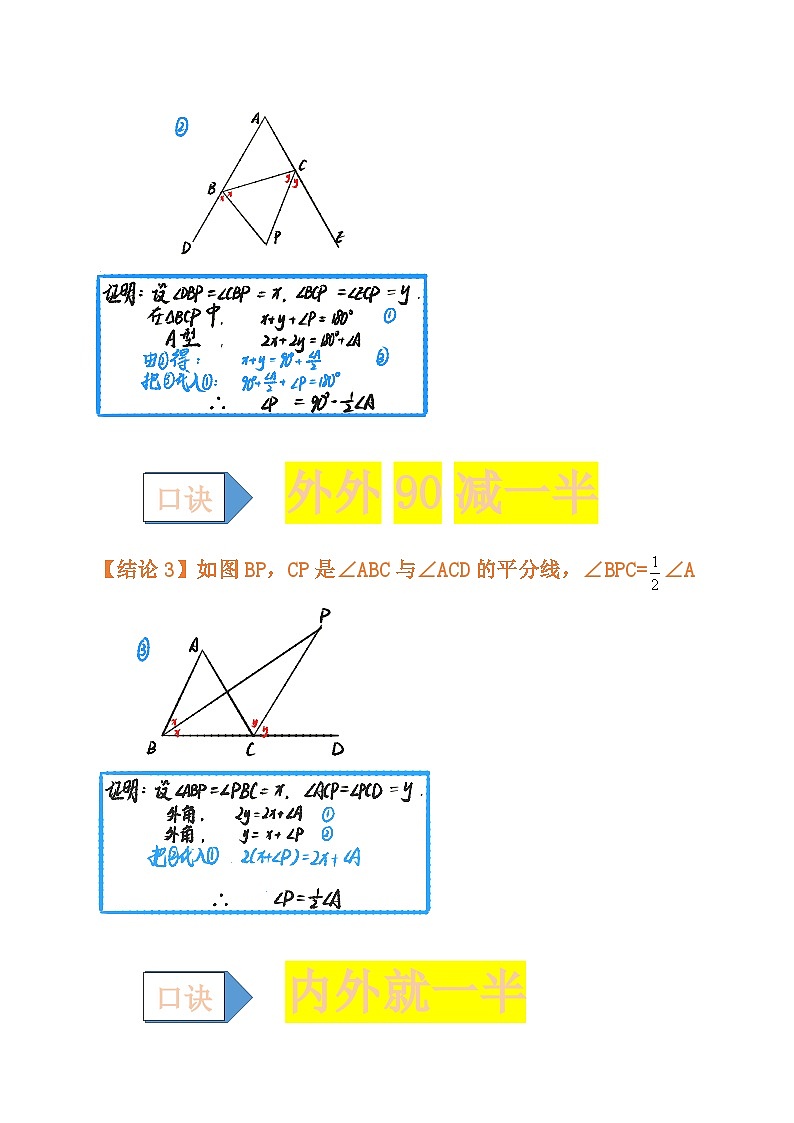
【结论2】如图BP，CP是∠DBC与∠ECB的平分线，∠BPC=90º-∠A

外外90减一半
口诀

【结论3】如图BP，CP是∠ABC与∠ACD的平分线，∠BPC=∠A

内外就一半
口诀

典例秒杀
典例1 ☆☆☆☆☆
1.如图，在△ABC中，∠ABC 和∠ACB的平分线相交于点O，若∠BAC=80°，则∠BOC 的度数是（ ）
A.130° B.120° C.100° D. 90°
【答案】A
【解析】∵BO，CO是△ABC的内角平分线，由“内内 90°加一半”得，
∠BOC=90°+∠BAC=90°+×80°=130°.
故选 A.
典例2 ☆☆☆☆☆
如图，BA1和 CA1分别是△ABC的内角平分线和外角平分线，BA1是∠A1BD的平分线，CA2是∠A1CD的平分线，BA3是∠A2BD平分线，CA3是∠A2CD的平分线，……以此类推，若∠A=α，则∠ A2020=__________。

【答案】
【解析】∵BA1，为△ABC的内角平分线，CA1为△ABC的外角平分线，
由“内外就一半”得，∠A₁ =∠A=·α
同理，∠A₂= ∠A₁=·α
∠A₃=∠A₂=·α
……
∠ A2020=
典例3 ☆☆☆☆☆
【问题】如图1，在△ABC中，BE平分∠ABC，CE平分∠ACB，若∠A=80°，
则∠BEC=________；若∠A= n°，则∠BEC=___________。
【探究】（1）如图 2，在△ABC中，BD，BE三等分∠ABC，CD，CE 三等分∠ACB，若∠A=nº，则∠BEC=_________。
⑵如图3，O是∠ABC的平分线 BO 与∠ACD 的平分线 CO 的交点，试分析∠BOC 和∠A 有怎样的关系，并说明理由；
⑶如图4，O是△ ABC 的外角∠DBC与∠BCE 的平分线BO和CO的交点，则∠BOC与∠A 有怎样的关系?（只写结论不需要证明）

【解析】【问题】130°，90°+n°
【探究】（1）由三角形内角和定理，得∠ABC+∠ACB=180°-∠A= 180°- n°.
∵BD，BE三等分∠ABC，CD，CE三等分∠ACB，
∴∠EBC=∠ABC，∠ECB=∠ACB
∴∠EBC+∠ECB=(∠ABC+∠ACB)=×(180°- n°）=120º-n°
∴∠BEC=180°-(∠EBC＋∠ECB)=180°-(120°-n°）=60º＋n°
∠BOC=∠A，理由如下∶
由三角形的外角性质，得∠ACD=∠A＋∠ABC，∠OCD=∠BOC+∠OBC.
∵O是∠ABC 的平分线 BO 与∠ACD的平分线 CO 的交点，
∴∠ABC=2∠OBC,∠ACD=2∠OCD,
∴∠A+∠ABC=2(∠BOC+∠OBC)=2 ∠BOC,
∴∠BOC=∠A
（3）∠BOC=90°-∠A

小试牛刀
1.（★★★☆☆）如图所示，在△ABC中，∠ABC，∠ACB的平分线 BE，CD相交于点F，若∠A=60°，则∠BFC等于（ ）
A.121° B. 120° C.119° D. 118°
2.（★★★☆☆）如图，五边形 ABCDE在∠BCD，∠EDC处的外角分别是∠FCD，∠GDC，CP，DP分别平分∠FCD 和∠GDC且相交于点P.若∠A=160°，∠B=80°，∠E=90°，则∠CPD=_________。


直击中考
1.如图，在△ABC中，BE是∠ABC的平分线，CE 是∠ACM 的平分线，BE 与 CE 相交于点E.若 ∠A= 60°，则∠BEC 的度数为（ ）
A.15° B.30° C.45° D.60°

双角平分线模型不仅可以帮助同学们秒杀选填问题，而且在复杂约几何解答题中也能快速理清角度之间的关系，进而解决问题﹒
第三章.三角形
模型（十）——双角平分线模型
答案：
小试牛刀
答案 B
解析 ：∵BE，CD均为△ABC的内角平分线，
∴由“内内9０º加－半”，得∠BFC＝9０º＋∠A=90º+×60º=120º
故选Ｂ．
答案 105º
解析：如图，延长BF，EG交于点H

在△CDH 中，CP，DP分别平分∠HCD和∠HDC，
∴由“内内9０º加一半”，得∠CPD＝９０º＋∠H
又∠A＋∠B＋∠H ＋∠E=360º,
∴∠H =360º-160º-80º-90º= 30º
∴∠CPD=90°+×30°=105°
直击中考
答案 B
解析: ∵BE 为△ABC的内角平分线， CE为△ABC的外角平分线，
∴“由内外就一半”，得∠BEC=∠A=×60°=30°.
故选 B.