课时作业30 空间几何体平行关系-2024-2025学年高考数学艺体生一轮复习课时作业

这是一份课时作业30 空间几何体平行关系-2024-2025学年高考数学艺体生一轮复习课时作业，文件包含课时作业30空间几何体平行关系教师版docx、课时作业30空间几何体平行关系学生版docx等2份试卷配套教学资源，其中试卷共19页， 欢迎下载使用。
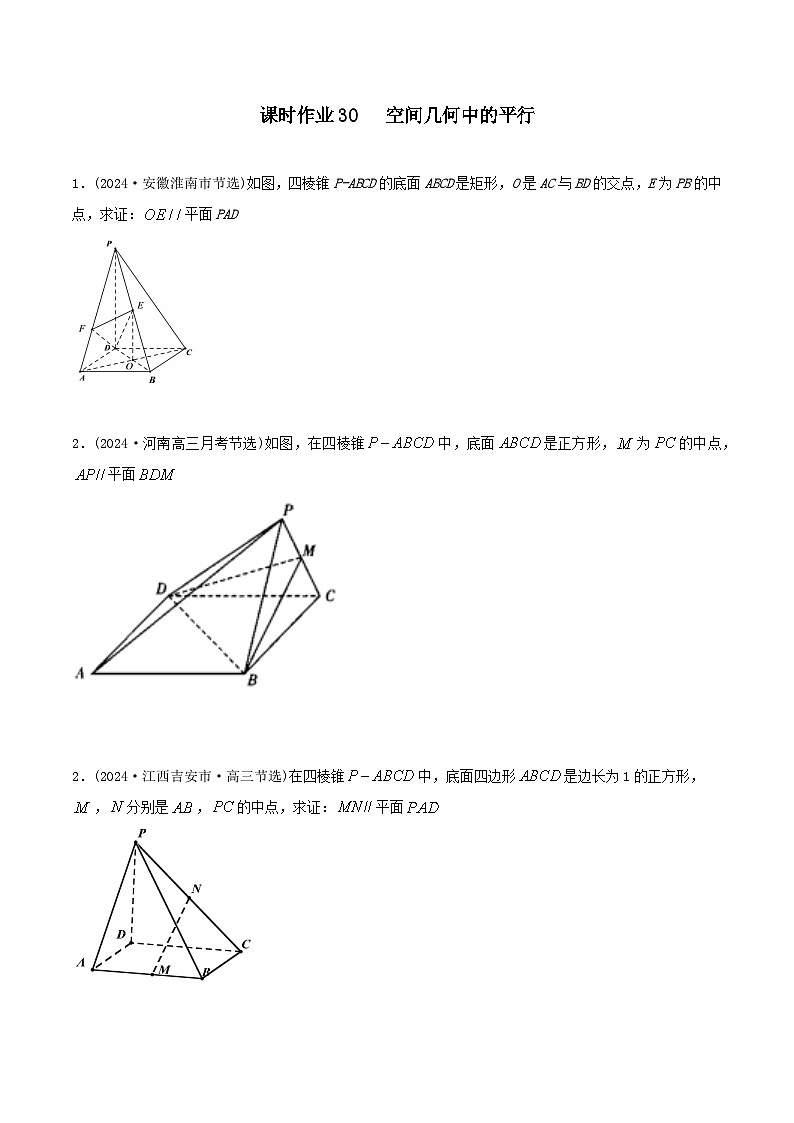
1．(2024·安徽淮南市节选)如图，四棱锥P-ABCD的底面ABCD是矩形，O是AC与BD的交点，E为PB的中点，求证：平面PAD
【答案】证明见解析
【解析】因为四边形是矩形，所以是的中点
又是的中点，所以
因为平面，平面所以平面．
2．(2024·河南高三月考节选)如图，在四棱锥中，底面是正方形，为的中点，平面
【答案】证明见解析
【解析】连接交于，连接，则为中点，
所以为的中位线，所以，
又因为平面，平面，所以平面．
2．(2024·江西吉安市·高三节选)在四棱锥中，底面四边形是边长为1的正方形，，分别是，的中点，求证：平面
【答案】证明见解析
【解析】取的中点，连结、，
∵是的中点，∴，且，
∵底面四边形是边长是１的正方形，又是的中点，
∴，且∴，
∴，且，∴四边形是平行四边形，
∴，又磁面，平面，∴平面.
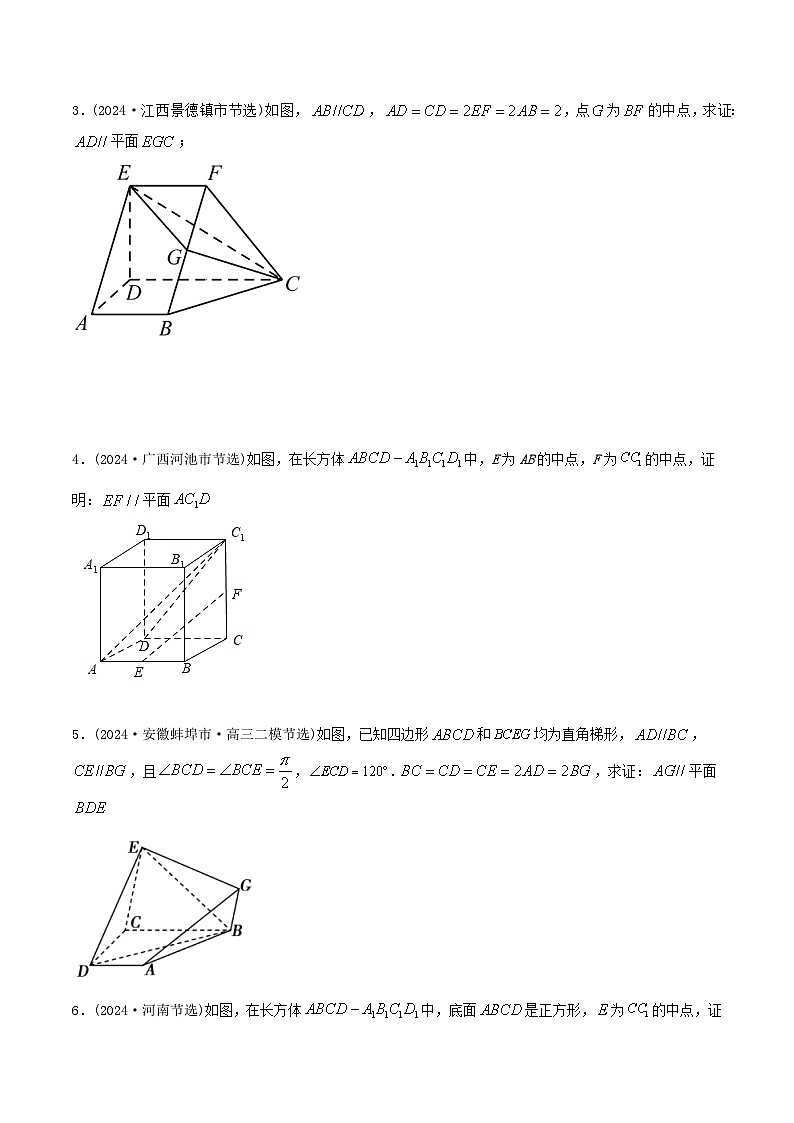
3．(2024·江西景德镇市节选)如图，，，点为的中点，求证：平面；
【答案】证明见解析
【解析】证明：取中点，连接交于点，可知点 为的中点，在三角形中，又因 ，可得，平面， 平面，所以平面
4．(2024·广西河池市节选)如图，在长方体中，E为AB的中点，F为的中点，证明：平面
【答案】证明见解析
【解析】证明：取的中点G，连GF，AG，如图所示：
∵G为的中点，F为的中点，∴且，
∵E为AB的中点，，，∴且
∴四边行AEFG为平行四边形，
∴，又平面，平面，∴平面.
5．(2024·安徽蚌埠市·高三二模节选)如图，已知四边形和均为直角梯形，，，且，.，求证：平面
【答案】证明见解析
【解析】证明：在平面中，过作于，交于，连，
由题意知，，且，
∵，，
故四边形为平行四边形，∴，
又平面，平面，故平面.
6．(2024·河南节选)如图，在长方体中，底面是正方形，为的中点，证明：平面
【答案】证明见解析
【解析】证明：设，连接，则是中点，又是中点，
∴，又平面，平面，∴平面．
7．(2024·河南驻马店市·高三期末节选)如图，该多面体由底面为正方形的直四棱柱被截面所截而成，其中正方形的边长为，是线段上(不含端点)的动点，，证明：平面；
【答案】证明见解析
【解析】证明：取的中点，连接，．
因为该多面体由底面为正方形的直四棱柱被截面所截而成，
所以截面是平行四边形，
则．
因为，
所以，且，
所以四边形是平行四边形，所以．
因为平面，平面，
所以平面．
8．(2024·山西运城市·高三期末节选)如图，在几何体中，四边形为等腰梯形，且，，四边形为矩形，且，M，N分别为，的中点，求证：平面
【答案】证明见解析
【解析】证明：取的中点Q，连接，，
则，且
又，且 ，所以且，
所以四边形为平行四边形，所以，
又因为平面，平面，
所以平面
9．(2024·安徽黄山市节选)已知四棱锥中，，设平面平面，求证：
【答案】证明见解析
【解析】证明：因为，平面，平面，所以平面.
因为平面，平面平面，所以.
10．(2024·江苏苏州市节选)如图所示，在四棱锥中，底面是正方形，对角线与交于点，点在棱上，若平面，求的值;
【答案】1
【解析】连结，
∵平面，平面，平面平面，∴．
∵底面是正方形，为中点，∴是的中位线，则．
11．(2024·安徽六安市·高三一模节选)如图，在四棱锥中，，，E是PD的中点，证明：平面PBC
【答案】证明见解析
【解析】证明：取PC的中点F，连接EF、BF，如图所示：
因为E、F分别为PD，PC的中点，所以且，
又，，所以且
所以四边形是平行四边形，所以，
又因为平面PBC，平面PBC所以平面PBC．
12．(2024·浙江台州市·高三期末节选)如图，在三梭柱中，为的中点，求证：平面
【答案】证明见解析
【解析】连结，与交于点，连结，
四边形是平行四边形，为中点，
为中点，得，又平面，故平面；
13．(2024·江西高三其他模拟节选)如图，已知四边形为菱形，对角线与相交于O，，平面平面直线，求证：
【答案】证明见解析
【解析】因为四边形为菱形，所以，
平面，平面平面，
因为平面平面直线平面，所以；
14．(2024·全国高三专题练习)如图，在正方体ABCD­A1B1C1D1中，S是B1D1的中点，E，F，G分别是BC，DC，SC的中点，求证：
(1)直线EG平面BDD1B1；
(2)平面EFG平面BDD1B1.
【答案】(1)证明见解析；(2)证明见解析.
【解析】证明：(1)如图，连接SB，因为E，G分别是BC，SC的中点，
所以EGSB.
又因为SB平面BDD1B1，EG平面BDD1B1，
所以直线EG平面BDD1B1.
(2)连接SD，因为F，G分别是DC，SC的中点，
所以FGSD.
又因为SD平面BDD1B1，FG平面BDD1B1，
所以FG平面BDD1B1，
由(1)有直线EG平面BDD1B1；
又EG平面EFG，FG平面EFG，EG∩FG=G，
所以平面EFG平面BDD1B1.
15.(2024·全国高三专题练习)如图，在四棱锥中，为的中点，在上，且，，证明：平面
【答案】证明见解析
【解析】取的中点，连接､，则∵为的中点，
∴，且，
又，∴，且，
∴，且，∴四边形为平行四边形，∴，
又∵平面，平面，∴平面；
16.(2024·贵溪市第一中学节选)已知四边形为梯形，，对角线、交于点，平面，，，为线段上的点，，证明：平面；
【答案】证明见解析
【解析】证明：，，
在梯形中，，则梯形为等腰梯形，
，，
由余弦定，得，，
，整可得，解得，
，，，
又平面，平面，平面
备战高考数学成套的一轮复习，二轮复习，专题高分突破，考前回归，模拟试卷尽在备战高考QQ群722859698也可联系微信fjshuxue加入夸克网盘群3T一线老师必备资料一键转存自动更新永不过期